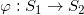追忆清华逝水年华 (之一)
公元2018年9月16日,清华大学计算机科学与技术系建系六十周年系庆,"贵系"1989级同学入学29周年纪念,将近三十年。往日如昨,那一年青春年少,英姿勃发,高举理想主义的大旗,一路高...
追忆清华逝水年华 (之二、之三)
人文教育清华本科的人文教育非常丰富,令我们受益终身。 哲学 哲学吴卓老师思想深刻,词锋犀利,桀骜不驯,人格独立。课上教导大家不要被主流所裹挟,要躬身体悟,深刻思考。多年之后...
超材料设计中的共形几何
依随三维打印技术的推广成熟,增材制造工艺的日益普及,超材料设计的理论和方法蓬勃发展。超材料(meta-material)指的是自然界中所没有的一类具有特殊性质的人造材料。这类材料具有特异的光、...
《计算共形几何》教程第一章
【最近老顾等人合著的汉语教程《计算共形几何》已经完成初稿。这里我们将第一章公布,其他章节会在清华暑期课程中讲授。希望大家批评指正,不吝赐教。有兴趣预定者,请联系gu@cmsa.fas.harvard....
深度学习的几何理解(2) – 学习能力的上限
(最近,哈佛大学丘成桐先生领导的团队,大连理工大学罗钟铉教授、雷娜教授领导的团队应用几何方法研究深度学习。老顾受邀在一些大学和科研机构做了题为“深度学习的几何观点”的报告,汇报了这...
深度学习的几何理解(3) – 概率变换的几何观点
(最近,哈佛大学丘成桐先生领导的团队,大连理工大学罗钟铉教授、雷娜教授领导的团队应用几何方法研究深度学习。老顾受邀在一些大学和科研机构做了题为“深度学习的几何观点”的报告,汇报了这...
虚构的对抗,GAN with the wind
在过去的两三年中,对抗生成网络(Generative Adersarial Network GAN)获得了爆炸式的增长,其应用范围几乎涵盖了图像处理和机器视觉的绝大多数领域。其精妙独到的构思,令人拍案叫绝;其绚烂...
清华笔记:计算共形几何讲义 (2)代数拓扑
这次课程,我们简单介绍曲面基本群(一维同伦群)的理论梗概。主要概念有基本群的定义,表示,计算。然后我们介绍覆盖空间理论,特别是万有覆盖空间理论,曲线同伦检测算法。【1】给出了课程的...
清华笔记:计算共形几何讲义 (4)单纯同调
这次课程,我们介绍单纯同调理论。在代数拓扑中,有单纯同调、奇异同调和de Rham同调理论。它们所用的数学工具不同,但是理论彼此等价。【1】给出了本课程的视频链接。 基本方法代数...
清华笔记:计算共形几何讲义 (6)上同调的霍奇理论
这次课程,我们介绍霍奇分解定理,这一定理在图形学、视觉和网络中,应用非常广泛。直观而言,我们考察曲面上的切向量场,如果这个向量场光滑得无以复加,那么这个向量场被称为是调和场(harmon...
清华笔记:计算共形几何讲义 (7)矢量场设计
漫长的课程至此,我们终于可以应用所学的理论工具来分析解决一些实际问题了。我们学习了曲面的代数拓扑和 微分拓扑,de Rham上同调的霍奇理论,作为应用实例,我们讨论如何构造曲面上光滑矢量场...
清华笔记:计算共形几何讲义 (8)狭缝映射(Slit Map)的存在性
我们用较为初等的复变函数方法证明一种共形映射的存在性:狭缝映射(slit mapping)。如图所示,给定亏过为0的多连通曲面,存在共形映射将其映射到平面区域,每个边界的联通分支都被映成一条狭...