OpenCasCade官方开发文档翻译(3)–occt建模数据

介绍

建模数据提供数据结构来表示 2D 和 3D 几何模型。

本手册解释了如何使用建模数据。

几何实用程序

Geometry Utilities 提供以下服务：

• 通过插值和近似创建形状
• 直接构造形状
• 曲线和曲面到 BSpline 曲线和曲面的转换
• 计算 2D 和 3D 曲线上点的坐标
• 计算形状之间的极值。

插值和近似

在建模中，经常需要将点近似或插值成曲线和曲面。在插值中，当曲线或曲面通过所有点时，过程完成；近似地，当它尽可能接近这些点时。

曲线和曲面的近似将 2D 和 3D 几何中使用的各种函数组合在一起，用于：

• 使用 2D BSpline 或 Bezier 曲线对一组 2D 点进行插值；
• 使用 2D BSpline 或 Bezier 曲线逼近一组 2D 点；
• 使用 3D BSpline 或 Bezier 曲线或 BSpline 曲面对一组 3D 点进行插值；
• 使用 3D BSpline 或 Bezier 曲线或 BSpline 曲面逼近一组 3D 点。

您可以通过两种方式对近似值进行编程：

• 使用高级函数，旨在提供一种通过最少编程获得近似值的简单方法，
• 使用低级函数，专为需要更多控制近似值的用户而设计。

一组点分析

GProp包中的PEquation类允许分析点的集合或云，并验证它们在给定精度内是否重合、共线或共面。如果是，则算法计算这些点的平均点、平均线或平均平面。如果不是，则算法计算包含所有点的最小框。

基本插值和逼近

包Geom2dAPI和GeomAPI提供了简单的近似和插值方法，只需最少的编程

2D 插值

Geom2dAPI包中的Interpolate类允许构建受约束的 2D BSpline 曲线，由曲线通过的点表定义。如果需要，可以为表中的每个点给出切线的参数值和向量。

3D 插值

GeomAPI包中的Interpolate类允许构建受约束的 3D BSpline 曲线，由曲线通过的点表定义。如果需要，可以为表中的每个点给出切线的参数值和向量。

此类可以按如下方式实例化：

从这个对象，可以按如下方式请求 BSpline 曲线：

2D 近似

Geom2dAPI包中的PointsToBSpline类允许构建 2DBSpline 曲线，它近似于一组点。您必须定义曲线的最低和最高度数、它的连续性以及它的公差值。公差值用于检查点彼此之间是否不太接近，或者切向矢量是否不太小。生成的 BSpline 曲线将是 C2 或二阶连续曲线，除非在曲线通过的点上定义了相切约束。在这种情况下，它只会是 C1 连续的。

3D 近似

GeomAPI包中的PointsToBSpline类允许构建 3D BSplinecurve，它近似于一组点。有必要定义曲线的最低和最高阶数、其连续性和公差。容差值用于检查点之间是否不太接近，或者切向量是否太小。

生成的 BSpline 曲线将是 C2 或二阶连续曲线，除非在曲线通过的点上定义了相切约束。在这种情况下，它将只有 C1 连续。此类实例化如下：

从这个对象，可以按如下方式请求 BSpline 曲线：

曲面逼近

GeomAPI包中的PointsToBSplineSurface类允许构建 BSpline 曲面，该曲面近似或内插一组点。

高级近似

包AppDef和A​​ppParCurves提供低级函数，允许对近似值进行更多控制。

低级函数提供了第二个 API，该 API 具有以下功能：

• 为近似值定义强制切线。这些切线有起点和终点。
• 平行近似一组曲线以尊重相同的参数化。
• 平滑近似。这是为了产生一个流线型的曲线。

您还可以找到要计算的函数：

• 包含一组点的最小框
• 一组共面、共线或重合点的平均平面、直线或点。

多点约束逼近

AppDef包提供了低级工具，允许使用多点约束将点组平行逼近为 Bezier 或 B-Spline 曲线。

提供以下低级服务：

• 点约束数组的定义：MultiLine
  类允许定义给定数量的多点约束，以构建多线，多线穿过有序的多点约束。

  

  使用多点约束定义多线

  在这张图片中：

  • Pi, Qi, Ri … Si can be 2D or 3D points.
  • 定义为一个组：Pn , Qn , Rn, … Sn形成一个 MultipointConstraint。它们具有相同的通道、相切和曲率约束。
  • P1、P2、 … Pn或Q、R、 … 或S系列表示要近似的线。
• 一组点约束的定义：MultiPointConstraint
  类允许定义一个多点约束并计算一组点到几条曲线的近似值。
• 从一组点计算贝塞尔曲线的近似值：Compute
  类允许将一组点近似为贝塞尔曲线。
• 从一组点计算 BSpline 曲线的近似值：BSplineCompute类
  允许将一组点近似为 BSpline 曲线。
• 变分准则的定义：TheVariational
  类允许使用最小二乘法结合变分准则（通常是每个约束点的权重）将近似曲线平滑到给定数量的点。

通过参数或几何约束进行逼近

AppParCurves包提供了低级工具，以允许将点组平行逼近为具有参数或几何约束的 Bezier 或 B-Spline 曲线，例如要求曲线通过给定点，或具有给定的切线或曲率一个特定的点。

使用的算法包括：

• 最小二乘法
• 在给定公差值内寻找最佳近似值。

提供以下低级服务：

• 索引与对象
  的关联：类ConstraintCouple允许您将索引与对象关联，以使用AppDef_TheVariational计算流线型曲线。
• 贝塞尔曲线的一组近似值的定义：MultiCurve
  类允许定义由多条贝塞尔曲线组成的多线的近似值。
• BSpline 曲线的一组近似值的定义：MultiBSpCurve类
  允许定义由多个 BSpline 曲线组成的多线的近似值。
• 定义构成一组点约束的点MultiPoint
  类允许定义构成多线的 2D 或 3D 点组。

示例：如何逼近一条关于切线的曲线

要相对于切线近似曲线，请执行以下步骤：

1. 从要逼近的点集创建AppDef_MultiPointConstraints类型的对象，并使用方法SetTang设置相切向量。
2. 从AppDef_MultiPointConstraint创建一个AppDef_MultiLine类型的对象。
3. 使用AppDef_BSplineCompute实例化Approx_BSplineComputeLine来执行近似。

直接构造

来自gce、GC和GCE2d包的直接构造方法提供了简化的算法来构建基本的几何实体，例如直线、圆和曲线。它们补充了gp、Geom和Geom2d包提供的参考定义。

由gce、GCE2d和GC包实现的算法很简单：不会创建由高级位置约束定义的对象（有关此主题的更多信息，请参阅Geom2dGcc和GccAna，它们通过约束描述几何）。

例如，要使用gp包从一个点和一个半径构造一个圆，需要在创建圆之前构造轴Ax2d 。如果使用gce包，并以Ox为轴，则可以直接从一个点和一个半径创建一个圆。

另一个例子是gce_MakeCirc类，它提供了一个框架，用于定义圆的几何构造中遇到的八个问题并实现八种相关的构造算法。

创建（或实现）的对象是一种算法，可以查询以找出，特别是：

• 它的结果是gp_Circ，并且
• 它的状态。这里，状态表示构建是否成功。

如果不成功，状态会给出失败的原因。

此外，gce、GCE2d和GC各有一个Root类。这个类是包中所有类的根，它们返回一个状态。返回的状态（成功构造或构造错误）由枚举gce_ErrorType描述。

请注意，构造几何变换的类不会返回状态，因此不会从Root继承。

简单几何实体

以下用于从gp包构建实体的算法由gce包提供。

• 与另一条平行的二维线在一定距离处，
• 与另一条平行的二维线穿过一个点，
• 通过两点的二维圆，
• 在一定距离处平行于另一个的二维圆，
• 平行于另一个通过一点的二维圆，
• 通过三个点的二维圆，
• 从一个中心和一个半径的二维圆，
• 来自五点的二维双曲线，
• 一个中心和两个顶点的二维双曲线，
• 五点的二维椭圆，
• 一个中心和两个顶点的二维椭圆，
• 三点的二维抛物线，
• 从中心和顶点的二维抛物线，
• 与另一条平行的线通过一个点，
• 通过两点的线，
• 与另一个通过一点同轴的圆，
• 在给定距离处与另一个同轴的圆，
• 通过三个点的圆，
• 圆心、半径和垂直于平面，
• 以轴为圆（中心+法线），
• 中心和两个顶点的双曲线，
• 椭圆的中心和两个顶点，
• 平面经过三点，
• 平面偏离其正常水平，
• 在给定距离处平行于另一个平面的平面，
• 平行于另一个通过一点的平面，
• 来自点数组的平面，
• 从给定轴和给定半径的圆柱体，
• 圆形底座的圆柱体，
• 三点气缸，
• 在给定距离处平行于另一个圆柱体的圆柱体，
• 平行于通过一点的另一个圆柱体的圆柱体，
• 四个点的锥体，
• 来自给定轴和两个通过点的锥体，
• 来自两个点（一个轴）和两个半径的圆锥，
• 在给定距离处平行于另一个锥体，
• 平行于另一个通过一点的锥体，
• 所有变换（旋转、平移、镜像、缩放变换等）。

gp包中的每个类，如Circ、Circ2d、Mirror、Mirror2d等，都有对应的gce包中的MakeCirc、MakeCirc2d、MakeMirror、MakeMirror2d等类。

可以使用gce包类创建一个点，然后对其进行查询以恢复相应的gp对象。

如果您不确定参数是否可以在不引发异常的情况下创建gp对象，这将很有用。在上述情况下，如果Point1和Point2比MakeLin2d要求的公差值更接近，则函数Status将返回枚举gce_ConfusedPoint。这告诉你为什么不能创建gp对象。如果知道Point1和Point2点之间的距离超过了公差值，那么可以直接创建gp对象，如下：

句柄操作的几何实体

GC和GCE2d包提供了用于从Geom和Geom2D包构建实体的算法实现。它们实现与gce包相同的算法，并且还包含用于修剪曲面和曲线的算法。可以使用以下算法：

• 由两点修剪的圆弧，
• 由两个参数修剪的圆弧，
• 由一个点和一个参数修剪的圆弧，
• 由两点修剪的椭圆的椭圆弧，
• 由两个参数修剪的椭圆的椭圆弧，
• 由一个点和一个参数修剪的椭圆的椭圆弧，
• 由两点修剪的抛物线形成的抛物线弧，
• 由两个参数修剪的抛物线的抛物线弧，
• 由一个点和一个参数修剪的抛物线的抛物线弧，
• 由两点修剪的双曲线的双曲线弧，
• 由两个参数修剪的双曲线的双曲线弧，
• 由一个点和一个参数修剪的双曲线的双曲线弧，
• 从两点开始的线段，
• 来自两个参数的线段，
• 来自一个点和一个参数的线段，
• 从圆形底座和高度修剪圆柱体，
• 从三个点修剪圆柱体，
• 从轴、半径和高度修剪圆柱体，
• 从四个点修剪圆锥，
• 从两个点（一个轴）和一个半径修剪圆锥，
• 从两个同轴圆修剪锥。

GCE2d包中的每个类，如Circle、Ellipse、Mirror等，都有对应 Geom2d 包中的MakeCircle 、MakeEllipse、MakeMirror等类。此外，MakeArcOfCircle 类从Geom2d返回一个 TrimmedCurve 类型的对象。

GC包中的每个类，如Circle、Ellipse、Mirror等，都有Geom包中对应的MakeCircle、MakeEllipse、MakeMirror等类。以下类从Geom返回TrimmedCurve类型的对象：

• MakeArcOfCircle
• MakeArcOfEllipse
• MakeArcOfHyperbola
• MakeArcOfParabola
• MakeSegment

与 BSplines 之间的转换

BSplines 组件之间的转换有两个不同的目的：

• 首先，它提供了一个均匀的公式，可以用来描述任何曲线或曲面。这对于为单个数据结构模型编写算法很有用。BSpline 公式可用于表示由描述几何数据结构的组件（“基本几何类型”、“2D 几何类型”和“3D 几何类型”组件）提供的最基本几何对象。
• 其次，它可用于将 BSpline 曲线或曲面划分为一系列曲线或曲面，从而提供更高程度的连续性。这对于编写需要在应用它们的对象中具有特定程度的连续性的算法很有用。不连续性仅位于对象的边界上。

“与 BSplines 之间的转换”组件由三个包组成。

Convert包提供了将以下内容转换为 BSpline 曲线或曲面的算法：

• 基于gp包中的基本 2D 曲线（直线、圆形或圆锥曲线）的有界曲线，
• 基于gp包中的基本曲面（圆柱、圆锥、球体或圆环）的有界曲面，
• 一系列由其极点定义的相邻 2D 或 3D 贝塞尔曲线。

这些算法计算定义生成的 BSpline 曲线或曲面所需的数据。然后，这些基本数据（度数、周期特征、极点和权重、节点和多重性）可以直接用于算法中，或者可以通过调用Geom2d_BSplineCurve、Geom_BSplineCurve或Geom_BSplineSurface。

Geom2dConvert包提供以下内容：

• 一个全局函数，用于从基于 Geom2d 包中的 2D 曲线的有界曲线构造 BSpline 曲线，
• 一种分裂算法，计算应切割 2D BSpline 曲线的点，以获得具有相同连续性的弧，
• 用于构造由该分割算法或其他类型的 BSpline 曲线分割创建的 BSpline 曲线的全局函数，
• 一种将二维 BSpline 曲线转换为一系列相邻贝塞尔曲线的算法，
• 一种将任意二维曲线转换为一系列相邻二维圆弧和二维直线段的算法。

GeomConvert包还提供以下内容：

• 一个全局函数，用于从基于 Geom 包中的曲线的有界曲线构造 BSpline 曲线，
• 一种分裂算法，它计算应该切割 BSpline 曲线的点，以获得具有相同连续性的弧，
• 用于构造由该分割算法或其他类型的 BSpline 曲线分割创建的 BSpline 曲线的全局函数，
• 一种算法，将 BSpline 曲线转换为一系列相邻的 Bezier 曲线，
• 一个全局函数，用于根据 Geom 包中的曲面从有界曲面构造 BSpline 曲面，
• 一种分割算法，它确定 BSpline 曲面应沿其切割的曲线，以获得具有相同连续性程度的补丁，
• 用于构造由该分割算法或其他类型的 BSpline 曲面分割创建的 BSpline 曲面的全局函数，
• 一种算法，将 BSpline 曲面转换为一系列相邻的 Bezier 曲面，
• 一种算法，将相邻贝塞尔曲面的网格转换为 BSpline 曲面。
• 将 NURBS、Bezier 和其他一般参数化曲线和曲面转换为分析曲线和曲面的算法。

曲线上的点

曲线上的点组件包含高级函数，为计算 2D 或 3D 曲线上的点的复杂算法提供 API。

3d 空间中的参数化曲线上存在以下特征点：

• 曲线上等距的点，
• 沿等弦曲线分布的点，
• 与曲线上另一点相距给定距离的点。

GCPnts包提供了计算这些点的算法：

• AbscissaPoint计算曲线上距曲线上另一个点给定距离的点。
• UniformAbscissa计算曲线上给定横坐标处的一组点。
• UniformDeflection计算在曲线和由计算点产生的多边形之间的最大恒定偏转处的一组点。

示例：可视化曲线。

让我们采用一条适应曲线C，即一个对象，它是由 Geom2d 包中的 2D 曲线（在 Adaptor_Curve2d 曲线的情况下）或 Geom 包中的 3D 曲线（在 Adaptor_Curve 的情况下）提供的服务之间的接口曲线），以及计算算法在曲线上所需的服务。调整后的曲线按以下方式创建：

二维案例：

3D案例​​：

然后用这个对象构造算法：

极端

GeomAPI和Geom2dAPI包提供了用于计算 2d 和 3d 中点、曲线和曲面之间最小距离的类。

这些包计算之间距离的极值：

• 点和曲线，
• 点和面，
• 两条曲线，
• 曲线和曲面，
• 两个表面。

点与曲线/曲面之间的极值

GeomAPI_ProjectPointOnCurve类允许计算点和曲线之间的所有极值。极值是与曲线正交的线段的长度。GeomAPI_ProjectPointOnSurface类允许计算点和曲面之间的所有极值。极值是与表面正交的线段的长度。这些类使用“投影”标准进行优化。

曲线间极值

Geom2dAPI_ExtremaCurveCurve类允许计算两条2D 几何曲线之间的所有最小距离。GeomAPI_ExtremaCurveCurve类允许计算两条3D 几何曲线之间的所有最小距离。这些类使用欧几里得距离作为优化标准。

曲线和曲面之间的极值

GeomAPI_ExtremaCurveSurface类允许计算 3D 曲线和曲面之间的一个极值。极值是与曲线和曲面正交的线段的长度。此类使用“投影”标准进行优化。

曲面之间的极值

GeomAPI_ExtremaSurfaceSurface类允许计算两个表面之间的一个最小距离和一个最大距离。此类使用欧几里得距离来计算最小值，并使用“投影”标准来计算最大值。

二维几何

Geom2d包在 2dspace 中定义几何对象。所有几何实体都经过 STEP 处理。对象通过引用处理。

特别是，Geom2d包提供了以下类：

• 点、向量和曲线的描述，
• 它们使用坐标系在平面中的定位，
• 它们的几何变换，通过应用平移、旋转、对称、缩放变换及其组合。

以下对象可用：

• 观点，
• 笛卡尔点，
• 向量，
• 方向，
• 具有幅度的矢量，
• 轴，
• 曲线，
• 线，
• 圆锥：圆、椭圆、双曲线、抛物线、
• 圆角曲线：修剪曲线、NURBS 曲线、Bezier 曲线、
• 偏移曲线。

在创建几何对象之前，有必要决定如何处理对象。Geom2d包提供的对象是按引用而不是按值处理的。复制一个实例会复制句柄，而不是对象，因此对一个实例的更改会反映在它的每次出现中。如果需要一组对象实例而不是单个对象实例，则可以使用TColGeom2d包。这个包为来自Geom2d包的曲线提供标准和常用的一维数组和序列的实例化。所有对象都有两个版本：

• 通过引用处理和
• 按值处理。

Geom2d曲线的关键特征是它们是参数化的。每个类都提供函数来处理曲线的参数方程，特别是计算曲线上参数 u 的点以及在该点处的 1、2..、N 阶导数向量。

作为参数化的结果，Geom2d曲线是自然定向的。

参数化和方向将基本Geom2d曲线与gp包提供的等效曲线区分开来。Geom2d包提供了将Geom2d对象转换为gp对象的转换函数，反之亦然，如果可能的话。

此外，Geom2d包提供了更复杂的曲线，包括贝塞尔曲线、BSpline 曲线、修剪曲线和偏移曲线。

Geom2d对象根据多个级别的继承结构进行组织。

因此，椭圆（具体类Geom2d_Ellipse）也是圆锥曲线，继承自抽象类Geom2d_Conic，而贝塞尔曲线（具体类Geom2d_BezierCurve）也是有界曲线，继承自抽象类Geom2d_BoundedCurve；这两个例子也是曲线（抽象类Geom2d_Curve）。曲线、点和向量从抽象类Geom2d_Geometry继承，它描述了Geom2d包中任何几何对象的共有属性。

这种继承结构是开放的，并且可以描述从Geom2d包中提供的对象继承的新对象，前提是它们尊重它们要继承的类的行为。

最后，Geom2d对象可以在更复杂的数据结构中共享。例如，这就是为什么它们在拓扑数据结构中使用的原因。

Geom2d包使用gp包的服务来：

• 实施初等代数微积分和基本解析几何，
• 描述可应用于Geom2d对象的几何变换，
• 描述Geom2d对象的基本数据结构。

然而，Geom2d包本质上是提供数据结构而不是算法。您可以参考GCE2d包以找到更多针对Geom2d对象的演进构造算法。

3D 几何

Geom包定义了 3d 空间中的几何对象，包含了所有基本的几何变换，如恒等、旋转、平移、镜像、比例变换、变换组合等，以及依赖于几何对象的参考定义的特殊功能（例如在 B 样条曲线上添加控制点、修改曲线等）。所有几何实体都经过 STEP 处理。

特别是，它提供了以下类：

• 点、向量、曲线和曲面的描述，
• 使用轴或坐标系在 3D 空间中定位，以及
• 它们的几何变换，通过应用平移、旋转、对称、缩放变换及其组合。

以下对象可用：

• 观点
• 笛卡尔点
• 向量
• 方向
• 带大小的向量
• 轴
• 曲线
• 线
• 圆锥曲线：圆、椭圆、双曲线、抛物线
• 偏移曲线
• 基本面：平面、圆柱体、圆锥体、球体、圆环面
• 有界曲线：修剪曲线、NURBS 曲线、Bezier 曲线
• 有界曲面：矩形修剪曲面、NURBS曲面、Bezier曲面
• 扫掠曲面：直线挤压曲面、旋转曲面
• 偏移曲面。

Geom曲线和曲面的关键特征是它们是参数化的。每个类都提供函数来处理曲线或曲面的参数方程，特别是计算：

• 曲线上参数 u 的点，或
• 参数 (u, v) 在曲面上的点。与此时的 1、2、…N 阶导数向量一起。

作为这种参数化的结果，几何曲线或曲面是自然定向的。

参数化和方向将基本 Geom 曲线和曲面与gp包中相同（或相似）名称的类区分开来。Geom包还提供了将 Geom 对象转换为gp对象的转换函数，反之亦然，当这种转换是可能的时。

此外，Geom包提供了更复杂的曲线和曲面，包括：

• Bezier 和 BSpline 曲线和曲面，
• 扫掠表面，例如旋转表面和线性挤压表面，
• 修剪过的曲线和曲面，以及
• 偏移曲线和曲面。

Geom 对象根据多个级别的继承结构进行组织。因此，球体（具体类Geom_SphericalSurface）也是基本曲面，继承自抽象类Geom_ElementarySurface，而贝塞尔曲面（具体类Geom_BezierSurface）也是有界曲面，继承自抽象类Geom_BoundedSurface；这两个例子也是表面（抽象类Geom_Surface）。曲线、点和向量从抽象类Geom_Geometry继承，它描述了Geom包中任何几何对象的共有属性。

这种继承结构是开放的，并且可以描述从 Geom 包中提供的对象继承的新对象，条件是它们尊重它们要继承的类的行为。

最后，Geom 对象可以在更复杂的数据结构中共享。例如，这就是为什么它们在拓扑数据结构中使用的原因。

如果需要一组对象实例而不是单个对象实例，则可以使用TColGeom包。此包提供Geom包中曲线的一维和二维数组和序列的实例化。所有对象都有两个版本：

• 通过引用处理和
• 按值处理。

Geom包使用gp包的服务来：

• 实施初等代数微积分和基本解析几何，
• 描述可应用于 Geom 对象的几何变换，
• 描述 Geom 对象的基本数据结构。

然而，Geom 包本质上是提供数据结构，而不是算法。

您可以参考GC包来找到更多针对 Geom 对象的进化构造算法。

拓扑

OCCT 拓扑允许访问和操作对象的数据，而无需处理它们的 2D 或 3D 表示。OCCT 几何根据坐标或参数值提供对象的描述，而拓扑则描述参数空间中对象的数据结构。这些描述使用了该空间的部分位置和限制。

拓扑库允许您构建纯拓扑数据结构。拓扑定义简单几何实体之间的关系。通过这种方式，您可以将复杂形状建模为更简单实体的组件。由于内置的​​非流形（或混合维度）功能，您可以构建混合模型：

• 0D实体，例如点；
• 一维实体，例如曲线；
• 2D 实体，例如曲面；
• 3D 实体，例如体积。

例如，您可以表示由多个不同实体组成的单个对象，这些实体包含连接或不连接到外部边界的嵌入曲线和曲面。

抽象拓扑数据结构描述了一个基本实体——一个形状，它可以分为以下组件拓扑：

• 顶点——与几何中的点相对应的零维形状；
• 边——对应于曲线的形状，并在每个末端由一个顶点限制；
• 连线——由顶点连接的一系列边；
• 面——由闭合线包围的平面（在 2D 几何中）或表面（在 3D 几何中）的一部分；
• 壳 – 由其线边界的某些边缘连接的面的集合；
• 实体 – 由外壳限制的 3D 空间的一部分；
• 复合固体——固体的集合。

线和实体可以是无限的或封闭的。

具有 3D 底层几何图形的面也可以指代近似底层表面的连接三角形的集合。表面可以是未定义的，只留下由三角形表示的面。如果是这样，该模型是纯粹的多面体。

拓扑定义了简单几何实体之间的关系，因此可以将它们链接在一起以表示复杂的形状。

抽象拓扑由六个包提供。前三个包描述了 Open CASCADE 技术中使用的拓扑数据结构：

• TopAbs包为拓扑驱动的应用程序提供通用资源。它包含用于描述基本拓扑概念的枚举：拓扑形状、方向和状态。它还提供了管理这些枚举的方法。
• TopLoc包提供了处理 3D 局部坐标系的资源：Datum3D和Location。Datum3D描述了一个基本坐标系，而Location包含一系列基本坐标系。
• TopoDS包描述了用于建模和构建纯拓扑数据结构的类。

三个额外的包提供了访问和操作这个抽象拓扑的工具：

• TopTools包提供了用于拓扑数据结构的基本工具。
• TopExp包提供类来探索和操作TopoDS包中描述的拓扑数据结构。
• BRepTools 包提供类来探索、操作、读取和写入 BRep 数据结构。这些更复杂的数据结构将拓扑描述与附加几何信息相结合，并包括用于评估同一对象（例如，点）的不同可能表示的等价性的规则。

形状内容

TopAbs包提供了描述拓扑基本概念的通用枚举以及处理这些枚举的方法。它不包含任何类。这个包已经与拓扑的其余部分分开，因为它包含的概念足够通用，可以被所有拓扑工具使用。这通过保持独立于建模资源来避免重新定义枚举。TopAbs包定义了三个概念：

• 类型– TopAbs_ShapeEnum；
• 方向– TopAbs_Orientation；
• 状态– StateTopAbs_State。

拓扑类型

TopAbs包含TopAbs_ShapeEnum枚举，它列出了不同的拓扑类型：

• COMPOUND – 一组任何类型的拓扑对象。
• COMPSOLID – 复合实体是一组通过面连接的实体。它将 WIRE 和 SHELL 的概念扩展到实体。
• SOLID——受壳限制的空间的一部分。它是三维的。
• SHELL – 一组通过边缘连接的面。外壳可以打开或关闭。
• FACE——在 2D 中，它是平面的一部分；在 3D 中，它是表面的一部分。它的几何形状受轮廓约束（修剪）。它是二维的。
• WIRE – 一组由其顶点连接的边。它可以是开放或封闭的轮廓，具体取决于边是否链接。
• EDGE——对应于约束曲线的拓扑元素。一条边通常受顶点限制。它有一个维度。
• VERTEX – 对应于点的拓扑元素。它的维度为零。
• 形状——涵盖上述所有内容的通用术语。

拓扑模型可以被认为是具有邻接关系的对象图。在 2D 或 3D 空间中对零件进行建模时，它必须属于 ShapeEnum 枚举中列出的类别之一。TopAbspackage 列出了可以在任何模型中找到的所有对象。它不能扩展，但可以使用一个子集。例如，实体的概念在 2D 中是没有用的。

枚举项按从最复杂到最简单的顺序出现，因为对象可以在其描述中包含更简单的对象。例如，一个面引用它的线、边和顶点。

方向

方向的概念由TopAbs_Orientation枚举表示。方向是在各种建模者中发现的方向感的广义概念。这在形状限制几何域时使用；并且与边界的概念密切相关。三种情况如下：

• 受顶点限制的曲线。
• 受边缘限制的表面。
• 空间受限于一张面。

在每种情况下，用作高维几何域边界的拓扑形式定义了两个局部区域，其中一个被任意视为默认区域。

对于由顶点限制的曲线，默认区域是参数大于顶点的点集。也就是说它是沿曲线自然方向的顶点之后的曲线部分。

对于由边缘限制的表面，默认区域位于边缘的左侧，遵循其自然方向。更准确地说，它是由曲面的法线向量和与曲线相切的向量的向量积所指向的区域。

对于受面限制的空间，默认区域位于曲面法线的负侧。

基于此默认区域，方向允许保留要保留的区域的定义，称为内部或材料。有四个方向定义内部。

方向	描述
FORWARD	内部是默认区域。
REVERSED	内部是与默认互补的区域。
INTERNAL	内部包括两个区域。边界位于材料内部。例如，实体内部的表面。
EXTERNAL	内部不包括任何区域。边界位于材料之外。例如线框模型中的边。

方向的概念是一个非常普遍的概念，它可以用于出现区域或边界的任何上下文中。因此，例如，当描述边缘和轮廓的相交时，不仅可以描述相交的顶点，而且可以描述边缘如何将其视为边界与轮廓相交。因此，边缘将分为两个区域：外部和内部，相交顶点将是边界。因此，方向可以与交点相关联，如下图所示：

方向	联想
FORWARD	进入
REVERSED	退出
INTERNAL	从里面摸
EXTERNAL	从外面摸

除了 Orientation 枚举，TopAbs包还定义了四种方法：

状态

TopAbs_State枚举描述了一个顶点或一组顶点相对于一个区域的位置。有四个术语：

位置	描述
IN	重点是内部。
OUT	重点是外部。
ON	该点在边界上（在公差范围内）。
UNKNOWN	点的状态是不确定的。

引入了 UNKNOWN 术语是因为此枚举通常用于表示计算结果，计算结果可能会失败。当无法知道一个点是在里面还是在外面时，可以使用这个术语，这是开放线或面的情况。

State 枚举也可用于指定对象的各个部分。下图显示了与面相交的边的部分。

形状位置

可以将局部坐标系视为以下任意一种：

• 具有原点和三个正交向量的右手三面体。gp_Ax2包对应于这个定义。
• +1 行列式的变换，允许局部和全局参考框架之间的坐标变换。这对应于gp_Trsf。

TopLoc包区分了两个概念：

• TopLoc_Datum3D类提供基本参考坐标，由右手正交坐标系或右手酉变换表示。
• TopLoc_Location类提供由基本坐标组成的复合参考坐标。它是由一系列对基本标记的引用组成的标记。存储产生的累积变换以避免重新计算整个列表的变换总和。

如果两个参考坐标由相同的基本坐标以相同的顺序组成，则它们是相等的。没有数值比较。因此，如果两个坐标不是从相同的基本坐标构建的，则它们可以对应于相同的变换而不相等。

例如，考虑三个基本坐标：

复合坐标为：

注意C3 和 C4 是相等的，因为它们都是 R1 * R2 * R3。

TopLoc包主要针对拓扑数据结构，但也可以用于其他目的。

坐标变化

TopLoc_Datum3D类表示基本坐标的变化。必须共享此类更改，以便此类继承自Standard_Transient。坐标由变换gp_Trsfpackage表示。此转换没有缩放因子。

操作形状和子形状

TopoDS包描述了具有以下特征的拓扑数据结构：

• 参考一个既没有方向也没有位置的抽象形状。
• 通过工具类访问数据结构。

如上所述，OCCT 拓扑描述了参数空间中对象的数据结构。这些描述使用了该空间部分的定位和限制。可以用这些术语描述的形状类型是顶点、面和形状。顶点是根据参数空间中的定位来定义的，而面部和形状是根据该空间的限制来定义的。

OCCT 拓扑描述还允许将这些术语中定义的简单形状组合成集合。例如，一组边形成一条线；一组面形成壳，一组实体形成复合实体（Open CASCADE Technology 中的 CompSolid）。您还可以将任何一种形状组合成化合物。最后，您可以为形状指定方向和位置。

按照从顶点到复合实体的复杂性顺序列出形状，将我们引向数据结构的概念，即如何将形状分解为一组更简单的形状。这其实就是TopoDS包的目的。

形状的模型是一种可共享的数据结构，因为它可以被其他形状使用（一条边可以被实体的多个面使用）。一个可共享的数据结构是通过引用来处理的。当简单的参考不足时，会添加两条信息：方向和局部坐标参考。

• 方向说明如何在边界中使用引用的形状（来自TopAbs的方向）。
• 局部参考坐标（来自TopLoc的Location）允许在不同于其定义的位置引用形状。

TopoDS_TShape类是所有形状描述的根。它包含一个形状列表。如有必要，继承TopoDS_TShape的类可以携带几何域的描述（例如，与 TVertex 关联的几何点）。TopoDS_TShape是在其定义参考框架中对形状的描述。此类通过引用进行操作。

TopoDS_Shape类描述了对形状的引用。它包含对底层抽象形状、方向和局部参考坐标的引用。这个类是由值操作的，因此不能被共享。

代表底层抽象形状的类永远不会被直接引用。TopoDS_Shape类总是用来指​​代它。

每个形状的特定信息（几何支持）总是通过继承添加到派生自TopoDS_TShape的类中。下图显示了由通过边连接的两个面形成的壳示例。

在上图中，壳由底层形状 TS 描述，面由 TF1 和 TF2 描述。从 TE1 到 TE7 有 7 条边，从 TV1 到 TV6 有 6 个顶点。

线 TW1 参考从 TE1 到 TE4 的边；TW2 参考从 TE4 到 TE7。

顶点被边引用如下：TE1(TV1,TV4), TE2(TV1,TV2), TE3(TV2,TV3), TE4(TV3,TV4), TE5(TV4,TV5), TE6(T5,TV6) ),TE7(TV3,TV6)。

请注意，此数据结构不包含任何反向引用。所有参考都从更复杂的基础形状到不太复杂的形状。用于访问信息的技术将在后面描述。数据结构尽可能紧凑。子对象可以在不同对象之间共享。

两个非常相似的对象，可能是同一对象的两个版本，可能共享相同的子对象。数据结构中局部坐标的使用允许共享重复子结构的描述。

紧凑的数据结构避免了与复制操作相关的信息丢失，复制操作通常用于创建对象的新版本或应用坐标更改时。

下图显示了一个包含两个版本的实体的数据结构。第二个版本展示了一系列在不同位置钻孔的相同孔。数据结构紧凑，但保留了子元素的所有信息。

从TSh2 到底层面 TFCyl的三个参考具有相关的局部坐标系，它们对应于孔的连续位置。

继承 TopoDS_Shape 的类

TopoDS基于类TopoDS_Shape和定义其基础形状的类。这有一定的优势，但主要的缺点是这些类过于笼统。它们可以表示的不同形状不会键入它们（顶点、边等），因此不可能引入检查以避免不连贯性，例如在边中插入面。

TopoDS包提供了两组类，一组继承了既没有方向也没有位置的底层形状，另一组继承了TopoDS_Shape ，它们代表了TopAbs包中枚举的标准拓扑形状

以下类继承 Shape ：TopoDS_Vertex、TopoDS_Edge、TopoDS_Wire、TopoDS_Face、TopoDS_Shell、TopoDS_Solid、TopoDS_CompSolid和TopoDS_Compound 。尽管名称与继承自TopoDS_TShape的名称相似，但它们的使用方式却存在巨大差异。

TopoDS_Shape类及其继承的类是操作拓扑对象的自然手段。TopoDS_TShape类是隐藏的。TopoDS_TShape在其原始局部坐标系中描述一个类，没有方向。TopoDS_Shape是对TopoDS_TShape的引用，具有方向和局部参考。

TopoDS_TShape类被推迟；TopoDS_Shape类不是。使用TopoDS_Shape类允许在不知道其类型的情况下操作拓扑对象。它是一种通用形式。纯拓扑算法经常使用TopoDS_Shape类。

TopoDS_TShape类通过引用进行操作；TopoDS_Shape按值分类。TopoDS_Shape只不过是通过方向和局部坐标增强的参考。TopoDS_Shapes的分享是没有意义的。重要的是底层TopoDS_TShapes的共享。参数中的赋值或段落不会复制数据结构：这只会创建新的TopoDS_Shapes引用相同的TopoDS_TShape。

尽管继承TopoDS_TShape的类用于添加额外信息，但不应在从TopoDS_Shape继承的类中添加额外字段。从TopoDS_Shape继承的类仅用于专门化引用，以便从静态类型控制（由编译器执行）中受益。例如，在参数中接收TopoDS_Face的例程对于编译器来说比接收 TopoDS_Shape 的例程更精确。除了在TopoDS中找到的类之外，派生其他类是没有意义的。对拓扑数据结构的所有引用都是使用TopoDS中定义的 Shape 类及其继承者进行的。

从TopoDS_Shape类继承的类没有构造函数，否则类型控制将通过隐式转换消失（C++ 的一个特性）。TopoDS包提供包方法，用于在这些子类之一中转换 TopoDS_Shape 类的对象，并进行类型验证。

以下示例显示了一个例程接收TopoDS_Shape类型的参数，然后将其放入变量 V（如果它是顶点）或调用方法 ProcessEdge（如果它是边）。

拓扑数据结构探索

TopExp包提供了用于探索使用 TopoDS 包描述的数据结构的工具。探索拓扑结构意味着查找给定类型的所有子对象，例如，查找实体的所有面。

TopExp包提供类TopExp_Explorer来查找给定类型的所有子对象。资源管理器由以下内容构建：

• 要探索的形状。
• 要查找的形状类型，例如 VERTEX、EDGE，但 SHAPE 除外，这是不允许的。
• 要避免的形状类型。例如外壳、边缘。默认情况下，此类型为 SHAPE。此默认值意味着对探索没有限制。

资源管理器访问整个结构，以便找到不包含在要避免的类型中的请求类型的形状。下面的示例显示了如何查找形状S中的所有面：

找出所有不在边上的顶点

找到一个 SHELL 中的所有面，然后找到所有不在一个 SHELL 中的面：

Explorer 假定对象仅包含相同或劣等类型的对象。例如，如果搜索面，它不会查看线、边或顶点来查看它们是否包含面。

TopExp包中的MapShapes方法允许填充地图。如果对象被多次引用，则使用 E​​xplorer 类的探索可以多次访问该对象。例如，实体的边线通常由两个面引用。要只处理一次对象，必须将它们放置在 Map 中。

例子

在以下示例中，对象的所有面和所有边都根据以下规则绘制：

• 面由具有FaceIsoColor颜色的NbIso等参数线网络表示。
• 边以一种颜色绘制，表示共享边的面数：
  • FreeEdgeColor用于不属于面的边缘（即线框元素）。
  • 属于单个面的边的BorderEdgeColor 。
  • SharedEdgeColor用于属于多个面的边。
• DrawEdge和DrawFaceIso方法也可用于显示单个边和面。

执行以下步骤：

1. 将边缘存储在地图中并并行创建整数数组以计算共享边缘的面数。这个数组被初始化为零。
2. 探索面孔。每张面都画出来了。
3. 探索边缘并为每个边缘增加数组中面的计数器。
4. 从边缘地图中，使用与面数相对应的颜色绘制每条边缘。

形状列表和map

TopTools包包含用于利用TopoDS数据结构的工具。它是TCollection包中工具的实例化，带有TopoDS的 Shape 类。

• TopTools_Array1OfShape, HArray1OfShape –使用TopoDS_Shape实例化NCollection_Array1。
• TopTools_SequenceOfShape –使用TopoDS_Shape实例化NCollection_Sequence。
• TopTools_MapOfShape – NCollection_Map的实例化。允许构造形状集。
• TopTools_IndexedMapOfShape – NCollection_IndexedMap的实例化。允许构建形状表和其他数据结构。

使用TopTools_Map，可以保留一组对 Shapes 的引用而不会重复。以下示例将数据结构的大小计算为TShapes的数量。

如果数据结构中存在共享，则此程序不正确。

因此，对于四个边的轮廓，它应该计算 1 条线 + 4 条边 +4 个顶点，结果为 9，但由于每个顶点都由两条边共享，因此该程序将返回 13。一种解决方案是将所有形状放在地图中以免计算两次，如下例所示：

注意有关 Maps 的更多详细信息，请参阅TCollection文档（基础类参考手册）。

下面的例子更加雄心勃勃，它编写了一个使用IndexedMap复制数据结构的程序。副本是一个相同的结构，但它与原件没有任何共同之处。主要算法如下：

• 结构中的所有形状都放入IndexedMap中。
• 与地图并行创建一个 Shapes 表以接收副本。
• 使用辅助递归函数复制结构，该函数从映射复制到数组。

在上面的示例中，索引i是未在 Map 中处理的第一个对象的索引。当i达到与 Map 相同的大小时，这意味着所有内容都已处理。处理包括在 Map 中插入所有子对象，如果它们还没有在 Map 中，则使用大于i的索引插入它们。

请注意，插入对象时带有设置为标识和正向方向的局部参考。只有底层的 TShape 非常有趣。

下面是辅助函数，它将秩为i的元素从地图复制到表中。此方法检查对象是否已被复制；如果没有复制，则在表中执行一个空副本，并通过在地图中找到它们的排名来插入所有子元素的副本。

线浏览

BRepTools_WireExplorer类可以按照连接顺序访问线的边缘。

例如，在图像中的线中，我们希望按 {e1, e2, e3,e4, e5} 的顺序恢复边缘：

然而， TopExp_Explorer以任何顺序恢复行。

形状的属性

形状的局部属性

BRepLProp包提供形状的局部属性组件，其中包含计算 BRep 模型中边和面的各种局部属性的算法。

可以查询的本地属性有：

• 对于支持边的曲线上的参数 u 点：
  • 重点，
  • 导数向量，直到三次，
  • 切线向量，
  • 正常的，
  • 曲率和曲率中心；
• 对于支持面的表面上的参数 (u, v) 点：
  • 重点，
  • 导数向量，直到二阶，
  • u 和 v 等参曲线的切线向量，
  • 法线向量，
  • 最小或最大曲率，以及相应的曲率方向；
• 支持一条边的曲线的连续性程度，由其他两条边在它们的连接点连接而成。

分析的边和面被描述为BRepAdaptor曲线和曲面，它们为形状提供了用于描述其几何支持的接口。局部属性的基点由其在曲线上的 u 参数值或在曲面上的 (u, v) 参数值定义。

曲线和曲面的局部属性

“曲线和曲面的局部属性”组件提供了用于计算几何曲线（在 2D 或 3D 空间中）或曲面上的各种局部属性的算法。它由以下部分组成：

• Geom2dLProp包，它允许计算二维曲线上参数点的导数和切线向量（法线和曲率）；
• GeomLProp包，提供 3D 曲线和曲面的局部属性；
• LProp包，它提供了一个用于表征二维曲线上特定点的枚举。

曲线是Geom_Curve曲线（在 3D 空间中）或Geom2d_Curve曲线（在平面中）。曲面是Geom_Surface曲面。计算局部属性的点由曲线上的 u 参数值和曲面上的 (u,v) 参数值定义。

可以查询与上述点相同的局部属性，另外还可以查询 2D 曲线：

• 对应于最小或最大曲率的点；
• 拐点。

示例：如何检查表面凹度

要检查表面的凹度，请执行以下操作：

1. 对曲面进行采样并计算每个点的高斯曲率。
2. 如果曲率的值改变符号，表面是凹的还是凸的取决于视点。
3. 要计算高斯曲率，请使用 GeomLProp 中的 SLprops 类，它从LProp实例化通用类SLProps并使用GaussianCurvature方法。

曲线和曲面的连续性

GeomAbs_Shape枚举中描述了曲线和曲面支持的连续性类型。

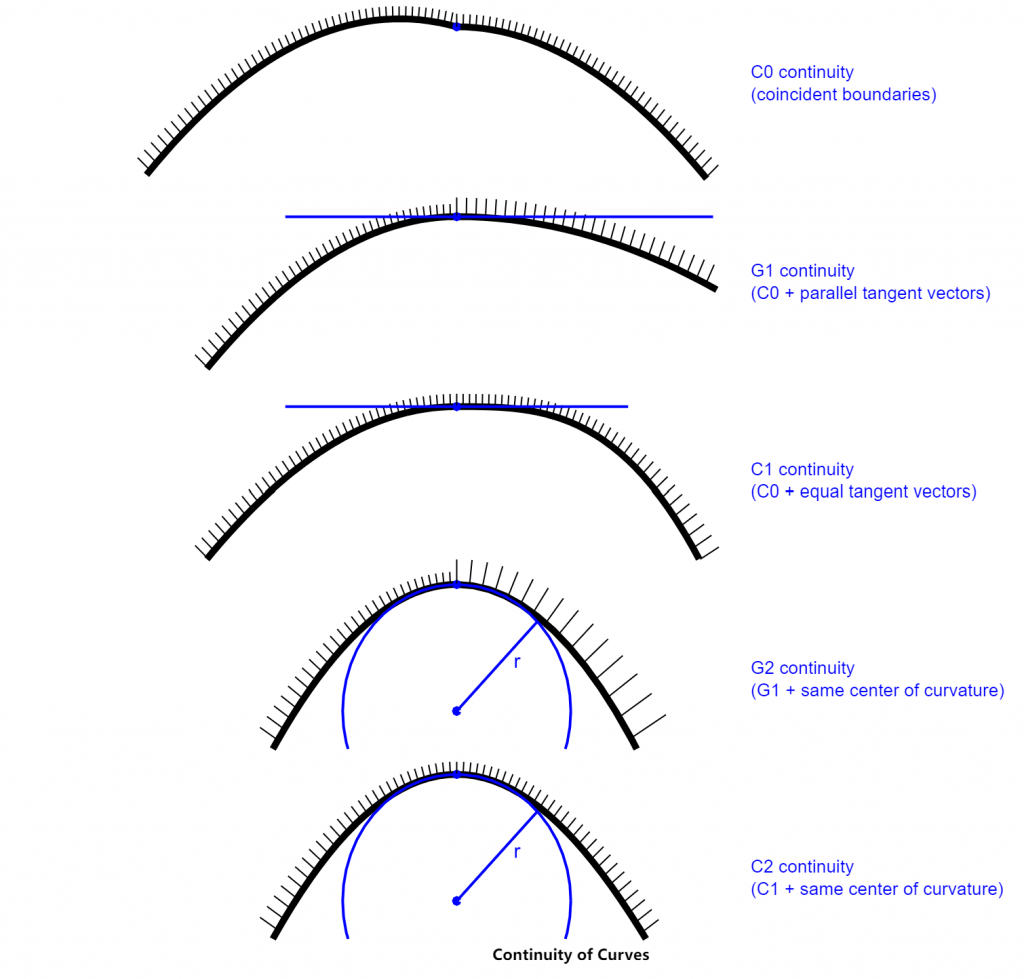
对于曲线，支持以下类型的连续性（见下图）：

• C0 ( GeomAbs_C0 ) – 参数连续性。与 G0（几何连续性）相同，所以最后一个不单独变量表示。
• G1 ( GeomAbs_G1 ) – 左右切线向量是平行的。
• C1 ( GeomAbs_C1 ) – 表示一阶导数的连续性。
• G2 ( GeomAbs_G2 ) – 除了 G1 连续性之外，左右曲率中心相同。
• C2 ( GeomAbs_C2 ) – 所有导数的连续性直到二阶。
• C3 ( GeomAbs_C3 ) – 所有导数的连续性直到三阶。
• CN ( GeomAbs_CN ) – 所有导数的连续性直到 N 阶（连续性的无限阶）。

注意：几何连续性（G1，G2）意味着曲线可以重新参数化以具有参数（C1，C2）连续性。

支持以下类型的表面连续性：

• C0 ( GeomAbs_C0 ) – 参数连续性（表面没有不连续点或曲线）。
• G1 ( GeomAbs_G1 ) – 表面在每个点都有一个切平面。
• C1 ( GeomAbs_C1 ) – 表示一阶导数的连续性。
• G2 ( GeomAbs_G2 ) – 除了 G1 连续性之外，主曲率和方向也是连续的。
• C2 ( GeomAbs_C2 ) – 所有导数的连续性直到二阶。
• C3 ( GeomAbs_C3 ) – 所有导数的连续性直到三阶。
• CN ( GeomAbs_CN ) – 所有导数的连续性直到 N 阶（连续性的无限阶）。

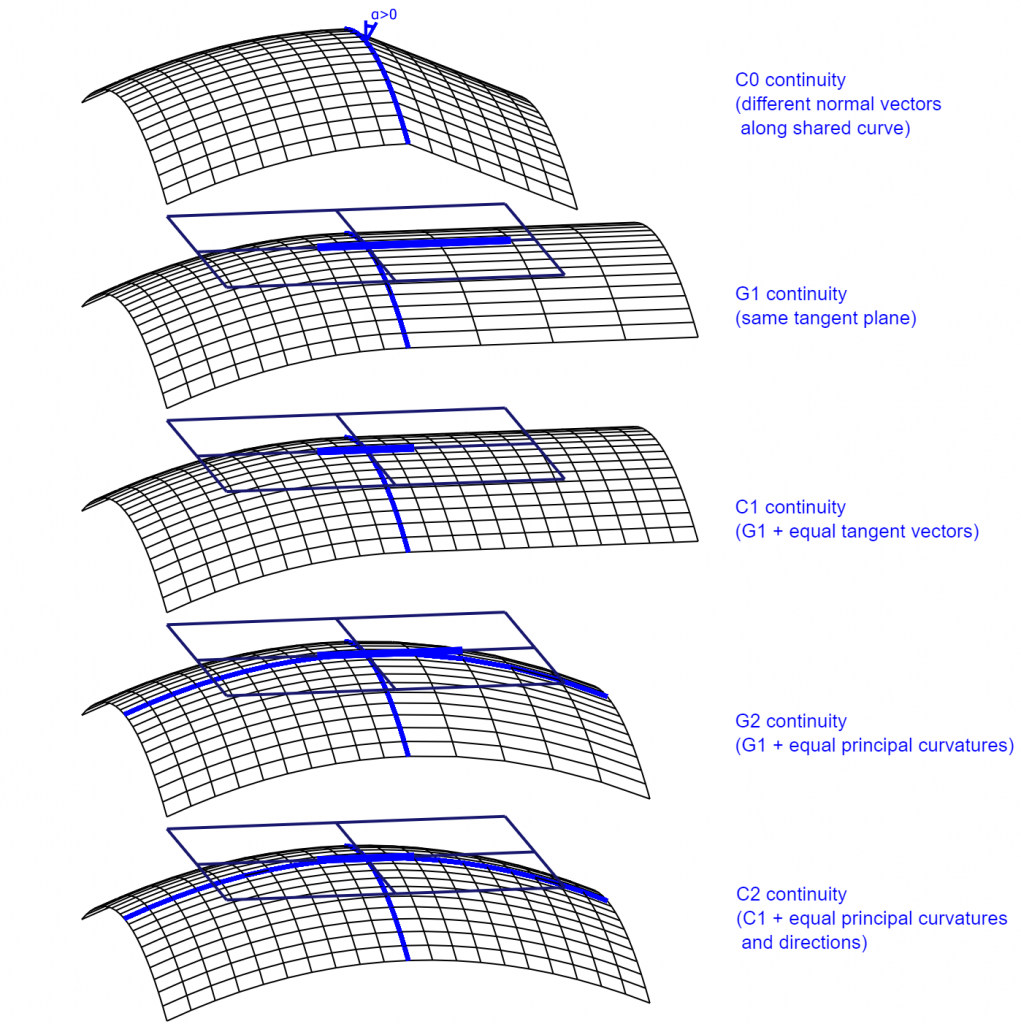
针对单个曲面，两个曲面的连接（参见上图）仅在每个交点定义其连续性。连接的平滑度是相交曲线上连续性的最小值。

共享边的规律性

边缘的规则性是共享该边缘的两个面连接的平滑度。换句话说，规律性是边上每个点的连接面之间的最小连续性。

边缘的规律性可以通过BRep_Builder::Continuity方法设置。要获得规律性，请使用BRep_Tool::Continuity方法。

一些算法，如Fillet，通过自己的算法设置生成边缘的规律性。另一方面，其他一些算法（如布尔运算、形状修复等）不设置规律性。如果需要在形状上正确设置规则，可以使用方法BRepLib::EncodeRegularity 。它为形状的所有边缘计算并设置正确的值。

规则标志被以下高级算法广泛使用：倒角，拔模角度，隐藏线去除，胶合。

形状的全局属性

形状的全局属性组件提供了用于计算 3D 空间中复合几何系统的全局属性的算法，以及查询计算结果的框架。

为系统计算的全局属性是：

• 大量的，
• 质心，
• 惯性矩阵，
• 绕轴的时刻，
• 绕轴的回转半径，
• 惯性的主要属性，例如主轴、主力矩和主回转半径。

几何系统通常被定义为形状。根据分析它们的方式，这些形状将提供以下属性：

• 从形状边缘引出的线条，
• 从形状的面诱导的表面，或
• 由形状包围的固体引起的体积。

可以将几个系统的全局属性组合在一起，得到由所有单个系统的总和组成的系统的全局属性。

形状的全局属性组件由以下部分组成：

• 用于计算形状全局属性的七个函数：一个函数用于线，两个函数用于曲面，四个函数用于体积。函数的选择取决于输入参数和用于计算的算法（BRepGProp全局函数），
• 用于计算一组点的全局属性的框架（GProp_PGProps），
• 一个通用框架，将多个基本框架保留的全局属性汇集在一起​​，并提供通用编程接口来查询计算的全局属性。

包GeomLProp和Geom2dLProp提供计算曲线和曲面局部属性的算法

曲线（对于一个参数）具有以下局部属性：

• 观点
• 衍生物
• 相切
• 普通的
• 曲率
• 曲率中心。

曲面（对于两个参数 U 和 V）具有以下局部属性：

• 观点
• U 和 V 的导数）
• 切线（用于 U 和 V）
• 普通的
• 最大曲率
• 最小曲率
• 主要曲率方向
• 平均曲率
• 高斯曲率

可以使用以下方法：

• CLProps – 计算曲线的局部属性（切线、曲率、法线）；
• CurAndInf2d – 计算最大和最小曲率以及 2d 曲线的拐点；
• SLProps – 计算表面的局部属性（切线、法线和曲率）。
• 连续性——计算两条曲线交界处的规律性。

请注意，接受 B 样条曲线和曲面，但不会将它们切割成所需连续性的片段。这是全局的连续性，这是可见的。

曲线和曲面适配器

一些开放级联技术的通用算法理论上可能适用于多种类型的曲线或曲面。

为此，他们只需通过接口获取分析曲线或曲面所需的服务，以便使用单个 API，无论曲线或曲面类型如何。这些接口称为适配器。

例如，Adaptor3d_Curve是一个抽象类，它通过使用任何 3d 曲线的算法提供所需的服务。

GeomAdaptor包提供接口：

• 在几何曲线上；
• 在几何曲面上的曲线上；
• 在几何表面上；

Geom2dAdaptor包提供接口：

• 在Geom2d曲线上。

BRepAdaptor包提供接口：

• 在面上
• 在边缘

当您编写对几何对象进行操作的算法时，请使用Adaptor3d（或Adaptor2d）对象。

因此，如果您为该对象提供从Adaptor3d或Adaptor2d派生的接口，则可以将该算法用于任何类型的对象。这些接口易于使用：只需从Geom2d曲线创建一个适应曲线或曲面，然后将此适应曲线用作算法的参数？这需要它。

边界框

边界框用于许多 OCCT 算法。最常见的用途是作为过滤器，避免检查形状对之间的过度干扰（边界框之间的干扰检查比形状之间的干扰要简单得多，如果它们不干扰，则搜索相应形状之间的干扰没有意义）。一般来说，边界框可以分为两种主要类型：

• 轴对齐边界框（AABB）是边缘平行于世界坐标系（WCS）轴的框；
• 定向 BndBox (OBB) 在其自己的坐标系中定义，可以相对于 WCS 旋转。事实上，AABB 是 OBB 的一个特例。

下图说明了使用 OBB 优于 AABB 时的示例。

这张照片中的 AABB 受到干扰。因此，许多 OCCT 算法会花费大量时间来干扰形状。但是，如果我们检查未受到干扰的 OBB，则无需搜索形状之间的干扰。那时，OBB 的创建和分析比 AABB 的类比操作花费的时间要多得多。

在本节的后面部分，具有最小表面积的边界框将被称为最佳边界框。

在 OCCT 中，边界框是在Bnd包中定义的。Bnd_Box类定义 AABB，Bnd_OBB类定义 OBB。这些类包含以下常用方法（此列表不完整；有关详细信息，请参阅有关相应类的文档）：

• IsVoid方法指示边界框是否为空（未初始化）。
• SetVoid方法清除现有的边界框。
• Enlarge(…)扩展当前边界框。
• Add(…)根据需要扩展边界框以包含作为参数传递的对象（点、形状等）。
• IsOut(…)检查参数是否在当前 BndBox 的内部/外部。

BRepBndLib类包含从形状创建边界框（AABB 和 OBB）的方法。

一些使用 OBB 的算法的简要描述

从点集创建 OBB

该算法在 Thomas Larsson 和 Linus Källberg (FastOBBs.pdf) 的“Fast Computation of Tight Fitting Oriented Bounding Boxes”中进行了描述。它包括以下步骤：

1.选择ñ一个(ñ一个≥3)初始轴。
2.将每个给定点投影到每个选择的（在第 1 项中）轴。此时，选择每个轴的“最小”和“最大”点（即具有投影到该轴的最小和最大参数（相应地）的点）。IE2∗ñ一个积分将被保留，并且该集合可以包含相等的积分。稍后（除非另有说明）在此算法中，我们将使用这些2∗ñ一个点而已。
3.在每个轴的所有“最小”和“最大”点对中选择一对点（从第 1 项开始），最远的两个点。让p0和p1是这对的“最小”和“最大”点。
4.创建轴 e0{p0p1−→−} （即有方向p0p1−→−）。
5.选择点p2（来自第 2 项中定义的集合），它与沿着指向的无限线的最大距离和0轴。

进一步，让我们考虑三角形T0⟨p0,p1,p2⟩（即有vertices p0,p1 and p2)。即：

6.创建新轴：和1{p1p2−→−}, 和2{p2p0−→−},n {和0→×和1→},米0{和0→×n→},米1{和1→×n→},米2{和2→×n→}.
7.根据以下轴创建 OBB：{和0⋮米0⋮n},{和1⋮米1⋮n}和{和2⋮米2⋮n}. 选择最优的 OBB。
8.选择点q0和q1（来自第 2 项中定义的集合），它们与三角形平面的距离最大吨0（从这架飞机的两侧）。那时，q0沿轴具有最小坐标n, q1有一个最大坐标。
9.对三角形重复步骤 6…7吨1⟨p0,p1,q0⟩,吨2⟨p1,p2,q0⟩,吨3⟨p0,p2,q0⟩,吨4⟨p0,p1,q1⟩,吨5⟨p1,p2,q1⟩,吨6⟨p0,p2,q1⟩.
10.计算 OBB 的中心和它的一半尺寸。
11.使用中心、轴和半尺寸创建 OBB。

原文如下：

从点集创建最优 OBB

为了从一组点创建最佳 OBB，使用与上述相同的算法，但在逻辑上有所简化并增加了计算时间。对于最佳 OBB，有必要检查可以由极值点创建的所有可能轴。并且由于极值点仅对初始轴有效，因此有必要在每个轴上投影整个点集。这种方法通常提供更严格的 OBB，但性能较低。该算法的复杂性仍然是线性的，并且对于点集使用BVH，它是 O(N + C*log(N))。

以下是使用 125K 节点集的模型的最优和非最优 OBB 示例：

DiTo-14 不是最佳的 OBB

DiTo-14 的最佳 OBB

PCA 不是最佳的 OBB

在这种情况下，非最优 OBB 的计算耗时 0.007 秒，最优 – 0.1 秒，大约慢了 14 倍。这样的性能与通过 PCA 方法（见下文）创建此形状的 OBB 相当，这需要大约 0.17 秒。

最优 OBB 的计算由与PCA 算法相同的BRepBndLib::AddOBB方法中的IsOptimal标志控制。

这些算法在Bnd_OBB::ReBuild(…)方法中实现。

基于惯性轴创建 OBB

该算法包含以下步骤：

1. 计算三个惯性轴，这将是 OBB 的轴。
2. 根据第 1 项中的轴将源对象 *( TopoDS_Shape )* 转换为局部坐标系。
3. 为第 2 项中获得的形状创建一个 AABB。
4. 计算 AABB 的中心及其半维。
5. 将中心转换为 WCS。
6. 使用中心、轴和半尺寸创建 OBB。

一个点的方法 IsOut

1. 将点投影到每个轴。
2. 检查投影参数的绝对值是否大于对应的半维。在这种情况下，IsOut方法将返回 TRUE。

另一个 OBB 的方法 IsOut

根据“有向边界框的分离轴定理”，需要检查 15 个分离轴：盒子的 6 个轴和 9 个是它们的叉积。
解析轴的算法l如下：

1. 根据公式计算“长度”：大号j=∑2我= 0H一世⋅∣∣∣一个一世→⋅l→∣∣∣. 这里，一个一世是第j个BndBox（j=1…2）的第i个轴（X轴，Y轴，Z轴）。H一世是沿第 i 个轴的半维。
2. 如果∣∣∣C1C2−→−−⋅l→∣∣∣>大号1+大号2（在哪里Cj是第 j 个 OBB 的中心），则所考虑的 OBB 在轴方面不受干扰l.

如果 OBB 在至少一个轴（共 15 个）方面没有受到干扰，那么它们根本不会受到干扰。

原文如下：

方法为点或其他边界框添加

根据源点和给定边界框的所有顶点创建一个新的 OBB（请参阅从点集创建 OBB部分）。

添加形状

方法BRepBndLib::AddOBB(…)允许从复杂对象 *( TopoDS_Shape )*创建边界框。此方法使用从点集创建 OBB部分和基于惯性轴创建 OBB部分中描述的两种算法。

如果形状的外壳可以由其中包含的一组点表示，则使用第一种算法。即，只有以下元素是点集的来源：

• 三角剖分节点；
• Poly_Polygon3D的节点；
• 具有线性 3D 曲线的边的顶点位于平面中；
• 如果源形状不包含更复杂的拓扑结构（例如，源形状是边的组合），则边的顶点具有线性 3D 曲线；
• 如果源形状不包含更复杂的拓扑结构（例如，源形状是顶点的组合），则为顶点。

如果无法提取所需的点集，则使用基于惯性轴创建 OBB部分的算法来创建OBB。

包BRepBndLib包含用于创建形状 AABB 的方法BRepBndLib::Add(…)、BRepBndLib::AddClose(…)和BRepBndLib::AddOptimal(…) 。有关详细信息，请参阅参考手册。

OBB 创建算法的局限性

1. 从点集创建 OBB一节中描述的算法比基于惯性轴创建 OBB一节中的算法工作得更好（发现表面积较小的 OBB）和更快。然而，（通常）两种算法返回的结果并不总是最优的（即有时存在另一个具有较小表面积的 OBB）。此外，第一种方法不允许计算具有复杂几何形状的 OBB。
2. 目前，OBB 创建算法仅针对 3D 空间中的对象实现。