深入理解数值计算网格(3)–非结构化网格生成算法

通常说的非结构网格主要指非四边形和六面体网格，包含三角形，四面体，楔形，金字塔等， 在实际应用中最常用的还是三角形和四面体。本文也主要介绍三角形和四面体的生成算法。

 

非结构化网格自动生成主要包含三种方法：

1.Delaunay method

（关于此方法的汉语翻译特别杂，不建议用中文翻译）

2.Advancing-Front method（波前法）

3.Spatial decomposition based method

（基于空间分解方法）

 

1.Delaunay method

生成三角形最常用的方法是Delaunay方法，也是所有网格生成算法中的最“基础方法”，在很多开源软件中都有其方法的实现。

Delaunay三角网格定义：平面上的点集P是一种三角剖分，使得P中没有点严格处于剖分后中任意一个三角形外接圆的内部。简单讲，给出一堆离散点，Delaunay网格是满足所有网格质量最好的网格。

Delaunay方法目前有很多改进方法，只介绍其中最基础的一种方法:逐点插入法

 

生成算法：

1.给出一堆离散点，初始化三角形链表

2.给出一个大三角形包含所有离散点

3.计算三角形链表中的每一个三角形的外接圆圆心和半径

4.如果点在已知三角形外接圆内，则把三角形的三条边加入到边数组中，在三角形链表中删除该三角形

5.删除所有重复的边，重复步骤3

6.用点和边数组中的每条边都组合成一个三角形，加入到三角形链表中，重复步骤2

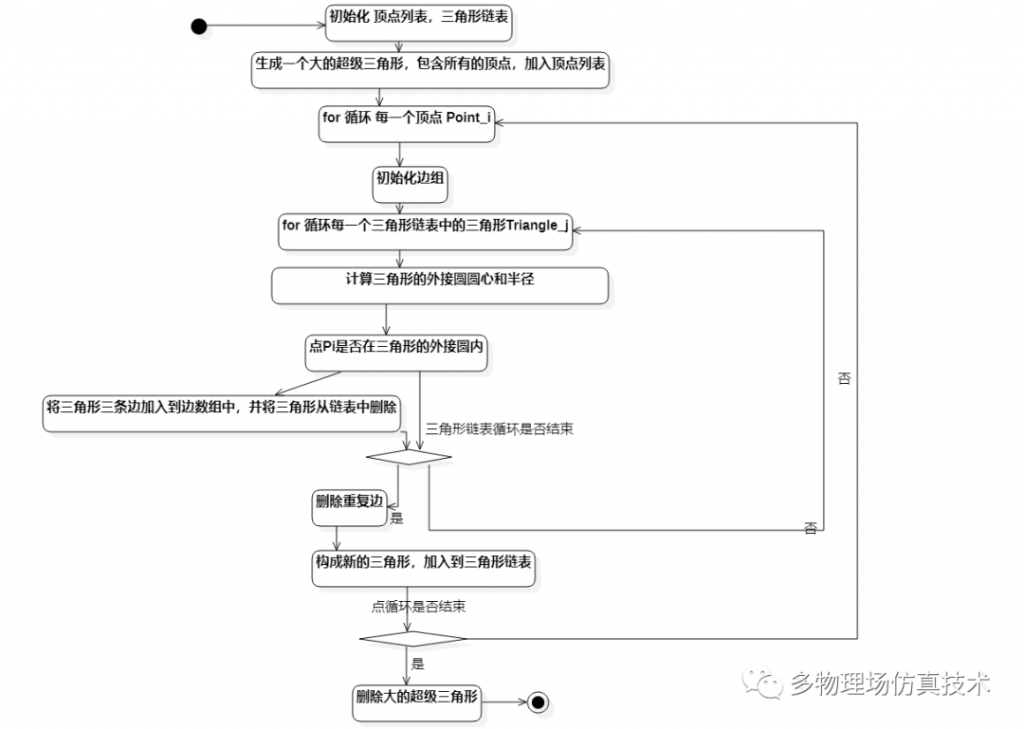
 Delaunay网格插入点UML活动图

 

作为基础的网格生成算法，Delaunay不仅支持二维，而且也支持三维。在三维计算中，只需将外接圆的判断改为外接球的判断即可。

 

2.Advancing-Front method（波前法）

Advancing-Front 方法又叫波前法，前沿推进法等。

其核心思想是沿着原始的网格边界生成网格，然后逐步推进生成，类似于波浪向未划分网格区域前进，直到所有区域被网格填满。

波前法思路清晰，尤其适用于已知边界的情况，其网格属性在生成过程中可以动态调整，控制性好，最终生成的网格质量也比较好，是生成非结构化网格的基础算法之一，同时Advancing-Front 方法的经过改进，也适用于四边形和六面体等结构化网格生成。

 

经典的波前法对二维从一组边开始，对三维从一组三角形面开始。以二维为例，网格生成策略一方面逐个单元逐个单元生成，创建插入新点和新单元，同时新的单元和之前的单元保持连通性。算法的一个关键点是如何插入新的点，新的单元需要满足网格尺寸和单元质量要求，波前法的一个优势是启发式（heuristic）算法，可以生成高质量，梯度可控的网格。相比其它算法，边界的完整性可以得到保证。其不足是在三维方法时，有可能出现不收敛的情况，即有些区域很难完全填充网格。

 

波前法的典型流程：

1. 定义网格输入数据和参数，包括整几何区域，边界，网格尺寸，网格梯度

2. 离散边界

3. 从边界任意位置开始，逐步插入点，形成单元，迭代指导求解区域被网格填满

 

在这个过程中，如何插入点和形成单元是算法最核心的部分，其涉及到：

1. 前进方向的单元选择

2. 前进分析以及定义最优点需要考虑的各种可能性

3. 单元构建有效性分析

4. 选择合适的数据结构

 

相比较其它方法，波前法在三维实现上要远远高于二维。三维需要考虑更多的因素和特殊情况，同时在算法效率上，三维的要求也更高。

 

3.Spatial decomposition based method

（基于空间分解方法）

基于空间分解方法相对简单，主要用到空间树结构，即二维四叉树和三维八叉树。以平面四叉树为例：

1. 根据几何对象，创建合适的树边界

2. 根据对象点的分布，创建四叉树结构

3. 在每个四叉树内部，利用四叉树的边和点，生成网格

4. 调整网格，使其满足网格质量要求和梯度分布

    

 

一个典型的例子如下：

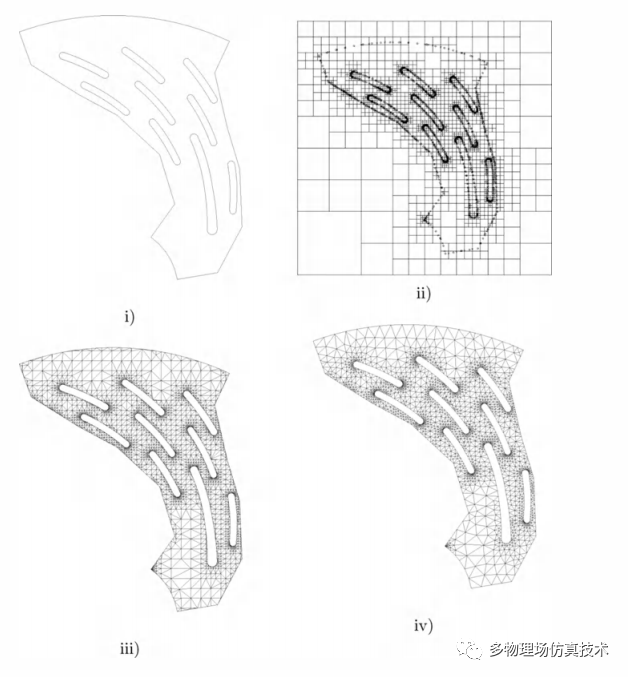
对于使用四叉树和八叉树方法生成网格，两个核心点：

1. 动态生成不平衡的树，即每个同级的树结点数目并不相同；

2. 在树结点内部选择合适的算法生成初始网格

 

笔者在几何，图形，网格，求解器开发中，都较多的使用到了八叉树结构，八叉树结构可以说是一种基础性的数据结构和方法。

 

三种方法生成的网格比较：

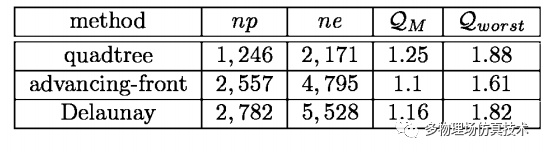
np为点的数目，ne为单元的数目，Qm为网格的质量，Qworst为最差的网格质量

 

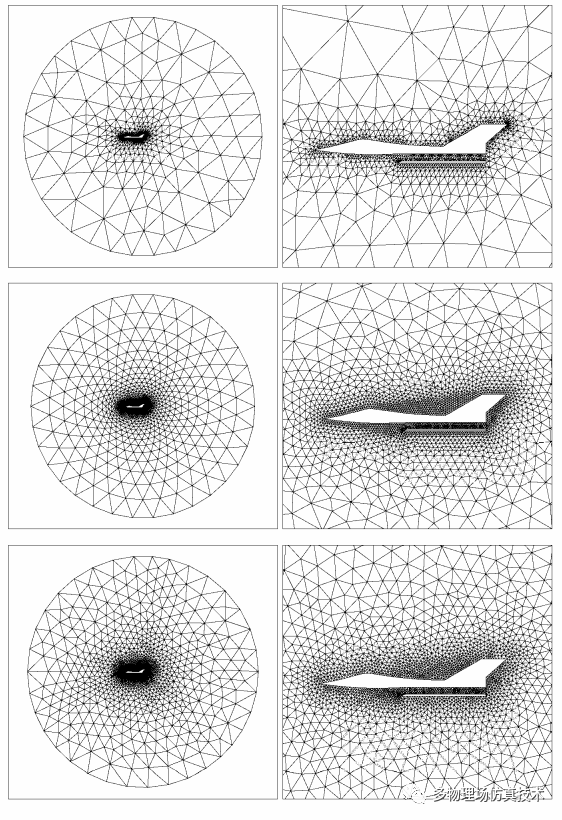
图片从上往下方法分别是：

四叉树,波前法,Delaunay     

图片皆来自于书 Mesh Generation (Application to Finite Elements)，考虑到网格参数设置的差异，重点关注网格质量和分布

 

在实际应用中，三种方法并不是独立存在，经常会有方法混用的情况，比如在CFD网格中，不同区域采用不同的网格策略，可能效率和稳定性更好。

 

本文介绍了非结构化网格的三种常用方法，其中树结构方法和delaunay方法是比较常用的方法，作为研发人员，应该熟练掌握，最好能独立开发相关算法。

 

参考书目：

Mesh generation Application to Finite Elements

Finite element mesh generation