工业机器人（4）– Matlab Robot Toolbox运动学正、逆解-卡核

【Matlab Robotics Toolbox】robotics toolbox学习及使用记录，方便自己后面复习、改进。
基于Matlab R2019b 9.5; Peter Corke的Robotics Toolbox 10.3.1

0. 前言

Robot toolbox- rtbdemo

0. 前言

在初学机器人学的时候，面对大量的概念和复杂的公式，往往不知道从何开始入手。一味的啃机器人学的概念和公式枯燥又无味，坚持不了几天就从入门到放弃一条龙走完了。坚持下去的动力之一就是能尽快看到自己的学习成果，而MATLAB机器人工具箱就是非常简单的机器人平台快速搭建工具。

本文主要介绍如何使用matlab工具箱建立机器人模型，并对其进行绘制。这里使用的RTB工具箱10.3版本，不同版本间代码风格可能会有差异，因此请注意工具箱的使用版本。

Robot toolbox- rtbdemo

rtbdemo是工具箱自带的一个历程脚本，在命令行窗口输入：

rtbdemo

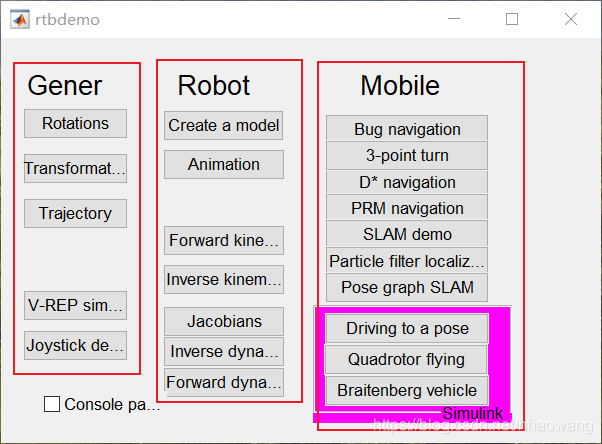
RTB GUI界面：
图片[1]-工业机器人（4）– Matlab Robot Toolbox运动学正、逆解-卡核
如字面意思，左边一列是通用函数的例子（如：旋转，平移，轨迹等）；中间主要是机械臂的基础函数，右边为移动机器人的一些历程。这些功能都写的很清楚了，都可以随便点点看，会很有意思。
本博客主要专注于机械臂的搭建和使用，因此会对前两列的函数进行展开介绍。

1. 依据D-H参数建立机器人模型

标准D-H参数示意图

以经典的4轴机械臂Scara为例（因为既有转动关节又有移动关节），介绍一下机械臂建立的步骤，首先上代码：

clear ; clc; close all;
% 机器人各连杆DH参数
% Scara机械臂连杆偏距参数d
d1 = 200;
d2 = 86;
d3 = -92;
% 由于关节4为移动关节，故d4为变量，theta4为常量
theta4 = 0;

% Scara机械臂连杆长度参数a
a1 = 400;
a2 = 250;
a3 = 0;
a4 = 0;

% Scara机械臂关节偏角参数alpha
alpha1 = 0 / 180 * pi;
alpha2 = 0 / 180 * pi;
alpha3 = 180 / 180 * pi;
alpha4 = 0 / 180 * pi;
% 定义各个连杆以及关节类型，默认为转动关节
%           theta      d        a        alpha 
L(1)=Link([  0         d1      a1      alpha1]); L(1).qlim=[-pi,pi];
L(2)=Link([  0         d2      a2      alpha2]); L(2).qlim=[-pi,pi]; L(2).offset=pi/2;
L(3)=Link([  0         d3      a3      alpha3]); L(3).qlim=[-pi,pi];
% 移动关节需要特别指定关节类型--jointtype
L(4)=Link([theta4       0      a4      alpha4]); L(4).qlim=[0,180]; L(4).jointtype='P';
% 把上述连杆“串起来”
Scara=SerialLink(L,'name','Scara');
Scara.display(); % 显示Scara机器人关节数以及D_H参数列表
% Scara:: 4 axis, RRRP, stdDH, slowRNE    

% 定义机器人基坐标和工具坐标的变换
Scara.base = transl(0 ,0 ,305);
Scara.tool = transl(0 ,0 ,100);
Scara.teach();   


% 运动学正解
pose_0=[pi/4,-pi/3,pi/2,100];
T=Scara.fkine(pose_0);
cchain=Scara.trchain;

% 运动学逆解
% 当反解的机器人对象的自由度少于6时，要用mask vector进行忽略某个关节自由度%
mask_vector = [1,1,1,0,0,1];
axi_val = Scara.ikine(T,'mask',mask_vector,'pinv');
% We can help the solution along by using the 'pinv' option

% 雅可比矩阵
% j0=robot.jacob0(pose_0);

命令行显示Scara机器人信息和D-H参数表：

GUI显示机器人模型

2. 代码解释

单个Link的解释

%           theta      d        a        alpha 
L(1)=Link([  0         d1      a1      alpha1]); L(1).qlim=[-pi,pi];
L(2)=Link([  0         d2      a2      alpha2]); L(2).qlim=[-pi,pi]; L(2).offset=pi/2;
L(3)=Link([  0         d3      a3      alpha3]); L(3).qlim=[-pi,pi];
% 移动关节需要特别指定关节类型--jointtype
L(4)=Link([theta4       0      a4      alpha4]); L(4).qlim=[0,180]; L(4).jointtype='P';

Link函数是根据DH参数建立连杆，其中包含了关节的信息，DH的输入顺序见代码；
qlim指定关节极限，注意，工具箱中的移动关节变量不允许有负值；
jointtype指定关节类型，默认为转动关节，L(4).jointtype='P’意味着第四根link是由移动关节连接的；
offset为关节初始值的偏置。这里要注意的是，定义好关节类型后，相应的变量必须为0，初值必须由offset定义，例如，关节2为转动关节，那么L(2)的theta必须为0，但是我们又希望初始状态下关节2能有一个偏置，那么就通过 L(2).offset=pi/2;来实现。
另外这里还有一个常用的基于改进的DH建立模型的方法，程序中没有说明，格式为：

L(1)=Link([0 d1 a1 alpha1], 'modified');

建立机器人整体的解释

Scara=SerialLink(L,'name','Scara');

L为刚刚建立好的四根link，‘name’为可选项，可以不加，就是给机器人取个名字，看它骨骼惊奇，这里就叫它‘Scara’啦。
同样的，SerialLink函数还有其他的可选则项在此不一一介绍，欲了解则：

help SerialLink

这条语句就建立了一个叫Scara的机器人类型的对象，下面就可以对他操作了。

% 定义机器人基坐标和工具坐标的变换
Scara.base = transl(0 ,0 ,305);
Scara.tool = transl(0 ,0 ,100);

具体含义为，把我们的Scara基部沿着z轴平移305mm，工具坐标系则以最后一个坐标为基础，沿z方向平移100mm.
transl函数涉及到工具箱中对旋转、平移以及齐次坐标的变换，可参考Matlab机器人工具箱（0）——旋转与平移变换

Scara.teach();

字面意思，对机器人进行示教。

运动学正解


% 运动学正解
pose_0=[pi/4,-pi/3,pi/2,100];
T=Scara.fkine(pose_0);
cchain=Scara.trchain;

绘图


joint(: , 1) = linspace(-pi/8,pi,200);
joint(: , 2) = linspace(-pi,pi/4,200);
joint(: , 3) = linspace(pi/3,-pi/2,200);
joint(: , 4) = linspace(0,360,200);
Scara.plot(joint ,'jointdiam',1,'fps',100,'trail','r-')

运动学逆解


% 运动学逆解
% 当反解的机器人对象的自由度少于6时，要用mask vector进行忽略某个关节自由度%
mask_vector = [1,1,1,0,0,1];
axi_val = Scara.ikine(T,'mask',mask_vector,'pinv');
% We can help the solution along by using the 'pinv' option

T为我们刚刚正解得到的齐次变换矩阵，输出为关节向量。
常用可选项：
‘mask’,M: mask vector (6×1) that correspond to translation in X, Y and Z, and rotation about X, Y and Z respectively.这里Scara机器人只有四个自由度，在x，y两个方向的旋转不存在自由度，因此为[1 1 1 0 0 1]；
’q0’,Q为求解提供一个关节初值，因为数值法逆解可能不会收敛到想要的构型，提供一个初值，可以增大得到我们想要构型的概率。
’lambda’,L ： initial value of lambda (default 0.1) 数值解法的步长，如果求解失败，可以减小步长再尝试，当然减小步长意味着求解时间更长；
’tol’,T容许误差，精度要求不高的话可以适当调大一点，默认为1e^-10
’ilimit’,L迭代的最大次数，求解失败时可以适当增大重新尝试。
’transpose’,A迭代时使用雅克比的转置代替伪逆，关于这两种方法的异同和思想，可参考https://www.ilovematlab.cn/thread-533863-1-1.html?s_tid=LandingPageTabqa
其他可选项有需求可参考

微分运动学（求雅克比矩阵）

Scara.jacob0(joint)

继续傻瓜操作。
输入关节角，输出6xN的雅克比矩阵，N为机械臂的自由度数，这里N为4。
有时候需要求雅克比矩阵的逆或伪逆，顺便一提matlab矩阵求逆和伪逆的函数：

% 矩阵求逆，mat为待求解的矩阵
inv(mat)
% 矩阵求伪逆
pinv(mat)

参考

https://blog.csdn.net/weixin_43502392/article/details/105447785

https://blog.csdn.net/weixin_45629652/article/details/103831764

文章版权归作者所有，未经允许请勿转载。

THE END

综合
# 工业机器人