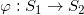清华笔记：计算共形几何讲义 （4）单纯同调

 

这次课程，我们介绍单纯同调理论。在代数拓扑中，有单纯同调、奇异同调和de Rham同调理论。它们所用的数学工具不同，但是理论彼此等价。【1】给出了本课程的视频链接。

 

基本方法

代数拓扑的目的是将拓扑范畴的问题转换成代数范畴的问题，用代数方法加以解决。最为基本的问题之一就是判断两个拓扑空间是否同胚。在理想情形下，我们为每一个空间配上一系列群结构，如果这些群彼此同构，则空间拓扑同胚。但是，目前代数拓扑的方法还没有到达这一程度。同调群同构只能推出空间伦型等价。伦型等价远远弱于拓扑等价。

 

同调论的基本方法是将流形三角剖分，然后将子流形表示成单形的线性组合，所有的子流形构成线性空间。将拓扑算子（边缘算子）表示成线性算子（矩阵），用线性代数的方法来获取拓扑信息。

 

同调方法将低秩、稀疏，高度非线性的拓扑性质变换成高维空间的线性运算，非常具有启发意义。

拓扑去噪应用

图1. 曲面上的环柄圈（绿色 handle loop）、隧道圈（红色 tunnel loop）。

 

如图1所示，给定一个嵌在三维欧氏空间中的高亏格曲面，曲面将三维欧氏空间分为内部和外部，存在一族同伦群的基底，, 这里亏格。直观上，其中有条圈在内部可以缩成点，但在外部中无法缩成点，它们构成外部空间的同伦群的基底，被称为是隧道圈（tunnel loop）；另外条圈在外部中可以缩成点，但在内部中无法缩成点，它们构成内部的同伦群的基底，被称为是环柄圈（handle loop）。环柄圈和隧道圈对于医学图像具有重要意义。

图2. 医学图像中的拓扑去噪。

 

如图2所示，我们用CT断层扫描技术获取直肠切面图像，经过曲面复建得到直肠曲面。由于图像分割的误差，复建的曲面有很多虚假的亏格（环柄）。在实际应用中，我们需要检测这些虚假亏格。这些环柄非常微小，用肉眼无法直接检测。唯一的方法就是通过计算拓扑方法得到，这往往依赖于曲面的环柄圈和隧道圈的算法。

单纯同调理论

 

相对于曲面而言，同伦群和同调群保留了相同的信息，因此彼此等价；对于三流形而言，同伦群反映的信息远远多于同调群，同伦群强于同调群。但是，同伦群本身为非阿贝尔群（非交换群），判定两个非阿贝尔群是否同构是非常繁难的问题。相反，同调群是同伦群的阿贝尔化，阿贝尔群的计算只需要线性代数。

图0.同伦群是非阿贝尔群。

 

如图所示，环路无法在曲面上缩成一个点，因此同伦群中，同时，我们得到。因此亏格为2的曲面的同伦群不可交换。

 

我们记的中心交换子群为所有形如生成的正规子群，

那么商群

为一阿贝群，即为曲面的一维下同调群。换句话说，同调群是同伦群的阿贝尔化。

 

环路在同伦群中不是单位元，但是在同调群中却是单位元。几何上来看，将曲面分成两个连通分支，是其中一个分支的边缘。这意味着，在同调群中，边缘环路被视为单位元。

 

同调群概念的要义在于：边的边为空，圈和边的差别就是同调。

 

同调群的概念

 

单纯复形是曲面三角剖分的直接推广，但是单纯复形可以表示更为广泛的拓扑空间，例如非流形的空间。

 

单纯形 给定中一般位置的个点，维单纯形是这些点构成的凸包(convex hull)，

我们称为单纯形的顶点。如果另外一个单纯形包含在中，，我们称是的一个面。

 

单纯形是有定向的，每一个单纯形有两个定向，单纯形的定向由其顶点的排列给出。我们考虑数列的所有排列，它们构成对称群，其中所有由偶次对换（即只交换两个数的位置）构成的子群记为。如果排列属于，则单纯形的定向为正，反之定向为负。

 

通常意义下的点，线段，三角形，四面体就是0到3维的单纯形。

 

单纯复形 单纯形粘贴在一起就构成单纯复形。所谓一个单纯复形就是一组单纯形的并集，满足两个条件，

1.  如果一个单纯形属于，那么的所有面都属于，

2.  如果两个单纯形都属于，，那么或者它们的交集为空，或者它们的交集是它们共同的一个面。

 

通常意义下，曲面的三角剖分就是单纯复形。

图1. 复形上的1维和2维链。

 

链群 给定一个单纯复形，一个维链就是所维单纯形的线性组合，如图1所示，

,

所有的维链在加法下成一阿贝尔群（可交换群），记为,

.

其中零元为，的逆元为.

 

图2. 边缘算子。

 

边缘算子 维边缘算子是链群之间的一个同态

,

作用在单纯形上

,

作用在链上

。

直观上，边缘算子就是剥离每个链的边界。

 

通过直接计算，我们可得到

，

亦即边的边为空。

 

图3. 闭链和开链。

 

同调群 维链被称为是闭链，如果。所有的维闭链构成的一个子群，记为；如果存在一个维链，满足，那么被称为是恰当链，所有维恰当链构成一个子群，记为。因为边的边为空，所以恰当链必为闭链，

。

给定单纯复形，我们得到链复形，

具有条件。

 

图4. 恰当闭链和非恰当闭链。

 

综上所述，边（恰当链）一定是圈（闭链），圈可能不是边。圈和边的差别就是同调

 

，

如图4所示，左帧显示了恰当的闭链，每一个闭链都包围着一个曲面区域，因此是边缘。右帧是非恰当的闭链，这条链并不包围任何一个曲面区域。如果我们把曲面沿着切开，我们得到一个圆筒面，圆筒面有两个边缘曲线，

，

但是本身并不构成圆筒面的边界。

 

我们将单纯复形的所有同调群放在一起，记为。

 

同调群的计算

 

曲面一维同调群的基底和曲面基本群基底相同，我们可以用基本群的组合算法来计算一维同调群基底。高维同调群的算法基于线性代数的矩阵特征值和特征向量算法。

 

我们可以将链群视为线性空间，边缘算子是线性算子，因此可以被表示为矩阵。假设复形所有的维单纯形为

，

它们线性张成维链群

；

复形所有的维单纯形为

它们线性张成维链群

。边缘算子具有矩阵表示，

,

这里联接数是一个整数，定义如下：如果，则为0；如果是的一个边缘面，，则为+1；如果是的一个边缘面，，则为-1。

 

如此，我们构造离散拉普拉斯算子：

,

的基底是的对应于0特征根的特征向量。

 

这里，是整数矩阵，存在Smith 标准型（Smith Normal Form）：存在可逆整数矩阵和, 为对角阵，

这里, 整除，并且

是所有阶子矩阵行列式的最大公因子。

 

伦型不变量

 

单纯映射 假设是拓扑空间之间的连续映射，我们可以将M和N用单纯复形来逼近，同时映射本身可以用所谓的单纯映射来逼近。所谓单纯映射，就是说对于M中的任意一个单纯形，其像是N中的单纯形。给定一个连续映射，我们可以将M和N进一步细分(subdivision)，在细分后的复形上定义单纯映射来逼近连续映射。可以证明，对于任意给定的误差，我们可以将M和N细分的足够细腻，使得单纯映射和连续映射的误差小于给定的阈值。单纯映射可以表示成分片线性映射，图中，我们显示一个单纯映射的实例，从小女孩的雕像到单位球面的形变。现实生活中，所有的动漫动画都是基于单纯映射的理论。

 

链映射 C和D是M和N的链复形，

单纯映射诱导了链复形之间的映射，被称为是链映射,

同时对于每一维度，单纯映射和边缘算子可交换，

，

因为单纯映射将闭链映为闭链，链映射诱导了同调群间的同态，, 。

 

链同伦 假如映射彼此同伦，它们诱导的链映射, , 满足如下条件

这里T是一系列同态,满足

，

这两个链映射被称为是链同伦。

 

是同伦，并且，那么同伦F将M中的低维链映到N中的高一维链，诱导了同态T。如下图所示，是M上的一条路径，关系式成立：

 

图5. 链同伦的直观解释。

 

我们考察所诱导的同调群间的同态，令为一闭链，则，

,

因此和相差一个边缘链，彼此同调。因此彼此相等。如此，我们证明了同伦映射诱导相同的同调群同态。

 

伦型等价 假如存在连续映射和，满足，并且，就是说f和g的复合同伦于N上恒同映射，g和f的复合同伦于M上的恒同映射，则我们说拓扑空间M和N同伦等价，或M和N具有相同的伦型。如上讨论，我们得出同伦等价的空间具有同构的同调群。

 

形变收缩核 假如B是A的子空间，B是A的形变收缩核，是指B可以在保持A上各点不变的情况下连续形变到A上。这样形变收缩映射与自然包含构成了同伦等价关系。一个拓扑空间和其形变收缩核具有相同的同调群。

 

环柄圈和隧道圈算法

在【2】中，孙剑等给出了环柄圈和隧道圈的计算方法。这里，给定一个嵌在三维欧氏空间中的高亏格曲面，曲面将三维欧氏空间分为内部和外部，存在一族同调群的基底，, 这里亏格。直观上，其中有条圈在内部同调于0，但在外部非同调于0，它们构成外部空间的同调群的基底，被称为是隧道圈（tunnel loop）；另外条圈在外部中同调于0，但在内部中无法缩成点，它们构成内部的同伦群的基底，被称为是环柄圈（handle loop）。

 

计算环柄和隧道圈的核心想法有两个：过滤（filtration）和配对（pair）。一个单纯复形的过滤（filtration）是一系列嵌套的复形：

。

我们可以假设每一步，即添加一个单纯形。每一次我们添加一个维单纯形，有两种可能性：

 

1. 生成一个维非边界闭链，这时我们称为正的单形；

2.消灭掉一个维已经存在的闭链，这时我们称为负的单形。我们将被消灭掉的闭链中最后一个正单形和配对。

 

我们将曲面三角剖分，再取一个实心球，包含曲面。再对进行三角剖分，使得的三角剖分限制在上，等于的三角剖分。球外取一点，边界上的每个三角形都和连成一个四面体。如此，我们得到了一个三维球面的一个三角剖分，同时得到内部、外部和曲面的三角剖分。

 

我们首先构造曲面的一个过滤序列，然后逐步添加单形构造内部的过滤序列，最后在添加单形，构成整个的过滤序列。

1. 在完成曲面的过滤后，存在个没有被配对的正单形，对应着个同调群的基底。

2. 在完成内部的过滤后，会有上个正单形被配对，它们对应着个环柄圈。

3. 剩下的个正单形，对应着个隧道圈。

计算细节可以在【2】中找到。

 

 

---

References:

【1】http://www.iqiyi.com/w_19rtrpkd5x.html

【2】T.Dey, K. Li, J. Sun and D. Cohen-Steiner, "Computing Geometry-aware Handle and Tunnel Loops in 3D Models", SIGGRAPH 2008.

---

 

 

【老顾谈几何】邀请国内国际著名纯粹数学家，应用数学家，理论物理学家和计算机科学家，讲授现代拓扑和几何的理论，算法和应用。回复“目录”，可以浏览往期精华。

转载本文请联系原作者获取授权，同时请注明本文来自顾险峰科学网博客。
链接地址：https://blog.sciencenet.cn/blog-2472277-1173812.html

上一篇：清华笔记：计算共形几何讲义 （2）代数拓扑
下一篇：清华笔记：计算共形几何讲义 （6）上同调的霍奇理论