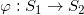清华笔记：计算共形几何讲义 （6）上同调的霍奇理论

这次课程，我们介绍霍奇分解定理，这一定理在图形学、视觉和网络中，应用非常广泛。直观而言，我们考察曲面上的切向量场，如果这个向量场光滑得无以复加，那么这个向量场被称为是调和场（harmonic field）。霍奇分解定理是说曲面上任意一个光滑切向量场，可以被唯一地分解为三个向量场：梯度场、散度场和调和场。霍奇分解经常被用于光滑化一个矢量场，将一个不可积矢量场变得可积。本次视频链接在【1】中可以找到。

图1. 曲面调和1-形式群的基底。

在几何应用中，很多时候我们需要在一类对象中选择一个代表元。在最为理想的情况下，代表元是唯一的。比如

从更高的观点来看，调和形式是流形上椭圆型偏微分方程的解，其解空间的维数（同调群的维数）由流形的拓扑所决定。这正是指标定理的精髓。指标定理联结了分析（偏微分方程）和拓扑（上同调群）。

曲面上所有无旋无散矢量场成群，此群和曲面的上同调群同构，这就是所谓的霍奇(Hodge)理论。

图2. 平面区域上的电场。

曲面上的无旋无散场（旋度为0，散度为0的场）的现实世界模型就是静电场，也可以理解为曲面上光滑得无法再光滑的矢量场。详细解释，请参考【2】。

那么，曲面上的静电场又该如何描述？

曲面静电场 调和场的概念可以推广到曲面上，如图3所示，红色轨道表示等势线，蓝色轨道表示电力线。曲面上的电场强度切矢量场为无旋无散的调和场。

图3. 亏格为二的曲面上的调和矢量场。

图4显示的是另外一个调和切矢量场，同样无旋无散。

图4. 亏格为二的曲面上的调和矢量场。

上式给出了调和场的椭圆型偏微分方程。

那么，自然的问题就是：调和形式存在吗？如果存在，解唯一吗？如果不唯一，那么所有的解空间的维数如何？所有解构成的群结构如何？Hodge理论给出了所有这些问题的解答：所有的调和k-形式构成群，调和k-形式群和流形的k阶上同调群同构。

图5. 女孩曲面上的调和1-形式。

Hodge理论本质是说：每一个上同调类中有且仅有一个调和微分形式。这个定理有两层意思，一是存在性，二是唯一性。

图6. 对偶剖分。

出于计算的目的，我们需要将经典光滑流形的霍奇理论离散化，假设光滑曲面被一个单纯复形所近似，单纯复形嵌入在三维欧氏空间之中，因而具有诱导的欧氏度量，我们称之为带度量的离散曲面。我们构造顶点的Voronoi图（Voronoi Diagram）， 记为。对任意顶点，其对应的Voronoi胞腔为：

，

图7. 每条边和其对偶的长度之比。

离散泊松方程为对称正定稀疏线性系统，我们用共轭梯度方法可以求解。

References:

【1】http://m.iqiyi.com/w_19rtoay4k9.html#vfrm=8-8-u-1

【2】苏变萍，陈东立，《复变函数与积分变换》，高等教育出版社。

原文发布在【老顾谈几何】公众号 （2017年7月12日）

转载本文请联系原作者获取授权，同时请注明本文来自顾险峰科学网博客。
链接地址：https://blog.sciencenet.cn/blog-2472277-1175407.html

上一篇：清华笔记：计算共形几何讲义 （4）单纯同调
下一篇：清华笔记：计算共形几何讲义 （7）矢量场设计