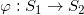清华笔记：计算共形几何讲义 （8）狭缝映射（Slit Map）的存在性

我们用较为初等的复变函数方法证明一种共形映射的存在性：狭缝映射（slit mapping）。如图所示，给定亏过为0的多连通曲面，存在共形映射将其映射到平面区域，每个边界的联通分支都被映成一条狭缝（slit）。这里所用的数学证明方法比较巧妙，令人赏心悦目。真正的计算和需要应用全纯微分的方法。这篇笔记和罗锋教授讨论过。

图1. 构造狭缝映射（slit map）。

后面我们会详细解释狭缝映射（Slit Map）的算法，主要的理论工具是全纯1-形式。

原文发布在【老顾谈几何】公众号 （2017年7月16日）

转载本文请联系原作者获取授权，同时请注明本文来自顾险峰科学网博客。
链接地址：https://blog.sciencenet.cn/blog-2472277-1177215.html

上一篇：清华笔记：计算共形几何讲义 （7）矢量场设计
下一篇：清华笔记：计算共形几何讲义 （8）狭缝映射（Slit Map）的存在性