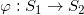清华笔记：计算共形几何讲义 （19）离散曲面曲率流 （Discrete Surface Ricci Flow ) I

【上课时间：每周二和周四上午9:50-11:20AM；地点：清华大学，近春园西楼三楼报告厅。欢迎任何有兴趣的朋友，前来旁听指导。】

图1. 曲面单值化定理：所有带度量的封闭曲面都可以保角地映到三种标准空间中的一种：球面，欧氏平面，双曲平面。

图2. 黎曼映照。

图3.离散曲面

图4. 常曲率三角形。

图5. 离散曲率。

图6. Derivative Cosine Law.

图7. Cotangent Edge Weight。

图8. 拓扑四边形。

图9. 拓扑圆筒的共形模。 

图10. 拓扑环带的共形模。

图11. 拓扑多孔环带的共形模。

图12. 拓扑轮胎的共形模。

图13. 亏格为1的曲面带有3个边界。

原文发布在【老顾谈几何】公众号 （2017年8月12日）

转载本文请联系原作者获取授权，同时请注明本文来自顾险峰科学网博客。
链接地址：https://blog.sciencenet.cn/blog-2472277-1201057.html

上一篇：清华笔记：计算共形几何讲义 （18）拟共形映射（Quasi-Conformal Map）
下一篇：清华笔记：计算共形几何讲义 （20）离散曲面曲率流 （Discrete Surface Ricci Flow）II