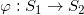清华笔记：计算共形几何讲义 （20）离散曲面曲率流 （Discrete Surface Ricci Flow）II

为了证明离散曲率流解的存在性，我们需要一些较为独特的数学工具，特别是双曲几何的理论知识。这次课程，我们讲解简单的双曲几何知识，特别是如何将一个带有锥奇异点的平直度量变换成完备双曲度量带有尖点，和Decorated双曲度量。然后，我们用双曲几何来解释离散熵能量。

图1. hyperbolic lines，Ideal hyperbolic triangles。

图2. Thurston's shear coordinates。

图3. Penner's decorated triangle.

图4. hyperbolic ideal tetrahedron。

图5. 长度交比 Cross ratio。

图7. 欧氏度量的顶点缩放操作。

图8. decorated 双曲度量的decoration缩放操作。

图9. 离散曲率流的双曲几何解释。

图10. 辅助函数的构造。

这次课程，我们讲解了离散曲率流熵能量的双曲几何解释，将平直度量和双曲度量建立了联系。后继课程，我们会证明解的存在性和收敛性。

单纯从计算机算法实现角度而言，这些理论知识并不直接需要。但是，如果我们为了证明这一算法解的存在性，双曲几何必不可少。从短期的发表工程论文角度而言，这些努力是得不偿失的；但是从长远的历史观点来看，为了理论的严密性，我们花费的心血是值得的。

Reference

• Alexander Bobenko, Discrete Conformal Maps and Ideal Hyperbolic Polyhedra, Geometry and Topology 19(2015), 2155-2215

• X. Gu, R. Guo, F. Luo, J. Sun and T. Wu, A discrete Uniformization theorem for polyhedral surfaces I, Journal of Differential Geometry, 2016 (arXiv:1309.4175)

• X. Gu, R. Guo, F. Luo, J. Sun and T. Wu, A discrete Uniformization theorem for polyhedral surfaces II, Journal of Differential Geometry, 2016

  (arXiv:1401.4594) 

原文发布在【老顾谈几何】公众号 （2017年8月13日）

转载本文请联系原作者获取授权，同时请注明本文来自顾险峰科学网博客。
链接地址：https://blog.sciencenet.cn/blog-2472277-1202473.html

上一篇：清华笔记：计算共形几何讲义 （19）离散曲面曲率流 （Discrete Surface Ricci Flow ) I
下一篇：清华笔记：计算共形几何讲义 （21）离散曲面曲率流 （Discrete Surface Ricci Flow）III