3、Assimp的导入标志

  一般的模型文件中，大多数情况下在建模时默认都保存成了OpenGL的右手坐标系，即z轴坐标垂直屏幕向外。而在D3D中习惯是左手坐标系，即z轴垂直屏幕向里。左右手坐标系区别如下图所示：

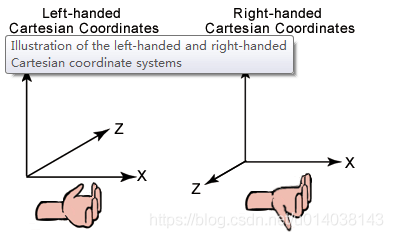
  其实这种差别，对于现代的可编程的渲染管线来说，无论是OpenGL还是D3D都是可以随意使用左右手坐标系的，无非就是使用列矩阵左乘向量还是用行矩阵右乘向量的差别。这最终就变成了开发人员的事情，即你是习惯左手还是右手？

  在本系列教程中，为了保持"D3D祖传的左手风格"，编译Shader时都加上了D3DCOMPILE_PACK_MATRIX_ROW_MAJOR标志，这样Shader中的矩阵都是行主序的，编写变换Sheder程序时，就是用矩阵挨个右乘向量即可，在阅读和理解矩阵变换顺序上就是从左到右的自然阅读顺序，至少我是比较喜欢这样的阅读顺序，跟平时看书的自然顺序是一致的。同时使用这个标志编译Shader后，在使用DirectXMath库生成的矩阵传入Shader时就不用麻烦的做矩阵转置操作了，因为DirectXMath库本身也是行主序操作矩阵的。这样本系列教程中Shader就“一路向西”了。

  Assimp在导入模型时，可以通过设置导入标志aiProcess_ConvertToLeftHanded的方式，强制模型数据转换为左手坐标系，当然这是通过Assimp的“后处理”方式来实现的，因此称这个标志为“导入后处理”标志更合适。需要注意的是这些“后处理”的标志并不会改变原始的模型文件的数据，只是对Assimp加载进内存的数据进行了变换，所以不用担心会损坏原始的模型文件。

  另外，很多模型文件，因为建模时美工设计的原因，所以还会有很多丰富的网格模式，对于OpenGL来说，这些基本不是大问题，但是对于用D3D12渲染来说可能会有问题，因为之前已经介绍过，D3D12在功能上比OpenGL上就弱一些，比如：D3D12最多仅支持到三角形网格渲染，但是OpenGL就支持n边形（n可以大于等于3）的数据渲染，这个差别其实并不重要，因为任何n边形都可以方便的变成三角形，仅是一个算法上的区别，所以按照“D3D12向下”的风格，就不会过多的提供这样的支持。索性的是这些差异，都可以通过Assimp的“导入后处理”标志加以消除，在本章示例中，主要使用了如下的标志：

#define ASSIMP_LOAD_FLAGS (aiProcess_Triangulate\\
 | aiProcess_GenSmoothNormals\\
 | aiProcess_GenBoundingBoxes\\
 | aiProcess_JoinIdenticalVertices\\
 | aiProcess_FlipUVs\\
 | aiProcess_ConvertToLeftHanded\\
 | aiProcess_LimitBoneWeights)	

其中：

1、aiProcess_Triangulate：表示将导入的模型所有的面都转换为三角形；

2、aiProcess_GenSmoothNormals：表示强制产生光滑的法线；

3、aiProcess_GenBoundingBoxes：表示生成一个AABB的box，这个在碰撞检测时非常有用；

4、aiProcess_JoinIdenticalVertices：表示通过索引缓冲区的方式来引用顶点，并且相同的顶点只出现一次，剩下的交给索引。这对现代的显卡渲染来说具有较好的性能优势，这样对相同的顶点，顶点Shader只运行一次，当然可能被索引了多次；

5、aiProcess_FlipUVs：表示翻转一下纹理的UV坐标，对于通常的右手坐标系的模型使用了aiProcess_ConvertToLeftHanded标志做了翻转，对应的纹理坐标也需要通过这个标志翻转一下；

6、aiProcess_ConvertToLeftHanded：就是将模型翻转为D3D习惯的左手坐标系；

7、aiProcess_LimitBoneWeights：这个标志限制每个顶点最多能够被4个骨骼影响，实质上对于动画效果来说这已经足够了。好多模型动画数据中，由于建模软件计算的原因，有些顶点可能不止被4个骨骼影响。设置此标志可以限制顶点受其影响的骨骼数量，方便在Shader中固化顶点中关联骨骼数据大小，这会优化上传顶点数据的带宽。

  以上这些标志对于用D3D12进行基本的3D动画渲染就足够了。

4、网格（Mesh）

  在之前的系列教程中都没有详细讨论过关于渲染素材方面的话题，或者说对被渲染的物体如何表示之类的知识，比如网格（Mesh）数据结构、纹理（Texture）结构等都没有细讨论过。而这些对于基本的渲染来说，无论最终使用什么接口来进行渲染，都是必备的基础知识。

  现实世界中，大多数可见物体是因为可以反射光线进入人类的眼睛，从而使我们可以看到这些物体，而有些物体就不会反射光，比如空气，因此基本上我们是看不见空气的（大气层中臭氧层的天蓝色主要也是因为光线散射的原因，并不是反射，总之更准确的说应该是因为光线射入了我们的眼睛，才引起了我们视觉）。至于整个电磁波段啥都不反射的暗物质，作为低级文明的我们目前几乎是一无所知的。

  所以在渲染中，虚拟的3D场景中基本上放置的都是可以明确反射光线的物体（而对于透明或半透明的物体也是按照部分反射及透射光线的方式处理的，这些物体也会有“表面”，最终的目的任然是试图演算出最终射入人类眼睛的光线颜色）。而对于大多数反光物体来说，其实只是它的表面在反光，所以仅需要模拟其表面即可，而其内部就无须去模拟了，因为物体的内部根本就看不到，所以真正的3D渲染大致上就是一个给万事万物“画皮”的过程：

  也就是说只需模拟物体表面的反光特性欺骗过人类孱弱的眼睛基本就达到目的了，也就可以让大家看到所谓“3D”真实感的世界场景了。

  而这个“画皮”过程其实说白了就是用一个“向量几何表面”去“包裹”这个物体的过程。而由于世间万物的复杂性，就导致这张“包裹”物体的“皮”也就变的异常复杂，有些甚至是超复杂的曲面。当然这难不倒聪明的人类，因为无论多么复杂的“外表”，其实都是一个“2D的面”，而2D中最简单的图形就是三角形，与使用小的直线段首尾相接来模拟复杂的曲线类似，完全可以用最简单的三角形紧密相连，从而“拼凑”出任何复杂的“2D面”，这就是3D中经常使用的所谓三角形网格模型的本质。

  在计算机中具体表达这些三角形时，无非就是需要3个代表其顶点位置的向量即可。但是当三角形“首尾相接”甚至“接踵摩肩”的“拼凑”在一起时，就会发现其中好多顶点是多个三角形共用的，这时如果还是简单的为每个三角形重复提供顶点向量，就显得不那么“计算机专业”了。

  比如图中的P2-P3顶点就是两个三角形共用的。此时程序员们都会想到一个“自然而然”的方法，那就是把所有的顶点向量无重复的存储在一个数组中，然后用指向数组的索引号来表示每个三角形，这样就可以省下好多内存，而且性能上不但不会有什么损失，反而也会有一些提升，首先因为索引数组元素的计算时间复杂度是

O

(

1

)

\\mathbb{O}(1)

O(1)

  通常一个顶点向量需要3个浮点数来表示，而每个浮点数是4个字节，这样一个顶点至少都需要12个Byte的开销。而索引号通常可以用一个无符号短整型数unsigned short来表示，此时引用一个顶点只需要2Bytes，当然短整型有上限的限制，即每个“表皮三角形”中的顶点数不能超过64K，对于一般的网格来说这足够了，但是对于现代的复杂的网格，比如Unreal5中的那种超复杂的扫描现实世界得到的网格，就需要使用unsigned int来表示索引了。此时一个顶点的索引也只是占用了4Bytes，仍然远远小于每个顶点的12 Bytes。

  如上图中的简单网格就会形成如下的两个数组来表示：

  其中顶点的数组就是示例程序中的Vertex结构体数组，而第二个数组就是程序中的Index数组。大家可以试着计算一下这个简单的例子中节约了多少内存。

  关于网格，这里需要大家进一步理解下面几点：

  1、并不是说“2D面”就一定是平面，这里“2D”的含义是说仅用2个坐标就可以表示这个“面”上任意一点，但这个坐标往往不是简单的平面上的2D坐标。这也是纹理贴图坐标仅用UV两个坐标即可表示的原因。当然这个理解起来有点抽象，它隐藏了“2D面”可能是一个曲面甚至是闭合曲面的前提条件。用两个坐标即可表示任意2D面，其实是一个“拓扑表示”。形象的理解，比如地球上任意一点，在规定了南北极、赤道、本初子午线的条件下，都可以只用经纬度两个坐标就可以定义地球上任意一点，当然前提是已知地球是一个球体，如果假设地球是个“甜甜圈”形状，那么就需要另外规定坐标系统了，此时经纬度的含义（坐标函数）也就完全变了。

  2、往往这种表示还严格假设地球是一个近似完美球体的条件下，说经纬度坐标才有意义。如果再将这个经纬度按一定规则“平铺”到平面上，就得到了我们常见的地图。这种“2D面”的拓扑表示几乎可以简单的推广到任意3D虚拟物体上。而进一步这也是我们为3D模型进行纹理贴图的基础。当然这种拓扑变换后的平面图形一般都是变形的，这也提示我们，所谓“拓扑变换”（平铺）其实很多情况下是非线性的，因为这些“平铺”的图形无法通过简单的“线性”思考（即坐标的简单加减、放大或缩小计算等）还原为它们本来3D情景下的样子，所以导致纹理贴图的UV坐标也不是“纯线性”的坐标，但它确是连续的，注意“连续”不等同于“线性”！这也导致我们针对纹理坐标的很多计算往往是需要复杂的微积分（主要是微分）计算才能得到正确的结果。所以当你看到Sheder中有复杂的ddx、ddy等函数调用时就不要感觉到奇怪或无法理解了，因为纹理表面上是一张平面图片，但实际它本质上往往是一个复杂的几何体的表面，这时只能借助微分几何甚至几何拓扑的方法来计算它了。

  比如示例中人物模型的纹理贴图看上去就像下面这样：

  再比如地球的贴图：

  上面这些“拓扑”图片的最直观的感觉就是很多地方其实是被“扭曲”了，即图上的直线距离并不是在物体表面上的真实距离或“测地线”了。（提示：由此你可以进一步理解4维空间中有质量的球体拓扑到3维空间中时，其视见距离必定不是其4维空间中的真实距离了，因而其周边的时空也是“扭曲”的，而这就是爱因斯坦相对论引力的一个直观解释！颤抖吧孱弱的2维、3维生物们！）

  3、这种“拓扑变换”，往往也还是一种近似，即假设我们要“包裹”的3D物体近似为其规则的形状，从而忽略很多细节。所以如果只是简单的用这些拓扑后的图片作为纹理“包裹”到网格上之后，依然会看上去很假。比如对于地球我们就假设它是一个“完美的球体”，但其实真实的地球上是有高低起伏变化的复杂地形的。再比如值得我们骄傲的喜马拉雅山脉就不是平坦的，而且这种不平坦是很明显的。并且地球其实是一个两级稍扁而赤道稍鼓的不规则椭球体。再比如人体表面也并不是绝对光滑的，细节上其实至少还有丰富的毛孔等。如果要进一步更真实的模拟这些细节就需要使用辅助的表示细节的“法线贴图”、“位移贴图”等来帮忙。甚至在某些场景中，如复杂地貌的细节表示上，还需要“曲面细分”等技术手段，来进一步细致的近似出物体的表面。从而先从几何角度进一步使模拟光照效果更接近真实物体的光照的几何特性。如下图就是地球表面的“法线贴图”：

  下面是某个球体表面的“位移贴图”：

曲面细分的示例：

  4、实际的网格数据中，通常还会在顶点数据中存储很多附加属性信息，以表示真实物体在该点的丰富几何信息，比如：法线、切线、副切线、纹理坐标、顶点的颜色等。在本例中还会在顶点中存储顶点关联的骨骼信息。这些丰富的信息，最终的目的实质就是为了使物体在虚拟的光源场景情况下，尽可能反应出被模拟的物体表面的光反射特性，至少要保证光照在“几何”模拟上是正确的。从而使我们的眼睛被“欺骗”而认为是真的看到了被模拟的物体本身。而这些更丰富的顶点附加属性信息都会使得单个顶点的数据量会非常大，所以再简单的按照顶点被引用的顺序重复存储这些顶点数据就是非常不明智的了，此时前面说过的“索引”方式就显得非常重要了。因此复杂的虚拟物体网格几乎都是索引化的网格数据形式。这不但优化了存储，同时也提高了计算的性能，因为Vertex Shader会为每个顶点执行一遍，如果重复存储顶点了，那么因为重复计算必然导致计算量增大。当然优化存储后，虽然重复的顶点仅被执行一次，可能会引起不同的引用该顶点的三角形光照发生错误，但实际的情况中往往是这些“三角形”具有较好的“连续性”，几乎不会发生这样的错误。如果即使真的发生了这种明显的错误，那么只要美工进一步加入一些顶点，从而切分其中的一些三角形为更细致的三角形即可完全避免。下面HLSL代码片段即本示例中顶点的结构体定义：

struct VSInput
{
    float4 position : POSITION0;        //顶点位置
    float4 normal   : NORMAL0;          //法线
    float2 texuv    : TEXCOORD0;        //纹理坐标
    uint4  bonesID  : BLENDINDICES0;    //骨骼索引
    float4 fWeights : BLENDWEIGHT0;     //骨骼权重
};

  5、在用三角形表示物体的表面尤其是复杂曲面时，本质上因为三角形在欧式几何中其实是一个标准的平面形，并且计算机中都是按照欧式几何运算三角形的，所以最终只是一种用“无数”小平面去逼近曲面的情形。这与2000多年前我国伟大的数学家祖冲之用无限接近圆的正多边形去计算圆周率时的2D情形类似，只不过这里是用很多小平面三角形，而且基本都是不规则三角形去近乎无限的逼近3D物体的外形，从而保证最终的网格至少在几何特征上接近真实物体的外观特征。当然一些特殊情形下，这种表示几乎是完全等同的，比如规则的正方体、立方体等。


  总之，啰嗦这么多，主要是为了让大家从本质上理解三角形网格表示3D物体的过程，实质上就是一个“画皮”的近似过程。核心目的就是尽可能从几何的角度保证物体外观特征的正确性，从而进一步保证虚拟场景中的光照在几何上是“几乎正确的”，因为光照的过程首先是一个几何的过程。而在几何正确的基础上，才能再近似模拟光的其它物理特征，尤其是能量特征，而这就是现代渲染中流行的PBR光照了，最终整个场景看上去就几乎可以“乱真”了。

  关于网格基础知识及其他的知识我就不多啰嗦了，大家可以去阅读计算机图形学的相关内容来恶补这些知识，最终辅以这里的内容，我相信大家会完全理解网格模型的全部含义了。当然其中谈到了一些高级的数学概念，比如拓扑、微分几何等，如果你完全不了解，目前来说也没有太大关系，能通过本章的学习对这些数学知识有个感性认识基本也就可以应付至少80%以上的渲染编程问题了，所以不用过渡慌张和恐惧。当然如果有兴趣可以深入的了解一下这些数学知识，如果能完全掌握，那么你就可以轻松的撰写SIG（SIGGRAPH 2021）水平的论文了，也就不用看我啰里吧嗦的所谓教程了。

5、骨骼动画基础

  搞明白了“2D面”网格模拟3D物体的原理之后，接着让我们来思考怎么能让这个“静态”的网格进一步能够像真实世界中的物体那样动起来。这里的运动主要分为两大类，一类是说让网格整体动起来，比如汽车的前进、飞机的飞行等，这类运动主要靠常规的位移矩阵变换即可实现，如果加上物理模拟的考量，比如速度、加速度等，这类运动基本就是“刚体运动”，本章就不讨论了。而另一类运动就是需要网格自身进行一些“变形”运动了，比如，3D虚拟人物的走路动作、跑步动作、甚至射击、搏击动作等等，这类动作往往牵扯到网格内顶点的变换。当然还有一类比较特殊的动画，经常用于模拟漫天飞雪、火焰等等，被称之为“粒子”动画，严格来说，它只是说一次控制的小对象比较多，并且还要控制

  所谓网格内顶点的变换，说白了就是网格自身要发生某种“变形”，即网格上至少有一点相对于其它点要发生明显的位置改变。这类运动，根据采用的技术手段不同又可以分为两大类：一类就是本章将要重点介绍的依托“骨骼”的变形运动；另一类就是基于目标网格进行插值变换的变形运动，多用于人物面部表情变化，后续我们再介绍。


  “骨骼动画”的基本思路就是模拟人类或动物骨骼运动从而带动身体动作的过程。刚才我们已经介绍了网格实质是个“画皮”的过程，那么要让这张“皮”进一步动起来，就需要模拟其内部骨头的活动，然后带动表皮运动，这样从外表上看起来就是“画皮”动了起来，并且因为内部模拟的是人类或动物骨头的活动，所以整体看起来就与一个“真人”的活动并无二至了。所以骨骼动画也因此而得名。当然这个思路对于3D动画来说也是最简单直接和自然的一个方法。甚至对于一些没有骨骼的生物，比如章鱼、毛毛虫、昆虫之类在建模时也都人为的加上虚拟的骨骼，从而模拟出这类生物的动作。有些甚至干脆虚拟出类似人体的骨骼就拟人化形成了卡通形象。

  “骨骼动画”在具体表示上就是让网格上的顶点分组绑定到虚拟的类似骨骼状排列的具有树状结构的空间点（称为“骨骼”）上，当该“骨骼”依照时间点做相应变动时（就是依照时间轴生成变换矩阵），就会影响绑定到该点上的顶点以一个权重值（Weight）做相应的变动。最终所有骨骼都“动”起来之后，整个网格就依照规则“动”起来。从这个比较绕的描述上来看，其实骨骼动画主要有几个要素：网格、骨骼绑定、时间轴、骨骼变换矩阵、关联顶点及权重、变换顶点。基本的过程就是：骨骼绑定->根据动画序列遍历骨架生成每个骨骼（或关节）变换的矩阵->用变换矩阵变换受影响的顶点。

  由此也可以看出，骨骼动画中虚拟的骨骼实质上并不会形成类似“网格”那种最终可见的像素，本质上它最终就是一组组时间轴上的变换矩阵，但是为了建模的方便，很多3D动画建模软件中，都会将虚拟骨骼的局部坐标系原点链接起来加以显示，形成可视化的骨骼形象。这些原点通常是骨骼系统中的关节点，实质上骨骼能够自由运动的坐标系参考点就是诸多的关节点，所以以关节点作为局部坐标系的原点来表达骨骼的变换是具有天然的描述简单易理解的优势的。

  另外通常因为网格一般是3维结构，并且在动画中都必须要使用时间轴，所以有些时候有些夸张的宣传会将3D动画宣传为4D动漫，其实这种说法也比较合适，至少这提醒了我们，在计算骨骼动画的时候，必须要严格考虑时间轴的问题，即需要4D的思考能力，但这与4D向量啥的没有任何关系，这里只是说3D的网格+1D的时间轴变换=动画。（迪士尼乐园里的4D与这里说的不同，是将加入的真实环境反馈包括力反馈、水雾反馈、声音反馈等称之为4D动漫。）