10、动画关键帧解算

在本章示例中，对导入后的模型动画数据，主要通过两个函数：CalcAnimation和递归函数ReadNodeHeirarchy，以及其它辅助工具函数来完成。

10.1、时间轴

对于动画、音乐、视频等，甚至游戏引擎来说，正确的时间轴是一切逻辑运行正确的基础前提。本例中，没有使用高性能高精度的时间函数，而是使用了普通版的GetTickCount的64位版本，时间精度只有毫秒（ms）级，但这不影响本章动画加载渲染演示程序的运行，基本上也够用了。在正式的项目、引擎或产品中推荐使用QueryPerformanceCounter等函数。

本示例中的时间轴逻辑不复杂，就不多赘述了。只是需要提醒的是注意最后一个换算，正常的应该是除以1000换算成秒数，但我在实际加载和演示一些x类型文件时，发现如果那样的话会引起动画播放过快的问题，所以调试几轮下来以后，改做了除以5，以使动画播放速度正常。正式的代码中，这种“变速”问题一定要放到模型动画解算中去处理，而不能放在全局消息循环中！

FLOAT fStartTime = ( FLOAT )::GetTickCount64();
FLOAT fCurrentTime = fStartTime;
FLOAT fTimeInSeconds = ( fCurrentTime - fStartTime ) / 1000.0f;

// 16、消息循环
fCurrentTime = ( FLOAT )::GetTickCount64();
//fTimeInSeconds = (fCurrentTime - fStartTime) / 1000.0f;
fTimeInSeconds = ( fCurrentTime - fStartTime ) / 5.0f;

10.2、遍历动作CalcAnimation

如前所述，在Assimp加载的模型数据中，关键帧数据被放在aiScene::mAnimations对象数组中，每一个数组成员即代表一个完整动作中所有相关骨骼的全部关键帧数据，所以动画实际播放时，一定要记录当前播放的数组索引号（stMeshData.m_nCurrentAnimIndex），也就是当前播放动作索引。对于复杂的角色模型来说，有十几套甚至几十套完整动作是很常见的，但更多更复杂的动作集合也往往意味着更高的造价！

当根据索引找到当前需要播放的动作数据后，接着就是重要的Tick解算。Tick可以理解为一个频率值，即一个动作每秒钟播放多少个关键帧，然后需要将当前秒数乘以Tick值（fTimeInSeconds * TicksPerSecond），并对整个动画持续时间值（pAnimation->mDuration）取余（fmod(TimeInTicks, (FLOAT)pAnimation->mDuration);），即得到当前需要播放哪一个关键帧。因为这个值往往不太可能恰好落在某个关键帧的时间点上，常常会落在某两个关键帧之间，所以最终需要在两个关键帧之间进行变换插值。

确定了最终需要“播放”的动画的关键帧的“时间点”，就可以根据“骨架”，通过调用ReadNodeHeirarchy递归遍历计算当前动画的所有骨骼变换矩阵了。

VOID CalcAnimation(ST_GRS_MESH_DATA& stMeshData
                   , FLOAT fTimeInSeconds
                   , CGRSARMatrix& arTransforms)
{
	XMMATRIX mxIdentity = XMMatrixIdentity();
	aiNode* pNode = stMeshData.m_paiModel->mRootNode;
	aiAnimation* pAnimation 
        	= stMeshData.m_paiModel->mAnimations[stMeshData.m_nCurrentAnimIndex];

	FLOAT TicksPerSecond = (FLOAT)(pAnimation->mTicksPerSecond != 0
		? pAnimation->mTicksPerSecond
		: 25.0f);

	FLOAT TimeInTicks = fTimeInSeconds * TicksPerSecond;
	FLOAT AnimationTime = fmod(TimeInTicks, (FLOAT)pAnimation->mDuration);

	ReadNodeHeirarchy(stMeshData, pAnimation, AnimationTime, pNode, mxIdentity);

	UINT nNumBones = (UINT)stMeshData.m_arBoneDatas.GetCount();

	for (UINT i = 0; i < nNumBones; i++)
	{
		arTransforms.Add(stMeshData.m_arBoneDatas[i].m_mxFinalTransformation);
	}
}

10.2、递归遍历骨骼树ReadNodeHeirarchy

ReadNodeHeirarchy函数，是个比较老套的“先根序”“骨架”树结构递归遍历算法。
在这里插入图片描述
首先，需要将当前骨骼的默认变换矩阵（pNode->mTransformation）读取出来，依据D3D祖传左手坐标系的习惯，需要做个转置先。接着根据当前骨骼名称，查找（FindNodeAnim）动画数据中对应的关键帧节点。如果没有找到，其实按照之前所述，这往往表示当前骨骼可能是个“匿名”节点，仅作为“骨架”中的中间过渡连接节点，其默认变换矩阵即等于该骨骼最终的变换矩阵。

如果找到了当前骨骼对应的动画关键帧数组数据（Assimp中称为"通道mChannels"），那么根据“时间点AnimationTime”，先找到对应的关键帧数据元素，必要时进行插值，计算出该骨骼在当前帧需要的基本变换（SQT）：缩放、旋转、位移对应的分量，再按D3D祖传左手坐标系顺序进行“变换复合”（OpenGL是相反的顺序，又因为我们直接使用的DirectXMath库，所以就不需要转置操作了）,然后按顺序把矩阵乘起来（mxNodeTransformation = mxScaling * mxRotationM * mxTranslationM; ），最后用这个矩阵替代当前骨骼的变换矩阵，作为骨骼最终的变换矩阵。

接着，将当前骨骼变换矩阵乘以其父骨骼的变换矩阵（ mxGlobalTransformation = mxNodeTransformation * mxParentTransform），就得到了当前骨骼相对于整个模型空间的变换矩阵。然后根据骨骼名称，找到之前所述的骨骼数组中当前骨骼对应的元素索引，先将数组中的“逆位姿绑定矩阵”乘以一个当前骨骼变换矩阵再乘以整个模型的变换矩阵:

stMeshData.m_arBoneDatas[nBoneIndex].m_mxFinalTransformation
= stMeshData.m_arBoneDatas[nBoneIndex].m_mxBoneOffset
* mxGlobalTransformation 
* stMeshData.m_mxModel;

就得到了最终的骨骼相对于世界空间中的变换矩阵。

void ReadNodeHeirarchy(ST_GRS_MESH_DATA& stMeshData
	, const aiAnimation* pAnimation
	, FLOAT AnimationTime
	, const aiNode* pNode
	, const XMMATRIX& mxParentTransform)
{
	
	XMMATRIX mxNodeTransformation = XMMatrixIdentity();
	MXEqual(mxNodeTransformation, pNode->mTransformation);
	mxNodeTransformation = XMMatrixTranspose(mxNodeTransformation);

	CStringA strNodeName(pNode->mName.data);

	const aiNodeAnim* pNodeAnim = FindNodeAnim(pAnimation, strNodeName);

	if ( pNodeAnim )
	{
		// 缩放
		XMVECTOR vScaling = {};
		CalcInterpolatedScaling(vScaling, AnimationTime, pNodeAnim);
		XMMATRIX mxScaling = XMMatrixScalingFromVector(vScaling);

		// 四元数旋转
		XMVECTOR vRotationQ = {};
		CalcInterpolatedRotation(vRotationQ, AnimationTime, pNodeAnim);
		XMMATRIX mxRotationM = XMMatrixRotationQuaternion(vRotationQ);

		// 位移
		XMVECTOR vTranslation = {};
		CalcInterpolatedPosition(vTranslation, AnimationTime, pNodeAnim);
		XMMATRIX mxTranslationM = XMMatrixTranslationFromVector(vTranslation);

		// 骨骼动画中 最经典的 SQT 组合变换
		mxNodeTransformation = mxScaling * mxRotationM * mxTranslationM; 
	}

	XMMATRIX mxGlobalTransformation = mxNodeTransformation *  mxParentTransform;

	UINT nBoneIndex = 0;
	if (stMeshData.m_mapName2Bone.Lookup(strNodeName, nBoneIndex))
	{
		stMeshData.m_arBoneDatas[nBoneIndex].m_mxFinalTransformation
			= stMeshData.m_arBoneDatas[nBoneIndex].m_mxBoneOffset
			* mxGlobalTransformation 
			* stMeshData.m_mxModel;
	}

	for (UINT i = 0; i < pNode->mNumChildren; i++)
	{
		ReadNodeHeirarchy(stMeshData
			, pAnimation
			, AnimationTime
			, pNode->mChildren[i]
			, mxGlobalTransformation);
	}
}

当前骨骼的最终世界空间变换矩阵计算出来后，首先存储到全局骨骼矩阵数组元素的成员中（stMeshData.m_arBoneDatas[nBoneIndex].m_mxFinalTransformation），接着就是循环递归遍历当前骨骼的子骨骼数组，并将这个矩阵作为子骨骼的父骨骼矩阵传入，因为所有骨骼的变换都是相对于自己的局部坐标系设定的，所以计算最终变换时，需要使用父骨骼的变换矩阵将自己变换到父骨骼的坐标空间中。这样“骨骼树”的最终含义就明确了，其实它就是骨骼的子坐标空间的层层级联。

最后需要注意的是stMeshData.m_mxModel，这个模型的最终变换矩阵，本章示例中直接来自于模型导入数据中的根节点的变换矩阵，这个矩阵往往被设定为一个单位矩阵。当需要对模型进行进一步的整体变换时，还需要若干变换（缩放、旋转、位移等）矩阵继续右乘这个矩阵。

10.3、关键帧数据解算和插值

关键帧数据的解算，在本章示例中其实就是一个数组线性查找过程。

具体的，首先根据骨架中具体的骨骼名称找到对应的动画通道数据，也就是该骨骼对应的完整动作的关键帧数组：

const aiNodeAnim* FindNodeAnim(const aiAnimation* pAnimation, const CStringA strNodeName)
{
	for (UINT i = 0; i < pAnimation->mNumChannels; i++)
	{
		if ( CStringA(pAnimation->mChannels[i]->mNodeName.data) == strNodeName)
		{
			return pAnimation->mChannels[i];
		}
	}
	return nullptr;
}

接着要判断一下aiNodeAnim* pNodeAnim（即pAnimation->mChannels，通道）中是否有多帧数据，也就是说看看这个数组元素数量是否大于1，根据Assimp的约定，一般情况下如果pAnimation->mChannels对应元素的指针不为空，那么至少都会有1帧变换数据，所以不会有0个元素的情况出现。如果是1帧数据的，那么就不管AnimationTime值，而直接返回这一帧数据即可。

在aiNodeAnim中，每组变换数据：缩放、旋转、位移都是分开存放的。一般情况下，这三个数组的大小是一致的，也就是说每一帧中都同时拥有这三个变换的数据，这也是一般的关键帧骨骼动画的基本要求。但要注意的是，并不总是这样。所以示例代码中也是分开这三个变换数据来处理的。而处理的逻辑基本都是一致的，即先查找对应AnimationTime时间点对应变换数据的数组索引（注意特殊设计的查找，总是保证找到的索引值小于数组上限-1，总是使得下一索引有效！)，再根据当前帧索引（PositionIndex），+1得到下一帧索引（NextPositionIndex），计算两帧之间的时间差（DeltaTime），接着利用AnimationTime-当前帧的时间点值（pNodeAnim->mPositionKeys[PositionIndex].mTime），然后除以刚才计算得到的时差（DeltaTime）值，就得到了在两帧之间插值的t值（Factor）。最后利用对应的线性插值函数，在两帧各自的变换数据之间根据Factor值进行插值。

void CalcInterpolatedPosition(XMVECTOR& mxOut
                              , FLOAT AnimationTime
                              , const aiNodeAnim* pNodeAnim)
{
	if (pNodeAnim->mNumPositionKeys == 1)
	{
		VectorEqual(mxOut, pNodeAnim->mPositionKeys[0].mValue);
		return;
	}

	UINT PositionIndex = 0;
	if (! FindPosition(AnimationTime, pNodeAnim, PositionIndex))
	{// 当前时间段内没有位移的变换，默认返回0.0位移
		mxOut = XMVectorSet(0.0f,0.0f,0.0f,0.0f);
		return;
	}

	UINT NextPositionIndex = (PositionIndex + 1);

	ATLASSERT(NextPositionIndex < pNodeAnim->mNumPositionKeys);
    
	FLOAT DeltaTime 
        = (FLOAT)(pNodeAnim->mPositionKeys[NextPositionIndex].mTime 
                  - pNodeAnim->mPositionKeys[PositionIndex].mTime);
	FLOAT Factor 
        = (AnimationTime - (FLOAT)pNodeAnim->mPositionKeys[PositionIndex].mTime) / DeltaTime;
    
	ATLASSERT(Factor >= 0.0f && Factor <= 1.0f);

	VectorLerp(mxOut
		, pNodeAnim->mPositionKeys[PositionIndex].mValue
		, pNodeAnim->mPositionKeys[NextPositionIndex].mValue
		, Factor);
}

void CalcInterpolatedRotation(XMVECTOR& mxOut, FLOAT AnimationTime, const aiNodeAnim* pNodeAnim)
{
	if (pNodeAnim->mNumRotationKeys == 1)
	{
		QuaternionEqual(mxOut, pNodeAnim->mRotationKeys[0].mValue);
		return;
	}

	UINT RotationIndex = 0;
	if (!FindRotation(AnimationTime, pNodeAnim, RotationIndex))
	{// 当前时间段内没有旋转变换，默认返回0.0旋转
		mxOut = XMVectorSet(0.0f,0.0f,0.0f,0.0f);
		return;
	}

	UINT NextRotationIndex = (RotationIndex + 1);
	ATLASSERT(NextRotationIndex < pNodeAnim->mNumRotationKeys);
	FLOAT DeltaTime = (FLOAT)(pNodeAnim->mRotationKeys[NextRotationIndex].mTime
		- pNodeAnim->mRotationKeys[RotationIndex].mTime);
	FLOAT Factor = (AnimationTime - (FLOAT)pNodeAnim->mRotationKeys[RotationIndex].mTime) / DeltaTime;
	ATLASSERT(Factor >= 0.0f && Factor <= 1.0f);

	QuaternionSlerp(mxOut
		, pNodeAnim->mRotationKeys[RotationIndex].mValue
		, pNodeAnim->mRotationKeys[NextRotationIndex].mValue
		, Factor);

	XMQuaternionNormalize(mxOut);
}

void CalcInterpolatedScaling(XMVECTOR& mxOut, FLOAT AnimationTime, const aiNodeAnim* pNodeAnim)
{
	if ( pNodeAnim->mNumScalingKeys == 1 )
	{
		VectorEqual(mxOut, pNodeAnim->mScalingKeys[0].mValue);
		return;
	}

	UINT ScalingIndex = 0;
	if (!FindScaling(AnimationTime, pNodeAnim, ScalingIndex))
	{// 当前时间帧没有缩放变换，返回 1.0缩放比例
		mxOut = XMVectorSet(1.0f, 1.0f, 1.0f, 1.0f);
		return;
	}

	UINT NextScalingIndex = (ScalingIndex + 1);
	ATLASSERT(NextScalingIndex < pNodeAnim->mNumScalingKeys);
	FLOAT DeltaTime = (FLOAT)(pNodeAnim->mScalingKeys[NextScalingIndex].mTime - pNodeAnim->mScalingKeys[ScalingIndex].mTime);
	FLOAT Factor = (AnimationTime - (FLOAT)pNodeAnim->mScalingKeys[ScalingIndex].mTime) / DeltaTime;
	ATLASSERT(Factor >= 0.0f && Factor <= 1.0f);

	VectorLerp(mxOut
		, pNodeAnim->mScalingKeys[ScalingIndex].mValue
		, pNodeAnim->mScalingKeys[NextScalingIndex].mValue
		, Factor);
}

关于Scale变换、Position变换的线性插值比较容易理解，最终使用DirectXMath库中的向量线性插值函数XMVectorLerp即可（为了方便兼容Assimp，做了简单封装，即函数VectorLerp）。而对于旋转变换（即Quaternion四元数，按前面所述，其实理解为方位变换更合适），则使用了四元数的球面线性插值，同样DirectXMath中也为我们准备了对应的函数XMQuaternionSlerp（一样做了简单封装，即函数QuaternionSlerp）。

最后关键帧搜索函数的代码如下：

BOOL FindPosition(FLOAT AnimationTime, const aiNodeAnim* pNodeAnim, UINT& nPosIndex)
{
	nPosIndex = 0;
	if (!(pNodeAnim->mNumPositionKeys > 0))
	{
		return FALSE;
	}

	for ( UINT i = 0; i < pNodeAnim->mNumPositionKeys - 1; i++ )
	{
		// 严格判断时间Tick是否在两个关键帧之间
		if ( ( AnimationTime >= (FLOAT)pNodeAnim->mPositionKeys[i].mTime )
			&& ( AnimationTime < (FLOAT)pNodeAnim->mPositionKeys[i + 1].mTime) )
		{
			nPosIndex = i;
			return TRUE;
		}
	}

	return FALSE;
}

BOOL FindRotation(FLOAT AnimationTime, const aiNodeAnim* pNodeAnim, UINT& nRotationIndex)
{
	nRotationIndex = 0;
	if (!(pNodeAnim->mNumRotationKeys > 0))
	{
		return FALSE;
	}

	for (UINT i = 0; i < pNodeAnim->mNumRotationKeys - 1; i++)
	{
		// 严格判断时间Tick是否在两个关键帧之间
		if ( (AnimationTime >= (FLOAT)pNodeAnim->mRotationKeys[i].mTime )
			&& (AnimationTime < (FLOAT)pNodeAnim->mRotationKeys[i + 1].mTime) )
		{
			nRotationIndex = i;
			return TRUE;
		}
	}

	return FALSE;
}

BOOL FindScaling(FLOAT AnimationTime, const aiNodeAnim* pNodeAnim, UINT& nScalingIndex)
{
	nScalingIndex = 0;
	if (!(pNodeAnim->mNumScalingKeys > 0))
	{
		return FALSE;
	}

	for (UINT i = 0; i < pNodeAnim->mNumScalingKeys - 1; i++)
	{
		// 严格判断时间Tick是否在两个关键帧之间
		if ( ( AnimationTime >= (FLOAT)pNodeAnim->mScalingKeys[i].mTime )
			&& ( AnimationTime < (FLOAT)pNodeAnim->mScalingKeys[i + 1].mTime) )
		{
			nScalingIndex = i;
			return TRUE;
		}
	}
	return FALSE;
}

上面的搜索代码可能会出问题，即当倒数第一帧的时间点mTime值刚好等于或大于AnimationTime时，可能会错误的返回索引0，从而使得动画又从头开始，导致动画出现“跳跃”感。正常情况下，这种情况不会出现，因为AnimationTime再传入时，已经对整个动画持续时间（pAnimation->mDuration）做了取余操作（fmod(TimeInTicks, (FLOAT)pAnimation->mDuration);），所以不会出现这样的错误。但不排除有些模型中，可能动画持续时间与具体的帧的总时间点不一致而导致此问题。此时可以考虑使用最后帧的mTime值取代mDuration值，对TimeInTicks做取余操作。

10.4、生成关键帧骨骼变换矩阵

计算得到插值帧基本变换“向量”后，就是要使用这些“向量”来生成对应的变换矩阵。幸运的是DirectXMath库中同样为我们封装好了这些函数，只需要调用一下即可：

// 缩放
XMVECTOR vScaling = {};
CalcInterpolatedScaling(vScaling, AnimationTime, pNodeAnim);
XMMATRIX mxScaling = XMMatrixScalingFromVector(vScaling);

// 四元数旋转
XMVECTOR vRotationQ = {};
CalcInterpolatedRotation(vRotationQ, AnimationTime, pNodeAnim);
XMMATRIX mxRotationM = XMMatrixRotationQuaternion(vRotationQ);

// 位移
XMVECTOR vTranslation = {};
CalcInterpolatedPosition(vTranslation, AnimationTime, pNodeAnim);
XMMATRIX mxTranslationM = XMMatrixTranslationFromVector(vTranslation);

// 骨骼动画中 最经典的 SQT 组合变换
mxNodeTransformation = mxScaling * mxRotationM * mxTranslationM; 
// OpenGL：TranslationM* RotationM* ScalingM;

10.5、关于性能的一些考虑

关于整个动画数据的解算过程就介绍完毕了，虽然这个过程很“经典”，但本章示例中的代码基本上还是按照Assimp导入数据的结构来设计的算法，基本上保持了一种“原汁原味”“经典”的味道，这样做的目的即让大家能够轻松并且牢固的掌握骨骼动画计算的整个过程及基本原理。

实际的正式代码中，这个过程需要做很多优化，具体的优化方法，就不多说了，以防内容太多，分散精力导致大家学习效果的下降。这里只提几个基本的思路：

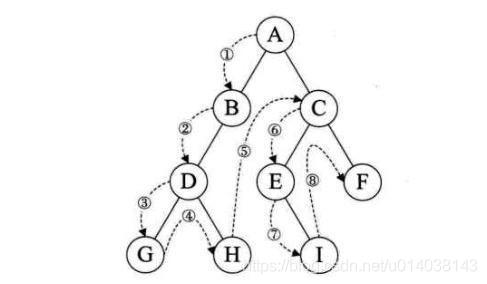
1、之前的篇章中已经说过，可以将Assimp导入的模型数据理解为是一种中间数据（ID），那么这其实也是说，我们完全可以按照提高性能的要求来设计对应的自有格式的数据结构来做一次“预转换”，比如将树形结构的“骨架树”拆分为线性结构，并且将分离在骨架（aiNode树）以及aiAnimation中的信息整合为一个完整的信息，不需要每次都去根据名称查找每组数据。（如下图，使用先序遍历的线性结构存储即可，当然要反过来在子节点中存储父节点的指针，方便级联的计算。）
在这里插入图片描述
2、如果上述的树形结构转线性结构完成了，剩下的就是可以将遍历骨骼树的递归算法，直接变成了线性算法，时间复杂度将大大降低。

3、对于根据时间点查找帧的过程，可以直接考虑换做“二分查找”等快速查找算法，因为最终动画关键帧数据一般是根据时间点从小到大有序排放的，所以要完全利用数据的这种天然结构性。

总之，上述优化思路的核心思想就是说，要优化算法，先优化数据结构，然后充分利用数据结构中其它的一些天然属性，比如：有序性，等差数列，等比数列，闭包等等，来优化算法。当然这种思想，更有利于应用于实际优化算法和写代码中，而不利于设计算法，因为设计算法之前你根本不知道最终算法是什么样子，也就无从谈起找到更有效的数据结构。

关于动画解算过程的优化是很有意义的，因为动画解算部分基本上都是在CPU端完成的，并且是需要每帧都重新计算一遍，所以如果想在一个游戏中或者别的需要3D动画渲染的程序中加入多样的复杂的动画角色，那么就需要优化动画的解算过程，从而节约宝贵的CPU资源。当然我们也已经介绍过了多线程渲染的方法，解算动画的过程也可以放在多线程中分开处理，但严格来讲这种优化只能是编程技巧级别的优化，算法本身并没有优化，只是相当于让问题规模参数n缩小了常数倍而已，算法的时间复杂度并没有本质的变化。但这也并不是说多线程渲染就毫无意义了，因为大多数实际情况中，问题规模参数n，在这里也就是动画总数量、帧数、骨骼数量等参数，可能都很小，当对它除以一个较大的常数时，最终每个线程需要处理的问题规模参数n就可能很小了，所以性能的实际改观还是很可观的。（现在已经有128线程的“线程撕裂者”CPU了，假设你正好有128个不同角色动画要解算，这时每个线程实质上只需要解算1个动画！）
在这里插入图片描述

11、骨骼调色板

所有动画解算完毕后，其实就是得到了一个对应每个骨骼相对于世界坐标系（或模型空间更准确）中的全局变换矩阵（一般是相对于整体模型空间的，本例中没有后续的进一步变换，所以等同于直接变换到了世界空间中）组成的数组，在本章示例中，就是计算得到了一个类型为：

typedef CAtlArray<XMMATRIX> CGRSARMatrix;

的数组。

最后使用该数组，去填充常量缓冲区，对应到shader中的“骨骼动画调色板”结构（就是变换矩阵数组）：

cbuffer cbBones : register(b1)
{
    float4x4 mxBones[256];              //骨骼动画“调色板” 最多256根"大骨头"。内存大，显存多，任性！
};

需要注意的是，在shader中目前只能使用静态数组，所以必须在定义时明确指定数组的大小。如本章示例代码中上述shader所示，定义了一个有256个矩阵的数组，其实这对于一般的动画包括稍复杂点的动画已经足够了，有些情况下实际定义到80个或者40个也就足够了，因为这个数组大小实际等同于模型中最大骨骼数量，一般的模型中不会设计过多的骨骼（关节），而是通过丰富模型的“动作”（理解为对应aiAnimation数组大小）以及精细化关键帧数据（理解为对应aiAnimation::mChannels数组大小）来改善最终动画的呈现效果的，并不是通过增加骨骼（关节）来改善。

文章版权归作者所有，未经允许请勿转载。

THE END