6、实时PBR

  如果你耐心的读到了这里，那么请给自己点个赞先。基本的物理的方程，相信大家应该有所了解了，只是可能计算的过程还有点模糊。其实无论实时PBR还是非实时PBR，都是首先计算光源，再从光源计算光线在场景中各种反射、散射、折射等过程照亮场景，然后将得到的光照颜色信息按照位置填充到2D图像对应的像素点中即可，整个计算过程并没有牵扯到物体的实际几乎信息等。

  或者更直接的说，PBR主要在Pixel Shader中实现，在OpenGL中是在Frame Shader中实现。因此PBR渲染几乎可以适用于所有的渲染方式或渲染管线中，即可以用在光追渲染中，也可以用在普通光栅化渲染中，还可以应用于延迟渲染或者Forward+渲染中等等。

  当然实际的计算中这个过程往往是反过来的，尤其是在光线追踪中（参看：光线追踪渲染（RayTracing Render）核心原理详解 ），这个过程是反其道而行之的，也就是从虚拟的摄像机，投射到2D虚拟屏幕上的一个像素点，再从像素点投射到场景物体上的某个点，然后最终通过复杂的反射折射到达光源而已，而PBR计算就发生在“碰撞到”的物体表面这个点上。那么为什么这个过程可以反过来呢？先不说反过来之后节约了大量的计算开销（看光追原理中的介绍），其实最最核心的原因就是因为BRDF都是“双向”的，也就是说你从入射端计算或者从出射端计算都是一样的。这对于光栅化渲染的过程也是一样的，只是说光栅化时，往往像素点的颜色来自于Z缓冲中对应深度最小的物体表面的点而已，计算其实是从物体表面的点开始的，说到这里大家还可以继续自行脑补一下光栅化计算的时候有没有计算的浪费？（关于这个问题，有兴趣的同学可以学习下延迟着色技术等，之后我看如果有精力就做几个相关的demo再写几篇教程）。

  同时也因为BRDF的或者BxDF系列函数的双向性，所以使得PBR渲染几乎在所有的光照环境中都表现的是我们预期的那样，或者说表现的都是高度“一致的”。或者更直白的说，使用PBR渲染，你只需要设定一次物体表面的BRDF及相关参数，那么最终无论物体位置或物体间位置以及光源位置等如何变化，最终物体表面表现出的光照效果都是一样的，而在传统光照这种变化在一些特殊情况下往往会引起一些“失真”现象，根本原因其实是因为传统光照没有考虑能量守恒导致的。

  OK，在这里我们就先不纠结计算顺序的问题了，核心就是大家一定要搞明白我们到底计算些啥？首先我们需要计算的是光源，也就是说获得光源的RGB值。其次是根据光源光照计算虚拟场景中3D物体表面的反射方程算出出射的光线，最后就是根据出射的光线点亮2D屏幕上的某个像素点。

6.1、PBR渲染

  实际中判断一种PBR光照模型是否是基于物理的，必须满足以下三个条件：

a、基于微平面(Microfacet)的表面模型

  对于每个微分点p将其抽象为一个极微小的平面，只是其上任然有结构，比如是否光滑的，还是充满了皱着。这主要是因为相对于微表面来说，实际可能就是屏幕上一个像素的大小来说，光子都是无穷小的存在，所以入射其上的光子数量任然是“巨量”的，即积分时需要考虑的

d

ω

i

d \\omega_i

dωi​ 是非常非常多的，而每个入射到该点或像素上的光子仍然可能会因为微表面上的一些影响而发生不同方向的反射或透射。

b、遵循能量守恒定律

  这个在前面已经讲过了。

c、应用基于物理的BRDF函数

  这个是自然而然的要求，不论什么样的渲染场景，大多数主题内容都是基于现实世界场景的模拟表达，其中的大多数物体在现实中都有对应物，渲染的终极目标就是为了让这些虚拟物与现实中的物品至少是“看上去一致”的，或者直白的说，就是“金属”必须看上去是“金属”，而“塑料”就是“塑料”等等，这时要注意的是具体物体是要表达什么物体是物体网格模型的事情。当然还需要注意的是我们使用的一定是“线性”的BRDF函数，因为非线性无法根本上保证能量守恒，从而导致失真。

6.2、光源

  之前在讨论辐照度的时候，已经说过了，实时PBR与非实时PBR的第一个分水岭就是对光源的计算，当然这里说的光源不只是说能够自发光的物体，还包括一个物体反射出来的光，二次入射到别的物体表面等，而这样的物体也可以被看做光源。

  这样的计算也更复杂，因为首先需要计算反光物体表面反光的全部出射辐照度作为被照射物体的入射辐照度之一，再次整个计算过程还需要考虑复杂的能量守恒关系。这样一来二次反射可以进一步递归形成高次反射，只是在实时PBR中有些递归被大大简化了，甚至忽略掉了，往往只是特意安排计算下场景中指定的一些所谓“高光”物体的二次或高次反射即可，比如光亮的玻璃，高光金属表面等等。

  对于非实时PBR来说，这通常都是需要用类似光追渲染（需要注意的是基本上非实时PBR都是基于光线追踪的渲染）进行所谓路径跟踪（Path Tracing）之后确定物体之间复杂的反射照射关系后再来根据路径进行复杂的迭代计算的，过程中每个光线碰撞点都需要根据BRDF做至少一次积分计算，其运算量是非常巨大的。（目前在Shader Model 6.6中开放了在传统光栅化渲染Shader中使用光线追踪Shader API的能力，这使得我们可以在光栅化渲染中快速高效的利用 ray tracing 的能力，也就是现代GPU的硬件能力来进行路径追踪 path tracing，从而进行高次反射计算的模拟，从而进一步提高画质。这个后续看有机会我们再详细介绍。）

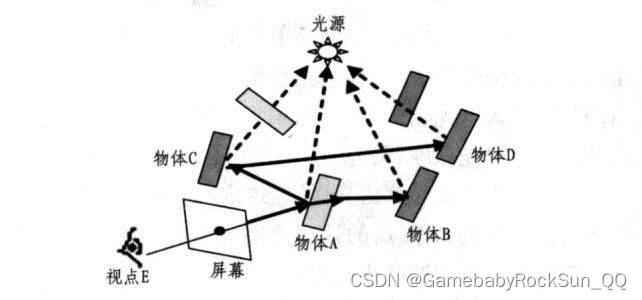
  对于直接光源的计算来说，在实时PBR中，根据之前的讨论，其实就是简单获取光源的RGB颜色即可，或者直接对整个复杂场景中获取一张“环境映射”作为光源即可，有时候还会对光源表面建模形成特殊的光源纹理，这些作为光源的纹理往往就是一副HDR纹理，其中包含了丰富的光源或光照能量信息，一般都是HDR格式的，也就是RGB值都会远大于1.0f。与漫反射纹理不同，光源纹理中每个像素都代表一个光源上或物体上的出射辐射度，最后根据入射立体角积分作为物体表面的入射辐照度或一部分入射辐照度，再根据物体表面的BRDF函数，进行积分计算，得到物体表面的颜色，并最终反映到2D屏幕上即可。或者更直接的认为实时PBR中光源就是一组离散的RGB采样值即可，也就是一堆的Sample操作，当然对于非点光源，尤其是复杂的HDR环境映射来说，Sample都是个比较昂贵的操作，一般都会对光源纹理做预采样及Mipmap处理。而非实时PBR中直接光源就需要根据波长、强度比例等计算辐射度，或者辐射密度等，作为进一步计算时其它场景物体表面的入射辐照度（见前面介绍的光源波长积分）。

  一般的HDR环境映射纹理示例图如下（这里只是给大家个感性认识而已，真正的HDR图在一般的显示器上是没法直接显示的）：

  最终这里讨论的关于光源的计算，其实就是通常所说的直接光照和间接光照，分别对应来源于直接光源光照的计算和来自二次或高次反射后的光源也就是间接光源的计算。

6.3、计算量及计算复杂度评估

  刚才的介绍中，我们已经计算过了完全漫反射的BRDF，并且揭示了漫反射纹理的含义，这对于实时PBR和非实时PBR来说都是成立的。接下去就需要根据出射向量计算反射辐照度了，或者说要开始解算BRDF，并且开始进行复杂的积分计算了。

  首先我们来回顾一下刚才推导出的反射方程：

L

o

(

p

⃗

,

ω

o

⃗

)

=

∫

Ω

f

r

(

p

⃗

,

ω

i

⃗

,

ω

o

⃗

)

L

i

(

p

⃗

,

ω

i

⃗

)

n

⃗

⋅

ω

i

⃗

d

ω

i

⃗

式

中

使

用

 

n

⃗

⋅

ω

i

⃗

 

代

替

了

原

来

的

cos

⁡

θ

，

这

也

暗

示

式

中

使

用

的

 

n

⃗

、

ω

i

⃗

 

是

单

位

向

量

\\mathrm{L}_{o}(\\vec{p},\\vec{\\omega_{o}}) = \\mathop{\\int}_{\\Omega} {f}_{r}( \\vec{p} , \\vec{\\omega_i} , \\vec{\\omega_o}) \\mathrm{L}_{i} (\\vec{p},\\vec{\\omega_i}) \\vec{n} \\cdot \\vec{\\omega_i} d\\vec{\\omega_i} \\\\[2ex] 式中使用 \\ \\vec{n} \\cdot \\vec{\\omega_i} \\ 代替了原来的 \\cos \\theta，这也暗示式中使用的 \\ \\vec{n} 、\\vec{\\omega_i} \\ 是单位向量

Lo​(p

​,ωo​

​)=∫Ω​fr​(p

​,ωi​

​,ωo​

​)Li​(p

​,ωi​

​)n

⋅ωi​

​dωi​

​式中使用 n

⋅ωi​

​ 代替了原来的cosθ，这也暗示式中使用的 n

、ωi​

​ 是单位向量
  当然这个式子是对于非自发光体反射光的方程，那么对于自发光体来说，还需要添加一个发光体的出射辐照度函数

L

e

(

p

⃗

,

ω

o

)

L_e(\\vec{p},\\omega_o)

Le​(p

​,ωo​)，整理如下：

L

o

(

p

⃗

,

ω

o

⃗

)

=

L

e

(

p

⃗

,

ω

o

)

+

∫

Ω

f

r

(

p

⃗

,

ω

i

⃗

,

ω

o

⃗

)

L

i

(

p

⃗

,

ω

i

⃗

)

n

⃗

⋅

ω

i

⃗

d

ω

i

⃗

\\mathrm{L}_{o}(\\vec{p},\\vec{\\omega_{o}}) = L_e(\\vec{p},\\omega_o) + \\mathop{\\int}_{\\Omega} {f}_{r}( \\vec{p} , \\vec{\\omega_i} , \\vec{\\omega_o}) \\mathrm{L}_{i} (\\vec{p},\\vec{\\omega_i}) \\vec{n} \\cdot \\vec{\\omega_i} d\\vec{\\omega_i}

Lo​(p

​,ωo​

​)=Le​(p

​,ωo​)+∫Ω​fr​(p

​,ωi​

​,ωo​

​)Li​(p

​,ωi​

​)n

⋅ωi​

​dωi​

​
  之所以使用相加，是因为刚才讨论过的关于BRDF整个是线性函数的原因，对于实时PBR来说自发光只考虑光源的一个RGB值即可，更复杂一点就是从另一个HDR光源纹理上Sample，然后再积分得到一个值，当然这时候这个物体往往就变成了光源，会直接被别的被照射物体使用。我们一般很少再去计算光源的反射光，也就是忽略第二项积分。当物体不会自发光时，只需要忽略自发光项即可。

  接着来思考如何计算后面这个积分项（或者叫做反射项）：

  首先，需要知道物体表面的BRDF函数

f

r

(

p

⃗

,

ω

i

⃗

,

ω

o

⃗

)

{f}_{r}( \\vec{p} , \\vec{\\omega_i} , \\vec{\\omega_o})

fr​(p

​,ωi​

​,ωo​

​)，并且需要考虑它同时是点p、入射光、出射方向（其实就是通常说的视方向）的函数，即需要找到这个函数的表达式。通常它是一个较复杂的函数，因为真实物体表面的反射过程是很复杂的，不但每个物体表面的实际BRDF都不一样，并且可能每个临近的点之间反射的效果都不一样，可以想象一下人体或动物的皮肤、粗糙物体表面、或者波澜壮阔的海面等，它们的BRDF该如何统一且简单的表达？

  其次，入射辐照度函数

L

i

(

p

⃗

,

ω

i

⃗

)

\\mathrm{L}_{i} (\\vec{p},\\vec{\\omega_i})

Li​(p

​,ωi​

​) ，根据前面的讲解，这个函数会有两大类情况，一类情况是来自于直接光源的直接光照，另一类是来自其它物体反射的光线也就是间接光照。同时这两大类情况都相对较复杂，当然幸运的是，无论间接光照怎么样递归去计算，最终它就是来自于某个光源或多个光源的辐射。所以可以先仅考虑直接光照的辐射的计算。接着根据刚才介绍的RGB颜色的知识，可以知道在实时PBR中，这里可以直接用一个RGB值（点光源）或者是一副HDR环境映射根据

p

⃗

,

ω

i

⃗

\\vec{p}, \\vec{\\omega_i}

p

​,ωi​

​ 采样一组HDR的RGB值得到（又碰到采样！），并且考虑到这两个向量间也有关系，所以这个函数最终计算上并不复杂，实质上在代码中往往使用sample操作就可以搞定。当然对于非实时PBR来说，这个函数将依然是一个积分方程，可以看前面的辐照度的积分方程，其计算依然是比较复杂的；

  再次，式中

n

⃗

⋅

ω

i

⃗

d

ω

i

⃗

\\vec{n} \\cdot \\vec{\\omega_i} d\\vec{\\omega_i}

n

⋅ωi​

​dωi​

​ 这一项是最简单和直接的，其中法线可以直接来自于法线贴图（还是采样！），

ω

i

\\omega_i

ωi​ 可以直接根据光源点和点p进行计算，当然需要归一化，而最后的

d

ω

i

d\\omega_i

dωi​ （含义是立体角微分元，前面有介绍）就直接用

ω

i

\\omega_i

ωi​ 向量代替即可；

  又次，积分计算一般就是根据p点正半球的立体角微元（向量）进行数值积分计算即可（直接计算时，一般使用球面坐标系），通常就是“累加和”运算（通常需要千次左右的循环，循环中可能嵌套了若干个Sample操作），但为了精度的时候其计算量还是比较大的，也既精度往往需要靠增加循环上限次数来达到，当然实际中这个积分计算往往采用“蒙特卡洛积分”方法（3D数学系列之——从“蒙的挺准”到“蒙的真准”解密蒙特卡洛积分！）。

  最后，假设上面的积分运算我们已经做完了，那么得到的其实只是一个点上某个特定方向（一般也就是视点到点p的方向）

ω

o

\\omega_o

ωo​ 上的一个RGB值而已，也就是点亮了像素上的一个点而已（这里先考虑最简单的情形）。如果要渲染出整个2D屏幕上所有的点（也就是为每个像素着色），那么其计算量等同于就是屏幕像素个数，对于4k渲染来说这个数是

4096

×

2160

=

8847360

4096 \\times 2160 = 8847360

4096×2160=8847360次。再假设每个像素点需要计算的反射辐照度积分方程，假设平均每个积分运算需要1024次运算（不明白，请去了解下数值积分先），那么最终计算次数就变成

4096

×

2160

=

8847360

×

1024

=

9

,

059

,

696

,

640

4096 \\times 2160 = 8847360 \\times 1024 = 9,059,696,640

4096×2160=8847360×1024=9,059,696,640 次运算，大约=8G次运算，若GPU的频率为3G（未来应该是这个级别），那么其周期大约是0.31纳秒，又假设该GPU有10240个计算单元，那么完成这么多计算大约需要：

9

,

059

,

696

,

640

÷

10240

÷

3.1

×

1

0

−

10

∼

0.285

毫

秒

9,059,696,640 \\div 10240 \\div 3.1 \\times 10^{-10} \\sim 0.285毫秒

9,059,696,640÷10240÷3.1×10−10∼0.285毫秒 当然这个只是最简单场景“一摄像机一屏幕一物体一光源”并且配置了超级显卡的情况下的理论值（换算一下CPU上完成这个计算大概要多久？），而这还没有考虑BRDF函数的复杂度，n个慢速 Sample操作，以及更大积分计算量等的影响，如果按照我们之前的讨论再将间接光照考虑进去，以及场景中有多个光源，比如夜晚的某个车水马龙灯红酒绿的街头，或浩瀚星辰照射下的海面，或者充满了发光生物的大海等等，可以想象下什么样的显卡才能抗住这样的计算量下还要至少达到60帧速率的要求？

  综合上面的分析，可以深刻的感受到PBR计算的过程其计算复杂度和计算量都是一个空前的挑战，如果非要实时的PBR，并且至少达到60帧以上并且能够做到场景自由的要求，并考虑到目前的以及未来一定时期内GPU的计算能力来说，除了对光源模型的简化外，我们还需要进一步做更多简化。幸运的是至少有两个突破口，一个就是简化BRDF函数，另一个就是需要简化积分计算。首先就让我们来看看如何简化或者说通俗化表达BRDF函数。（关于积分的简化放在后续教程中。）

6.4、迪士尼原则

  在现实世界中，要直接得到物体表面的BRDF函数解析式是极不容易的，甚至是不可能的，即使得到表达式也是过于复杂或者是令人费解的，还有可能就是每种材质表面的BRDF都是不一样的，而获取这些BRDF往往还需要耗费巨大的人力物力，并且需要大量专业且昂贵的设备，比如高级的光谱仪之类。网上也有很多直接测量得到的特定材质表面的BRDF函数的数值表，但数据库规模和复杂度也不小，同时也没什么简单的规律可循，并且这些材质还只是真实环境中材质的一小部分，还不足以用来表达充满多种复杂物体的场景。总之这些即不利于计算程序的编写，又不利于实际计算，而且也不利于美工去表达物体表面的材质特性，最终就导致如果要简单的达到PBR的电影级画质渲染，BRDF函数就成了第一个拦路虎。

  当然对于聪明的程序员来说这似乎不是太复杂的问题，也许聪明的你已经想到了，假设找到了一个“标准光源”去照射某个物体表面，然后测量其出射辐照度，简单的暴力反算（大致就是BRDF定义中的除法）出每个点的BRDF参数形成一个纹理不就行了？那么换个角度思考这个问题，这个BRDF是不是对所有特性的光源都是“对”的数值？怎么理解这些数值的含义？同时美工又怎么去调整这些值从而控制物体表面的视觉效果呢？所以纹理不是万能的。（当然这种方法也不是不可行，有些算法中确实这样干的，但不是通过直接测量，后续的教程中，我会逐步介绍。）但即使这个方法可行，想象一下为了做一个魔法游戏，场景中不但有大量现实物品需要去测量其BRDF，还有大量的魔法物体即现实中不存在的物体其表面的BRDF又怎么办？

  基于这样的原因，这曾一度阻挡不论是非实时PBR以及实时PBR的应用与普及。

  时间到了2012年，迪士尼动画工作室的Brent Burley于SIGGRAPH 2012上进行了著名的《Physically-based shading at Disney》，正式提出了迪士尼原则的BRDF（Disney Principled BRDF），由于其高度的通用性，将材质复杂的物理属性，用非常直观的少量变量表达了出来（如金属度metallic和粗糙度roughness），在电影业界和游戏业界引起了不小的轰动。从此，基于物理的渲染正式进入大众的视野。这也使得实时PBR成为可能。

  具体的迪士尼提出，着色模型应该是艺术导向（Art Directable）的，而不一定要是完全物理正确(Physically Correct) 的，并且对微平面BRDF的各项都进行了严谨的调查，并提出了清晰明确而简单的函数表达式。所谓艺术导向，就是说，美工有了直观容易表达的参数来“定义”BRDF，而程序也可以针对参数方便的生成BRDF，最终带来的不只是工作量的大大简化（现在已经有很多PBR参数纹理生成工具，可以了解下），而且在计算上也相对容易了很多。而不一定完全物理正确，就是说，实际使用的BRDF函数，仅是大多数真实BRDF的一种近似模拟，这其实是一种在现实中经常用到的方法，比如用线性回归法得到一组点组成的近似直线表达式，多项式捏合法用多项式去拟合一条复杂的曲线图像或一组复杂的函数数据 等等，而且这种近似捏合也使得原本复杂的函数变的简单了很多。

  基于上面这样的目标和认识，迪士尼提出了被命名为迪士尼原则的BRDF（Disney Principled BRDF）核心原则：

a、应使用直观的参数，而不是物理类的晦涩参数（美工、特效师、程序等等都能明确知道这个参数的含义）。
b、参数应尽可能少（想象一下因为参数太多，美工小姐姐为了调出一个特效，而不断加班赶进度以至于秃顶的后果）。
c、参数在其合理范围内应该为0到1（可以进一步理解为百分比，这样大家讨论的时候，就会说你把xx参数调整到50%，而把另一个参数xx调整到20%试试看）。
d、允许参数在有意义时超出正常的合理范围（这允许特效师想标新立异时，可以因为使用了某个200%的参数从而得到一个极具视觉冲击的效果）。
e、所有参数组合应尽可能健壮和合理（这些参数要尽可能多的适用各种材质而不失效，并且能够在各种光照环境下表现的都高度一致，并且与人类真实视觉感受基本一致，本质上也就是保证能量守恒性和线性）。

  最终在这些原则的指导下，首先诞生了现在称之为“金属工作流”的BRDF。即使用所谓金属度的参数在金属与非金属材质间线性插值，从而可以统一的表达金属与非金属的渲染。最最重要的就是，迪士尼原则的BRDF几乎用一个统一的函数描述了所有非透明物体表面的反光特性，这为程序的编写、美工建模都带来了巨大的好处。而同时如我们之前所说，场景中大多数物体几乎都是非透明物体。

  当然迪士尼之所以能够提出迪士尼原则以及我们马上要看到的迪士尼原则的BRDF的表达式，是基于他们观察了很多很多实际材质的BRDF的表现，并且基于一些实际测量的BRDF数据，进行了大量分析后得出的总结。迪士尼原则BRDF最神奇的地方就在于仅用几个并不复杂的参数就可以表达几乎所有非透明物体表面材质的各种反光特性！

6.5、基本渲染方程

  根据迪士尼原则，现代实时PBR渲染中，比较通用的一种反射BRDF是被称为 Cook-Torrance BRDF 模型。

  首先 Cook-Torrance 模型中将BRDF按照之前的分析，自然的分为了漫反射部分和镜面反射两个部分：

f

r

=

κ

d

f

l

a

m

b

e

r

t

+

κ

s

f

c

o

o

k

−

t

o

r

r

a

n

c

e

其

中

：

 

(

κ

d

+

κ

s

)

⩽

1

{f}_{r} = {\\kappa}_d {f}_{lambert} + \\kappa_s {f}_{cook-torrance} \\\\[2ex] 其中： \\ ( {\\kappa}_d + \\kappa_s ) \\leqslant 1

fr​=κd​flambert​+κs​fcook−torrance​其中： (κd​+κs​)⩽1
  式中

κ

d

、

κ

s

{\\kappa}_d 、 \\kappa_s

κd​、κs​ 分别理解为漫反射部分的百分比和镜面反射部分的百分比，二者之和不能大于1，以保证能量守恒规则被严格遵守。在本章示例代码中，这个规则主要体现在下面这段Shader代码中：

  特别注意代码中被红框标记的部分，可以看出kD系数被乘以了一个1.0减去金属度参数的系数，显然如果金属度接近于1.0f的时候，那么kD因子几乎就接近于0，这是为什么呢？

  其实这是因为，在 Cook-Torrance BRDF 模型中，最主要的参数就是这个金属度参数，它表示一个材质表面是不是完全金属成分的一个参数，而经过迪士尼大量的分析后发现，其实在完全金属表面，反射光中是不包含漫反射成分的，实际中，当光照射到金属的时候，除了被反射的光线外，其它光基本都是被金属内部吸收了，想想光电效应试验，当光子频率（波长）达到一定阈值后，金属表面的电子直接就被“撞”了出来，而低于这个阈值时其实还是被电子吸收了，只是其能量不足以使电子飞出金属表面而已，这是金属材质特有的特性。

  而在传统的光照模型中因为基本没有考虑这个因素，无论什么材质表面都会有高光部分（镜面反射）+漫反射光部分+环境光部分，最终导致即使是真正的金属表面因为错误了加入了漫反射部分，所以最终造成的结果就是金属表面看上去有浓浓的“塑料”味道。最终在在 Cook-Torrance BRDF 模型中就引入了这个金属度参数，以区分金属材质和非金属材质（有些资料中叫做金属与绝缘体，有些叫导电介质或电介质等，表达的都是这里的意思），以及介于二者之间的材质。

  本章示例运行后，当把金属度参数调整到接近于1的时候，就会发现材质表面只有几个光点，而其它部分几乎都是黑色的原因就是因为此时几乎没有了漫反射光，而只有镜面反射形成的高光所导致的（其实在PBR中再讲镜面反射有点不太合适，这里只是为了让大家明白背后的原理，真正的反射出的光线总是一个“喇叭形”出射光，结合前面的知识想想为什么？）。

  从前面的式子中可以看出，BRDF函数被线性的拆分了，这与我们之前讲的BRDF的线性特征是一致的，所以这样的拆分是合理有效的。

  其中

f

l

a

m

b

e

r

t

{f}_{lambert}

flambert​ 就是我们前面推导的Lambertian漫反射BRDF，所以直接引用：

f

l

a

m

b

e

r

t

=

c

π

c

表

示

表

面

漫

反

射

颜

色

（

回

忆

下

之

前

的

知

识

）

{f}_{lambert} = \\cfrac{c}{\\pi} \\\\[2ex] c 表示表面漫反射颜色（回忆下之前的知识）

flambert​=πc​c表示表面漫反射颜色（回忆下之前的知识）
  当然这是本章示例中针对点光源时采取的方式，在多光源，甚至HDR环境光映射中使用的时候，必须要退回漫反射积分方程中去使用，要对所有的入射辐照进行一个积分，这个之后的教程中会继续详细讲。

  接着 Cook-Torrance 模型中的镜面反射BRDF函数就要稍微复杂一些，具体定义如下：

f

c

o

o

k

−

t

o

r

r

a

n

c

e

=

D

⋅

F

⋅

G

4

(

ω

o

⃗

⋅

n

⃗

)

(

ω

i

⃗

⋅

n

⃗

)

{f}_{cook-torrance} = \\cfrac{D \\cdot F \\cdot G}{4 ( \\vec{\\omega_o} \\cdot \\vec{n} ) (\\vec{\\omega_i} \\cdot \\vec{n} ) }

fcook−torrance​=4(ωo​

​⋅n

)(ωi​

​⋅n

)D⋅F⋅G​
  至于这个式子怎么来的，目前我们的目标是怎么用它来写程序进行渲染，至于推导可以不用过多关注（其实我也没太搞明白怎么来的，但大致的说法就是迪士尼的工程师根据一堆BRDF数据使用“瞪眼法”得到的:-）。同时因为这里也是一个遵循迪士尼原则的艺术化的近似，并不是纯粹物理真实的公式，也就是说它是个被“发明”的公式，也就不需要过分纠结怎么来的了（目前不要过多关注细节，先注重实现，再逐步深入）。

  字母 D、F、G 分别代表描述物体表面反射特征一个方面的函数。

6.5.1、D 法线分布函数(Normal Distribution Function)，

  这个函数根据给定的粗糙度参数来计算微表面模型下，微表面中各个点的法线与平均值之间的偏差。

  其实从这个函数的名字以及它要表达的意思，基本可以理解其含义，也就是说在一个“粗糙”的微表面上（微表面仍然是表面！），其各点法线方向与平均方向是偏差很大很远的，这直接影响镜面反射光的方向并不是朝一个理想的整体方向反射，而有可能是随机的被反射了，从最终视觉效果来说，物体的表面上“高光”的效果就会很差，看上去“灰蒙蒙”的很粗糙。这里要注意我们说的表面就是微表面，但即就是微表面对于“光子”来说，他们也几乎是个“无穷大”的存在了，所以微表面上的“光滑”程度直接影响到每个“光子”反射的路径。这个可以直接想象将几乎“无穷多”个“光子”都按照传统的“镜面”反射模型微缩到一个各点法线不尽相同的微平面上后的效果。

  具体的这个函数被定义为如下形式：

D

=

N

D

F

G

G

X

T

R

(

n

⃗

,

h

⃗

,

α

)

=

α

2

π

(

(

n

⃗

⋅

h

⃗

)

2

(

α

2

−

1

)

+

1

)

2

N

D

F

:

N

o

r

m

a

l

 

d

i

s

t

r

i

b

u

t

i

o

n

 

f

u

n

c

t

i

o

n

T

R

:

T

r

o

w

b

r

i

d

g

e

−

R

e

i

t

z

D = NDF_{GGXTR}(\\vec{n},\\vec{h},\\alpha) = \\frac{ \\alpha^2 }{\\pi (( \\vec{n} \\cdot \\vec{h} )^2(\\alpha^2 – 1) + 1) ^ 2} \\\\[2ex] NDF:Normal \\ distribution \\ function \\\\[2ex] TR:Trowbridge-Reitz

D=NDFGGXTR​(n

,h

,α)=π((n

⋅h

)2(α2−1)+1)2α2​NDF:Normal distribution functionTR:Trowbridge−Reitz
  这里的D函数就是 Epic 在 UE4 中使用的版本，具体称之为 Trowbridge-Reitz GGX（来自于2007年著名的图形学会议EGSR（Eurographics Symposium on Rendering），而 GGX 也正是首次在这篇文章中提出，GGX具体含义不可考）。

  式中

α

\\alpha

α 即表面粗糙度系数roughness，取值在 0.0f – 1.0f 之间 ，

n

⃗

\\vec{n}

n

是平面的法向量，这里可以理解为是这个平面的“平均法向量”，

h

⃗

\\vec{h}

h

就是入射光线与反射光线的中间向量，这个也是传统光照模型改良后经常用到的一个向量，需要注意的是当有多个光源，或者说需要对所有入射光线进行积分时，那么

h

⃗

\\vec{h}

h

就需要对每个入射光线进行积分计算，因此要将

h

⃗

\\vec{h}

h

理解为是入射光线

ω

i

⃗

\\vec{\\omega_i}

ωi​

​ 和出射光线

ω

o

⃗

\\vec{\\omega_o}

ωo​

​ 的函数。

  通常在程序中

ω

o

⃗

\\vec{\\omega_o}

ωo​

​ 就是“视向量”，在光追渲染中就从平面像素点到物体表面的光照点，在光栅化渲染中就从虚拟摄像机到物体表面像素点。

  在本章代码中，D-TRGGX的 Shader 代码实现如下：

float Distribution_GGX( float3 N, float3 H, float fRoughness )
{
    float a = fRoughness * fRoughness;
    float a2 = a * a;
    float NdotH = max( dot( N, H ), 0.0 );
    float NdotH2 = NdotH * NdotH;

    float num = a2;
    float denom = ( NdotH2 * ( a2 - 1.0 ) + 1.0 );
    denom = PI * denom * denom;

    return num / denom;
}

  这段代码很容易懂，是直接翻译自公式，就不过多赘述了。代码中fRoughness变量即为表面粗糙度系数

α

\\alpha

α 。

6.5.2 F 菲涅尔方程

  菲涅耳反射系数作为 Cook-Torrance BRDF 模型的一个系数，在 PBR 中也起着至关重要的作用。法国物理学家奥古斯丁 · 让 · 菲涅耳观察到的菲涅耳效应指出，从一个表面反射的光的数量取决于它被观察的视角。想象一池水,如果你垂直于水面向下看，你可以看到底部。以这种方式观察水面将在零度或正入射，正入射是表面的法向。如果你以掠入射的角度看水池，即几乎平行于水面，你会看到水面上的镜面反射变得更强烈，此时可能根本无法看到水面以下。

  在PBR中，这是由PBR着色器模拟物体表面物理特征的另一个方面。当以掠入射（与入射光垂直的方向）的方式观察表面时，所有平滑的表面在90度入射角时几乎100%成为反射器。

  对于粗糙表面，反射率将变得越来越高光，但不会接近100%的高光反射。这里最重要的因素是每个微平面的法线与光线之间的角度，而不是宏观表面的法线与光线之间的角度。因为光线分散在不同的方向，反射看起来更柔和或更暗淡。宏观层面上发生的情况与你在全体微观层面上观察到的所有菲涅耳效应的平均值有些相似。

  最终菲涅尔方程描述的是被反射的光线对比光线被折射的部分所占的比率，这个比率会随着我们观察的角度不同而不同。当光线碰撞到一个表面的时候，菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比。利用这个反射比率和能量守恒原则，我们可以直接得出光线被折射的部分以及光线剩余的能量。

  本身菲涅尔方程是非常复杂的，而 Cook-Torrance BRDF 模型中用如下的 Fresnel-Schlick 近似法求得近似解：

F

=

F

S

c

h

l

i

c

k

(

h

⃗

,

v

⃗

,

F

0

)

=

F

0

+

(

1

−

F

0

)

(

1

−

(

h

⃗

⋅

v

⃗

)

)

5

F = F_{Schlick}(\\vec{h},\\vec{v},F_0) = F_0 + ( 1 – F_0 )(1 – (\\vec{h} \\cdot \\vec{v}))^5

F=FSchlick​(h

,v

,F0​)=F0​+(1−F0​)(1−(h

⋅v

))5
  其中

F

0

F_0

F0​ 称为0度时菲涅耳反射率，它是指当光线直射或垂直(以0度角)照射到表面时，一定比例的光线形成镜面反射。使用曲面的折射率，可以得出反射部分的能量。这被称为

F

0

F_0

F0​ (菲涅耳零点)。折射到表面的光量比例为

1

−

F

0

1 – F_0

1−F0​。

  大多数普通非金属的

F

0

F_0

F0​ 范围为 0.02- 0.05 (线性值)。对于金属，

F

0

F_0

F0​ 范围为 0.5- 1.0 。

  一般物体表面的

F

0

F_0

F0​ 参数的值，对于非金属(介质/绝缘体)来说就使用一个灰度值即可（一个通道），而对于金属(导体)则使用RGB值（三个通道）。对于PBR，从反射率的艺术解释可以得出，对于普通光滑的非金属表面，

F

0

F_0

F0​ 的反射度在2%到5%之间，在掠入射角度下为100%。

  一些常见物质表面的

F

0

F_0

F0​ 参数如下表所示：

材料	F 0 F_0 F0​ (线性)	F 0 F_0 F0​ (sRGB)
水	(0.02, 0.02, 0.02)	(0.15, 0.15, 0.15)
塑料/玻璃（低）	(0.03, 0.03, 0.03)	(0.21, 0.21, 0.21)
塑料（高）	(0.05, 0.05, 0.05)	(0.24, 0.24, 0.24)
玻璃（高）/红宝石	(0.08, 0.08, 0.08)	(0.31, 0.31, 0.31)
钻石	(0.17, 0.17, 0.17)	(0.45, 0.45, 0.45)
铁	(0.56, 0.57, 0.58)	(0.77, 0.78, 0.78)
铜	(0.95, 0.64, 0.54)	(0.98, 0.82, 0.76)
金	(1.00, 0.71, 0.29)	(1.00, 0.86, 0.57)
铝	(0.91, 0.92, 0.92)	(0.96, 0.96, 0.97)
银	(0.95, 0.93, 0.88)	(0.98, 0.97, 0.95)

  从理论上来说，一个物体表面要么是金属要么不是金属，不能两者皆是。但是，大多数的渲染管线都允许在0.0至1.0之间线性的调配金属度。这主要是由于材质纹理精度不足以描述一个拥有诸如细沙/沙状粒子/刮痕的金属表面。通过对这些小的类非金属粒子/刮痕调整金属度值，我们可以获得非常好看的视觉效果。这样就需要通过金属度参数微调物体表面的的

F

0

F_0

F0​ 值，我们可以对两种类型的表面使用相同的 Fresnel-Schlick 近似，但是如果是金属表面的话就需要使用基础漫反射颜色。我们一般是按下面这个样子来实现的（就是使用金属度参数在非金属

F

0

F_0

F0​ 值与金属漫反射颜色也就是金属的

F

0

F_0

F0​ 参数之间根据金属度参数插值 ）：

// PBR material parameters
cbuffer ST_CB_PBR_MATERIAL : register( b3 )
{
    float3   g_v3Albedo;      // 反射率
    float    g_fMetallic;     // 金属度
    float    g_fRoughness;    // 粗糙度
    float    g_fAO;           // 环境光遮蔽
};

......

float3 F0 = float3( 0.04f, 0.04f, 0.04f );
// Gamma矫正颜色(这个后续的教程再讲，也可以不这样做，而直接使用前表中线性F0值即可)
float3 v3Albedo = pow( g_v3Albedo, 2.2f );
F0 = lerp( F0, v3Albedo, g_fMetallic );

......

float3 Fresnel_Schlick( float cosTheta, float3 F0 )
{// 直接根据近似公式编码菲涅尔系数函数
	return F0 + ( 1.0 - F0 ) * pow( 1.0 - cosTheta, 5.0 );
}

  上述函数的实现就是公式直接翻译为代码，没什么难理解的，需要注意的是，作为Cook-Torrance BRDF模型中的镜面反射项中的一个函数，这是唯一的与材质表面颜色发生关系的项，也是唯一引用到金属度参数的项，但这一项直接影响了最终镜面反射项的颜色，而其它两项只是影响到最终光子数量的多少，而间接影响到出射光的明暗程度或者说间接的影响了能量，而这项直接改变了光波长，也就是直接改变了颜色和能量，所以这是较重要的一项，而也因此整个模型几乎就可以用来表达从金属到非金属所有材质表面的镜面反射特性，从而使得整个模型又被称之为“金属工作流”。如果你深入的研究过这个函数你还会发现这个函数是这三个函数中最接近物理真实的一个函数，因为它就是物理真实菲涅尔反射特性的最接近的近似函数。而其它两个函数则主要基于“概率”近似模拟。

6.5.2、G 几何函数 （Geometry Function）

  几何函数从统计学上近似的求得了微平面间相互遮蔽的比率，这种相互遮蔽会损耗光线的能量。实际上这些表面相互遮蔽的部分通常可能就是凸出的毛刺或者是凹陷的小坑，而这些被遮挡的光线与被吸收的不太相同，而在其它两个函数中也没有考虑这个情况，所以需要单独的函数来对这种微观上遮挡现象进行计算。

  通常这些被遮挡的光线有可能就像是被吸收了一样，所以总的出射能量会因为这种情况，而减少。在这个函数的具体建模上，一样需要表面粗糙度作为参数，这是显而易见的，因为越是粗糙的表面，互相遮挡的几率就越高。最终几何函数得到的值是一个范围在0.0f-1.0f之间的数，0.0f就表示该表面粗糙到所有光线都被内部遮挡了，最终就看上去黑乎乎的一团，而1.0f则表示该表面非常光滑，没有什么遮挡，光线就按照正常的反射路径射出。

  在Cook-Torrance BRDF模型中，常用的几何函数称之为Schlick-GGX：

G

=

G

S

c

h

l

i

c

k

G

G

X

(

n

⃗

,

v

⃗

,

κ

)

=

n

⃗

⋅

v

⃗

(

n

⃗

⋅

v

⃗

)

(

1

−

κ

)

+

κ

κ

d

i

r

e

c

t

=

(

α

+

1

)

2

8

κ

I

B

L

=

α

2

2

G

(

n

⃗

,

v

⃗

,

l

⃗

,

κ

)

=

G

s

u

b

(

n

⃗

,

v

⃗

,

κ

)

G

s

u

b

(

n

⃗

,

l

⃗

,

κ

)

G = G_{SchlickGGX}(\\vec{n},\\vec{v},\\kappa) = \\frac{\\vec{n} \\cdot \\vec{v}}{(\\vec{n} \\cdot \\vec{v})(1-\\kappa) + \\kappa } \\\\[2ex] \\kappa_{direct} = \\frac{(\\alpha + 1)^2}{8} \\\\[2ex] \\kappa_{IBL} = \\frac{\\alpha^2}{2} \\\\[2ex] G(\\vec{n},\\vec{v},\\vec{l},\\kappa) = G_{sub}(\\vec{n},\\vec{v},\\kappa) G_{sub}(\\vec{n},\\vec{l},\\kappa)

G=GSchlickGGX​(n

,v

,κ)=(n

⋅v

)(1−κ)+κn

⋅v

​κdirect​=8(α+1)2​κIBL​=2α2​G(n

,v

,l

,κ)=Gsub​(n

,v

,κ)Gsub​(n

,l

,κ)
  式中

α

\\alpha

α 就是在法线分布函数中用到的粗糙度因子，

κ

d

i

r

e

c

t

\\kappa_{direct}

κdirect​ 是在点光源情况下使用的换算系数，也是本章示例中使用的系数，而

κ

I

B

L

\\kappa_{IBL}

κIBL​ 则是在使用HDR环境映射光照情况下使用的换算系数，这个我们后续的教程中会进一步介绍。最后几何函数需要在入射光和出射光两个方向分别计算遮挡的情况，最后合成最终的遮挡情况，因为微表面上布满突刺或凹陷时，入射光和出射光都有可能被遮挡，所以这里需要从两个方向来模拟计算，并且因为最终BRDF要求对出射和入射方向都一致，所以两个方向的计算是一样的这就保证了BRDF的“双向性”。

  那么在本章Shader代码中，具体的几何函数代码实现如下：

float Geometry_Schlick_GGX( float NdotV, float fRoughness )
{
    float r = ( fRoughness + 1.0 );
    float k = ( r * r ) / 8.0;

    float num = NdotV;
    float denom = NdotV * ( 1.0 - k ) + k;

    return num / denom;
}

float Geometry_Smith( float3 N, float3 V, float3 L, float fRoughness )
{
    float NdotV = max( dot( N, V ), 0.0 );
    float NdotL = max( dot( N, L ), 0.0 );
    float ggx2 = Geometry_Schlick_GGX( NdotV, fRoughness );
    float ggx1 = Geometry_Schlick_GGX( NdotL, fRoughness );

    return ggx1 * ggx2;
}

7、点光源条件下的Cook-Torrance BRDF模型PBR的完整实现

7.1、完整Pixel Shader

  本章示例中最后Pixel Shader的完整实现如下，代码重点参考了[OpenGl版PBR基础教程](https://learnopengl-cn.github.io/07 PBR/01 Theory/)：

static const float PI = 3.14159265359;

cbuffer MVPBuffer : register( b0 )
{
    float4x4 mxWorld;                   //世界矩阵，这里其实是Model->World的转换矩阵
    float4x4 mxView;                    //视矩阵
    float4x4 mxProjection;				//投影矩阵
    float4x4 mxViewProj;                //视矩阵*投影
    float4x4 mxMVP;                     //世界*视矩阵*投影
};

// Camera
cbuffer ST_CB_CAMERA: register( b1 )
{
    float4 g_v4CameraPos;
};

#define GRS_LIGHT_COUNT 8
// lights
cbuffer ST_CB_LIGHTS : register( b2 )
{
    float4 g_v4LightPos[GRS_LIGHT_COUNT];
    float4 g_v4LightClr[GRS_LIGHT_COUNT];
};

// PBR material parameters
cbuffer ST_CB_PBR_MATERIAL : register( b3 )
{
    float3   g_v3Albedo;        // 反射率
    float    g_fMetallic;           // 金属度
    float    g_fRoughness;      // 粗糙度
    float    g_fAO;                  // 环境光遮蔽
};

struct PSInput
{
    float4 g_v4PosWVP   : SV_POSITION;
    float4 g_v4PosWorld : POSITION;
    float4 g_v4Normal   : NORMAL;
    float2 g_v2UV       : TEXCOORD;
};

float3 Fresnel_Schlick( float cosTheta, float3 F0 )
{
	return F0 + ( 1.0 - F0 ) * pow( 1.0 - cosTheta, 5.0 );
}

float Distribution_GGX( float3 N, float3 H, float fRoughness )
{
    float a = fRoughness * fRoughness;
    float a2 = a * a;
    float NdotH = max( dot( N, H ), 0.0 );
    float NdotH2 = NdotH * NdotH;

    float num = a2;
    float denom = ( NdotH2 * ( a2 - 1.0 ) + 1.0 );
    denom = PI * denom * denom;

    return num / denom;
}

float Geometry_Schlick_GGX( float NdotV, float fRoughness )
{
    // 直接光照时 k = (fRoughness + 1)^2 / 8;
    // IBL 时 k = （fRoughness^2)/2;
    float r = ( fRoughness + 1.0 );
    float k = ( r * r ) / 8.0;

    float num = NdotV;
    float denom = NdotV * ( 1.0 - k ) + k;

    return num / denom;
}

float Geometry_Smith( float3 N, float3 V, float3 L, float fRoughness )
{
    float NdotV = max( dot( N, V ), 0.0 );
    float NdotL = max( dot( N, L ), 0.0 );
    float ggx2 = Geometry_Schlick_GGX( NdotV, fRoughness );
    float ggx1 = Geometry_Schlick_GGX( NdotL, fRoughness );

    return ggx1 * ggx2;
}

float4 PSMain( PSInput stPSInput ) : SV_TARGET
{
    // 使用插值生成的光滑法线
    float3 N = normalize( stPSInput.g_v4Normal.xyz );
    // 视向量
    float3 V = normalize( g_v4CameraPos.xyz - stPSInput.g_v4PosWorld.xyz );

    float3 F0 = float3( 0.04f, 0.04f, 0.04f );

    // Gamma矫正颜色
    float3 v3Albedo = pow( g_v3Albedo, 2.2f );
    
    F0 = lerp( F0, v3Albedo, g_fMetallic );

    // 出射辐射度
    float3 Lo = float3( 0.0f, 0.0f, 0.0f );

    // 粗糙度
    float fRoughness = g_fRoughness;

    for ( int i = 0; i < GRS_LIGHT_COUNT; ++i )
    {// 对每一个光源求解光照积分方程
        // 点光源的情况
        // 入射光向量
        float3 L = normalize( g_v4LightPos[i].xyz - stPSInput.g_v4PosWorld.xyz );
        // 中间向量（入射光与法线的角平分线）
        float3 H = normalize( V + L );
        float distance = length( g_v4LightPos[i].xyz - stPSInput.g_v4PosWorld.xyz );

        //float attenuation = 1.0 / ( distance * distance );
        // 已经Gamma矫正了，就不要二次反比衰减了，单次衰减就可以了
        float attenuation = 1.0 / distance ;
        
        float3 radiance = g_v4LightClr[i].xyz * attenuation;

        // Cook-Torrance光照模型 BRDF
        float NDF = Distribution_GGX( N, H, fRoughness );
        float G = Geometry_Smith( N, V, L, fRoughness );
        float3 F = Fresnel_Schlick( max( dot( H, V ), 0.0 ), F0 );

        float3 kS = F;
        float3 kD = float3( 1.0f,1.0f,1.0f ) - kS;
        kD *= 1.0 - g_fMetallic;

        float3 numerator = NDF * G * F;
        float denominator = 4.0 * max( dot( N, V ), 0.0 ) * max( dot( N, L ), 0.0 );
        float3 specular = numerator / max( denominator, 0.001 );

        // add to outgoing radiance Lo
        float NdotL = max( dot( N, L ), 0.0 );
        Lo += ( kD * v3Albedo / PI + specular ) * radiance * NdotL;
    }

    float fAO = g_fAO;
    // 环境光项
    float3 ambient = float3( 0.03f, 0.03f, 0.03f ) * v3Albedo * fAO;
    float3 color = ambient + Lo;

    color = color / ( color + float3( 1.0f,1.0f,1.0f ) );
    // Gamma 矫正
    color = pow( color, 1.0f / 2.2f );
    return float4( color, 1.0 );
}

7.2 关于最终Pixel Shader PSMain函数的一些补充说明

  Cook-Torrance BRDF模型的BRDF函数的主体实现部分在前面已经详细介绍过了，那么这里重点在解析下PSMain函数中的一些逻辑。

  第一、具体实现时对于点光源做了距离平方反比衰减处理，具体代码就是：

float distance = length( g_v4LightPos[i].xyz - stPSInput.g_v4PosWorld.xyz );
float attenuation = 1.0 / ( distance * distance );
float3 radiance = g_v4LightClr[i].xyz * attenuation;

  第二、最终计算出的BRDF函数值其实是个3D向量：

float3 numerator = NDF * G * F;
float denominator = 4.0 * max( dot( N, V ), 0.0 ) * max( dot( N, L ), 0.0 );
float3 specular = numerator / max( denominator, 0.001 );

  其中几个max主要是为了防止发生除0错误而特意加入的。

  第三、最终出射光需要针对每个光源进行累加：

float NdotL = max( dot( N, L ), 0.0 );
Lo += ( kD * v3Albedo / PI + specular ) * radiance * NdotL;

  注意上面实现中，严格遵照前面介绍的BRDF被拆分成两部分：镜面反射部分和漫反射部分。在这里进行了系数合成，然后统一作为系数函数，乘以入射光，最终累加作为反射光。这些都是从公式到代码的简单翻译。

  第四、最终像素着色中，考虑了环境光项，这与传统光照中使用的手法类似，根本原因就是因为我们之前说的忽略或简化了很多高次反射等光照因素后的一个折中方法：

    float fAO = g_fAO;
    // 环境光项
    float3 ambient = float3( 0.03f, 0.03f, 0.03f ) * v3Albedo * fAO;
    float3 color = ambient + Lo;

  其中 g_fAO 与在几何函数中的意义类似，都是环境遮挡因子，这里没有再过度的精细化处理，而是简单的使用了一个系数，模拟整个场景中物体间因为相互遮挡引起的光线能量损耗。

  第五、最终色彩做了从HDR颜色空间到sRGB空间再到普通RGB颜色空间的转换：

color = color / ( color + float3( 1.0f,1.0f,1.0f ) );
 // Gamma 矫正
color = pow( color, 1.0f / 2.2f );
return float4( color, 1.0 );

  其中，第一行代码转换的处理比较好理解，因为我们之前说过HDR的颜色值范围可能会大于1.0f，并且我们为了最终的效果，将点光源的RGB值都设置成了远大于1.0f的值，这都可能导致最终计算出来的颜色是超过1.0f范围的值，而这些值在一般的显示器是没法显示的，所以这里就做了类似向量“规范化”的处理。

8、总结

  至此非常感谢您的阅读！

  总算在几乎近一年的时间后，PBR的第一个教程算是完成了，也算了了自己的心愿。期间发生了很多事情，有些甚至改变了我的后半生，至此成文感慨万千，往后余生也只有继续奋斗，算不虚度年华。当然最近杂务缠身，之后程序什么时候更新，以及博客什么时候更新都是未知数，我只能保证说，只要我还活着我总会继续下去，只是请各位不要太着急，也非常感谢各位一直以来的支持与关注！

  不知不觉，又是一个中秋佳节，在这里提前预祝各位阖家欢乐！万事如意！

  关于本章代码的其余部分我就不再赘述了，相信对各位来说已经没什么难度了，为了避免复杂度，这一章的代码是基于单线程单显卡示例的，只是加入了全屏化的支持，方便各位细细的研究PBR渲染特性的一些直观特征。