在知识传播途中，向涉及到的相关著作权人谨致谢意！

克里格插值

【需要知道的东西】

1. 克里格插值的线性无偏是BLUE的（最好的方法）
2. 怎么才能BLUE呢？要达到它的假设
3. 它的假设是什么呢？空间平稳性假设
4. 插值之后有一个东西，方差变异函数

克里格插值的前提条件

【地统计学】以区域化变量为基础，借助变异函数，研究具有随机性和结构性、空间相关性和依赖性的自然现象的一门科学
【解释】地统计学的一种插值方法。不是说，克里格插值就是最好的，研究的对象如果满足了它的假设那才是最好的
【BLUE】数学里的概念BLUE，最佳线性无偏估计。克里格插值，只要满足假设，它就是BLUE的，是最佳线性无偏估计。如果不满足假设，那就不是最好的
【克里格插值的假设是什么？】空间平稳假设

1. 空间变异分析假设存在空间平稳性
   【均值平稳性】均值独立于位置，在样本之间是常数（均值和位置无关）
2. 随机过程不具有二阶平稳性
   【协方差的二阶平稳性和平方差函数的内秉性平稳】在相同方向和相同距离的任意两点之间的协方差相同。协方差与距离有关，而与位置无关 –> 我们就可以通过距离来反算一些东西

【平稳假设例子】

区域化变量

【区域化变量】地统计学方法假定在一定空间范围内性质的变异可以用一个连续随机但是空间上相关的随机域来模拟
【解释】注意不是性质本身，不是前面所谈到的空间相关。而是性质的变异，变异和相关是一个问题的两个方面

【模型】Z=m(x)+c(x)+e

1. Z：空间的属性值
2. m(x)：总的趋势 –> 是趋势面做的
3. c(x)：结构性成分，可以用模型来描述的 –> 克里格做的
4. e：随机的成分 –> 随机误差，不考虑的

【半方差函数】有一系列数(v1,v2,v3,v4,…)，给定一个h

1. 某个点的数v1 和 周围h内的所有的数 相减，然后平方，就求出了一个差异（即范围h内的方差，半方差=方差/2）
2. 这个数做完之后，做下一个数–>每个数都求出了变异量，反映的是这个数和周围数的差异。
3. 半方差函数即是 数的差异 随着 间隔h的变化。这个数的差异在空间上的变化

【区域化变量的特点】

1. 随机性：即局部不规则的随机性质，可以进行统计推断
2. 结构性：即存在某种空间自相关,可用某一数学函数来表示（能用函数来描述，有一定规则的，才有结构）

变异函数

【方差变异函数】度量Z的空间连续性的自然方法是比较间隔为h的两个点x，x＋h的值Z（x）和Z（x+h）
一个直接的度量关系是两个值间的绝对差

dZ（h）= Z（x）- Z（x＋h）

【解释】两个位置一减，看点与点之间的差异

【半变异函数】把方差变异的大小作为一个距离的函数，是地理学相近相似定理的定量化
【作用】用于定量描述空间变异和空间相关性，为克立金插值提供依据

典型的变异函数图

【图中的两个点】

1. 间隔为0时的点
2. 半变异函数趋近平稳时的拐点

【由这两个点产生四个相应的参数】

1. 块金值（Nugget）：理论上，当样点间的距离为0时，半变异函数值应为0；但由于存在观测误差和空间变异，使得两样点非常接近时，它们的半变异函数值不为0，即存在块金值
2. 基台值（Sill）：当样点间的距离h增大时，变异函数r(h)从初始的块金值达到一个相对稳定的常数时，该常数值称为基台值
3. 偏基台值（Partial Sill）：基台值与块金值的差值。
4. 变程（Range）：当变异函数的取值由初始的块金值达到基台值时，样点的间隔距离称为变程

【一些情况下四个参数的值】

变异函数的作用

这条曲线干嘛用呢？怎么看这条曲线呢？

1. 分析样点分布的格局类型
   
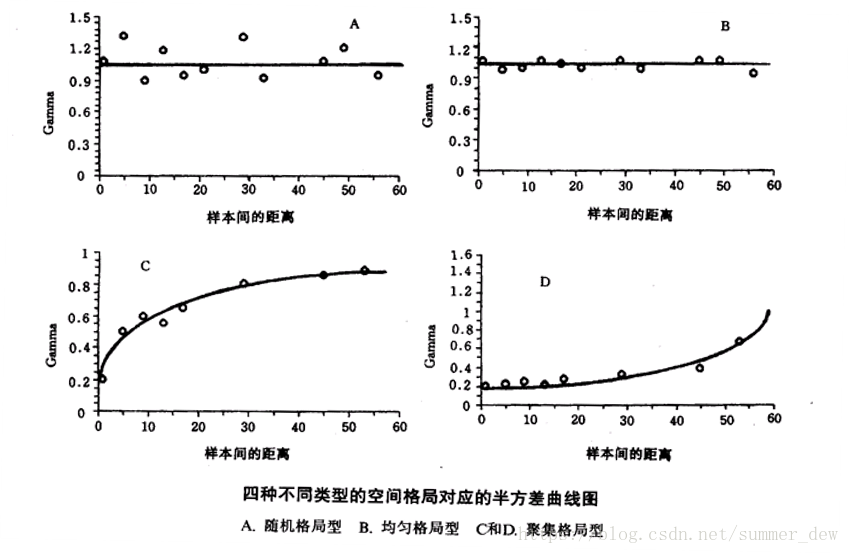
2. 空间克里金插值的基础

【半方差函数】也可以得出格局，和变异函数是两个角度，两种方法

进行插值

【做插值】有了方差变异函数就可以做插值了，就可以继续以下的工作
利用原始数据和半方差函数的结构性，对未采样点的区域化变量进行无偏最佳估值的一种方法。该方法的一个有用特点是能够计算出每个估值的误差大小(估值方差)，从而能知道估值的可靠性程度

【优点】会产生另外一个产品，插值的不确定性分析
【解释】其他插值方法不会告诉你，某一点插值的结果的不确定性。而克里格插值会告诉你，某个点插值所得的结果，它的变异性程度或者不确定性是10%，那么你就可以知道这是挺可信的
【为什么能够会产生了】前面有一个平稳性假设，如果你越满足了他的假设，满足了他数学的刻画，根据此就可以给出不确定分析

点克里格插值

1. 估计指定点的值。局部估值方法，每一估值都是由其邻近观测值加权平均计算而得
2. 用于研究指定点值及其可能的变异

块克里格插值

1. 对中心在X0的小区或块段进行估值
2. 绘制性质的等值线图，图中的等值线较平滑
3. 用于研究变异的区域格局

泛克里格

普通克立格方法(OK)要求数据是二阶平稳的或纯平稳的。如果数据在空间上存在明显的趋势，那么,应该使用泛克立格方法进行分析

【步骤】

1. 趋势分析
   分析数据中存在的空间上的变化趋势,获得拟合模型。这部分的分析内容与前面的趋势面分析相同
2. 残差的克立格分析
   与普通克立格分析相同，不同的是，使用的数据是原始数据减去趋势数据，即残差数据
3. 泛克立格插值
   将趋势面分析和残差的克立格插值结果加和，即构成了泛克立格方法分析的结果

协同克里格

【协同克立格分析】是一种空间数据的解释技术，其基本的思想是利用变量之间的空间相关关系进行估计或预测。按照如下的统计准则，它可能是目前最好的空间数据分析方法

1. 真值和估计值之间不存在偏差
2. 估计值具有最小的方差

【要处理的问题是】有两个空间变量，如果第二个变量的分布广，采样密度更高，而第一个变量难以测定或测定的费用较高，那么，可以利用有限样本的变量之间的空间关系来改进对于第一个变量的估计

【步骤】

1. 定义协同变量(第一个变量和第二个变量)
2. 对两个变量进行半方差分析（包括方差图模型），识别观察值的空间关系特征，并用函数模型化
3. 进行交叉半方差分析，确认两个变量相关性
4. 进行空间估计和预测

【评价】协同克立格方法在所使用的变量空间模式与常见的物理过程相联系时最为成功。
【案例】Leenaers etal(1989) 荷兰南北Geul河冲积平原表土重金属(Cd,Pb和Zn)含量分布进行制图

1. 污染物总是吸附于缓慢沉降的细颗粒，因此重金属污染分布在长期停留的地方富集。
2. 结果发现，冲积平原中泛滥河水停留时间最长的地方重金属含量最高，简单地说该区域相对高程与重金属含量有很强的负相关，据此可以利用高程数据进行重金属含量的协同克立格估值插值

【案例】蚁蝗密度的协同克立格分析结果

优缺点仍在争论之中

1. 克立格是一种最优估值技术，数据符合内蕴假设并且方差函数定义得当的条件下。预测误差与其他局部权重方法相比要低
2. “真实”变异越平滑，方差函数拟合和估值越容易，基底方差也越低， 预测误差也低
3. 数据越多，方差函数估计越准确
4. 一旦实验方差函数拟合成理论方差函数，点位和块段克立格插值方差取决于数据空间结构和方差函数模型的形态，而不是数值本身。常规制图方法的预测误差决定于均质区域的确认
5. 块段克立格在点位数据集成到更大区域时非常有用，它通过概括可以降低预测误差
6. 大多数插值技巧，包括克立格，都平滑数据，所以极大和极小值都被去除。这些极端值可能有必要保留
7. 当数据不足时，所有非地统计方法都可以给出一张图。但是你不知道它的质量到底如何。当数据足以计算方差函数时，克立格方法就具有连续变异的独立样点预测方差而言优于其他方法，当变异不连续时，单值景观制图结果可能更好
8. 当数据丰富时，所有插值方法结果相近。效率最高的计算和插值工具就是最好选择。克立格方法的主要困难之一就是缺乏便宜、易用的软件

【解释】克里格强调空间平稳，而空间平稳是受制于某个空间过程，所以克里格肯定是考虑空间过程的

影响因素

1. 数据分布
   正态
2. 空间平稳性
3. 样本数量
   不小于100，分布比较均匀
4. 不同插值方法
   • 点、块
   • 普通、泛、协同、因子、模糊克里格
5. 不同的参数
   • 块金，误差随块金增加
   • 基台，影响不大
   • 变程，存在最佳的变程值
   • 拟合函数，存在最佳的拟合函数

克里格插值的步骤

1. 分析数据的分布特征，进行必要数据转换
2. 分析数据的空间变化趋势
3. 确定变异方差的函数类型
4. 选择合适的搜索半径和临近数据点数，选择合适的插值方法进行插值