本人南航CFD研究生,欢迎加qq:1019003721互相学习讨论!
本文将介绍OpenFOAM里面的大涡模拟相关代码。起因是最近学习OpenFOAM中的大涡模拟,在一篇OpenFOAM中的LES湍流模型及其植入的专栏中看到,但是里面的公式不知道是什么格式,虽然知道一些变量,但一时间也无法弄清楚。因此一边学习张兆顺教授的湍流大涡数值模拟的理论与应用及相关文献,一边看代码校对。(相关文献资料下载)在这期间,看到CFD中文网的李东岳教授发的CFD中的LES湍流模型。这里面讲得非常详细。我将结合上面的内容和OpenFOAM对应的Smagorinsky.C中的代码尽可能仔细地讲解。
LES控制方程
OpenFOAM内含有非常丰富的操作符和算子等。只要确定了控制方程,就能在求解器里自定义要程序解的方程了。在大涡模拟中,省去推导过程,控制方程一般如下形式(张兆顺,2007):
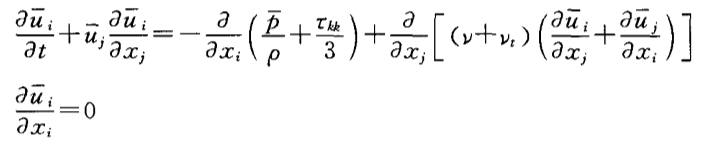
如果写成矩阵形式,引用李东岳的网站:


先看上面的分量形式。在这个控制方程中,要想在OpenFOAM里求解流场变量,仍需要知道
τ
k
k
/
3
\\tau_{kk}/3
τkk/3和
ν
t
\\nu_t
νt才能封闭方程组。在这里,
ν
t
\\nu_t
νt即为亚格子涡粘系数,它在OpenFOAM中是nuSgs。而正应力
τ
k
k
\\tau_{kk}
τkk则可以用亚格子动能代替:
k
s
g
s
=
τ
k
k
/
2
k_{sgs}=\\tau_{kk}/2
ksgs=τkk/2。
k
s
g
s
k_{sgs}
ksgs在OpenFOAM中是k。
Boussinesq假定
具体推导可参照李东岳的博文,这里给出不可压时的结果:

该方程描述了亚格子应力
τ
i
j
\\tau_{ij}
τij和
ν
s
g
s
\\nu_{sgs}
νsgs、
k
s
g
s
k_{sgs}
ksgs的关系。
Smagorinsky模型
在1967年Lilly给出了
τ
k
k
/
3
\\tau_{kk}/3
τkk/3的表达式(相关文献):
τ
k
k
3
=
2
3
ν
s
g
s
2
/
(
C
k
△
)
2
\\frac{\\tau_{kk}}{3}=\\frac{2}{3}\\nu_{sgs}^2/(C_k\\triangle)^2
3τkk=32νsgs2/(Ck△)2
而正应力
τ
k
k
\\tau_{kk}
τkk又可以通过
k
s
g
s
=
τ
k
k
/
2
k_{sgs}=\\tau_{kk}/2
ksgs=τkk/2来替换,最后得到
ν
s
g
s
\\nu_{sgs}
νsgs和
k
s
g
s
k_{sgs}
ksgs的关系:
ν
s
g
s
=
C
k
△
k
s
g
s
\\nu_{sgs}=C_k\\triangle\\sqrt{k_sgs}
νsgs=Ck△ksgs
由此,方程的封闭还差最后一个变量
k
s
g
s
k_{sgs}
ksgs。Smagorinsky提出模型:
S
ˉ
i
j
:
τ
i
j
+
C
e
k
s
g
s
3
2
/
△
=
0
\\bar{S}_{ij}:\\tau_{ij}+C_ek_{sgs}^\\frac{3}{2}/\\triangle=0
Sˉij:τij+Ceksgs23/△=0
通过代入上述各式,即可求解
k
s
g
s
k_{sgs}
ksgs。过程可参考CFD中文网中一二发的帖子。
Ps:运算符“:”是双重内积,即两张量先作矩阵乘法运算(点积),再进行缩并(Contraction)。因为参与运算的两个张量都是二阶,点积后仍为二阶,但缩并后降二阶,最后是零阶,即一个数。最后这个方程是一个一元二次方程,按公式法求解即可。
在此引用一二发的帖子中的结果:

OpenFOAM中代码
在OpenFOAM中,公式与上文所述一致,只是所用的变量名字不同:
\\verbatim
B = 2/3*k*I - 2*nuSgs*dev(D)
where
D = symm(grad(U));
k from D:B + Ce*k^3/2/delta = 0
nuSgs = Ck*sqrt(k)*delta
\\endverbatim
B就是
τ
i
j
\\tau_{ij}
τij,D就是
S
i
j
S_{ij}
Sij。
在Smagorinsky.C的代码中,先计算了
k
s
g
s
k_{sgs}
ksgs:
template<class BasicTurbulenceModel>
tmp<volScalarField> Smagorinsky<BasicTurbulenceModel>::k
(
const tmp<volTensorField>& gradU
) const
{
volSymmTensorField D(symm(gradU));
volScalarField a(this->Ce_/this->delta());
volScalarField b((2.0/3.0)*tr(D));
volScalarField c(2*Ck_*this->delta()*(dev(D) && D));
return volScalarField::New
(
IOobject::groupName("k", this->alphaRhoPhi_.group()),
sqr((-b + sqrt(sqr(b) + 4*a*c))/(2*a))
);
}
代码中abc都与上面的结果一一对应。
再计算
ν
s
g
s
\\nu_{sgs}
νsgs并修正控制方程中的nut:
template<class BasicTurbulenceModel>
void Smagorinsky<BasicTurbulenceModel>::correctNut()
{
volScalarField k(this->k(fvc::grad(this->U_)));
this->nut_ = Ck_*this->delta()*sqrt(k);
this->nut_.correctBoundaryConditions();
fv::options::New(this->mesh_).correct(this->nut_);
BasicTurbulenceModel::correctNut();
}
correctNut()在各求解器中都会有的,在计算完这一时间步之后,修正湍流粘度系数,作下一时间步所用。这就是OpenFOAM植入湍流模型的逻辑:在不改变其控制方程的情况下,只修改湍流粘度系数,就能达到计算湍流的目的。
参数
C
k
C_k
Ck在Lilly(1967)的文章中是0.094,和OpenFOAM中的对应。而
C
e
C_e
Ce的来源尚不清楚,博文说
C
e
=
1.048
C_e=1.048
Ce=1.048是因为湍流模型基于GenEddyVisc model(一般涡粘性假设?),如有误,请加qq1019003721进行勘误,谢谢!
参考文献
- Smagorinsky J. General circulation experiments with the primitive
equations: I. the basic experiment[J]. Monthly weather review, 1963,
91(3): 99-164. - Smagorinsky, J. , Manabe, S. , & Holloway, J. L. . (1963).
“numerical results from a nine-layer general circulation model,”.
monthly weather review, 91(12), 263-270. - Deardorff, J. W. . (1970). A numerical study of three-dimensional
turbulent channel flow at large reynolds number. Journal of Fluid
Mechanics, 41. - LILLY, D. K. 1967 Proceedings of the IBM Scientific Computing
Symposium on Environmental Sciencer, IBM Form no. 320-1951, 195. - 张兆顺, 崔桂香, 许春晓. 湍流大涡数值模拟的理论与应用[M]. 清华大学出版社, 2008.
其中1235可以在我上传的文件中下载。
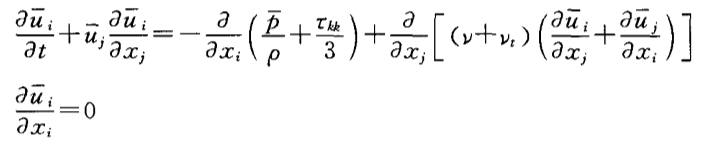







![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)