3D多面体表面

1 概述

三维多面体表面由顶点、边、面及其上的关联关系组成，基于半边数据结构设计。多面体表面可以看作为一个容器类，它管理顶点、半边、小平面及其入射关系，并保持它们的组合完整性。

一个三维的多面体表面Polyhedron_3<PolyhedronTraits_3> 由顶点V、边E、面F和它们上的入射关系组成。每条边由两个方向相反的半边表示。使用半边存储的关系如下图所示：

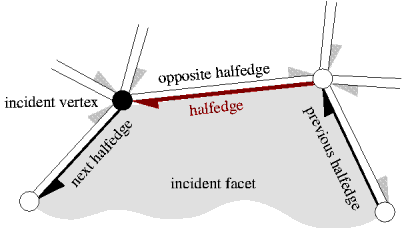
• 按照惯例，从多边形外部看，半边沿逆时针方向围绕面。
• 自相交不容易有效地被检测到。
• Polyhedron_3<PolyhedronTraits_3> 仅保持多面体表面的组合完整性（使用欧拉运算），不考虑点的坐标或任何其他几何信息。

很多栗子

第一个简单例子

#include <CGAL/Simple_cartesian.h>
#include <CGAL/Polyhedron_3.h>
typedef CGAL::Simple_cartesian<double>     Kernel;
typedef CGAL::Polyhedron_3<Kernel>         Polyhedron;  //通过使用内核作为特征类
typedef Polyhedron::Halfedge_handle        Halfedge_handle; //半边句柄
int main() {
    Polyhedron P;
    Halfedge_handle h = P.make_tetrahedron();   //返回P的任意半边
    if (P.is_tetrahedron(h))                    //检查h是否属于多面体表面
        return 0;
    return 1;
}

顶点迭代器的使用

#include <CGAL/Simple_cartesian.h>
#include <CGAL/Polyhedron_3.h>
#include <iostream>
typedef CGAL::Simple_cartesian<double>     Kernel;
typedef Kernel::Point_3                    Point_3;
typedef CGAL::Polyhedron_3<Kernel>         Polyhedron;
typedef Polyhedron::Vertex_iterator        Vertex_iterator;
int main() {
    Point_3 p( 1.0, 0.0, 0.0);
    Point_3 q( 0.0, 1.0, 0.0);
    Point_3 r( 0.0, 0.0, 1.0);
    Point_3 s( 0.0, 0.0, 0.0);
    Polyhedron P;
    P.make_tetrahedron( p, q, r, s);
    CGAL::IO::set_ascii_mode( std::cout);
    for ( Vertex_iterator v = P.vertices_begin(); v != P.vertices_end(); ++v)
        std::cout << v->point() << std::endl;
    return 0;
}

我们也可以使用std::copy 和 ostream 迭代器适配器简化for遍历：

std::copy( P.points_begin(), P.points_end(),std::ostream_iterator<Point_3>(std::cout,"\\n"));

多面体的绘制

draw_polyhedron.cpp

#include <CGAL/Exact_predicates_inexact_constructions_kernel.h>
#include <CGAL/Polyhedron_3.h>
#include <CGAL/IO/Polyhedron_iostream.h>
#include <CGAL/draw_polyhedron.h>
#include <fstream>
typedef CGAL::Exact_predicates_inexact_constructions_kernel  Kernel;
typedef CGAL::Polyhedron_3<Kernel>                       Polyhedron;
int main(int argc, char* argv[])
{
  Polyhedron P;
  std::ifstream in1((argc>1)?argv[1]:CGAL::data_file_path("meshes/cross_quad.off"));
  in1 >> P;
  CGAL::draw(P);
  return EXIT_SUCCESS;
}