B-样条曲线：定义

B-spline Curves: Definition

给定 n + 1个控制点P₀, P₁, …, P_n 和一个节点向量U = { u₀, u₁, …, u_m }, p 次B-样条曲线由这些控制点和节点向量U 定义

其中 N_i,p(u)是 p次B-样条基函数。 B-样条曲线形式与贝塞尔曲线相似。不像贝塞尔曲线, B-样条曲线包含更多信息，即：一系列的 n+1 个控制点， m+1个节点的节点向量，次数 p。注意n, m 和 p 必须满足m = n + p + 1。更准确地，如果我们想要定义一个有 n + 1控制点的p次B-样条曲线，我们必须提供n + p + 2 个节点 u₀, u₁, …, u_n+p₊₁。另一方面，如果给出了一个m + 1 个节点的节点向量和n + 1 控制点，B-样条曲线的次数是p = m – n – 1。对应于一个节点u_i的曲线上的点， C(u_i)，被称为节点点（knot point）。因此，节点点把B-样条曲线划分成曲线段，每个都定义在一个节点区间上。我们将在曲线细分页证明这些曲线段都是 p 次的贝塞尔曲线。

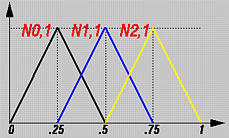
尽管 N_i,p(u) 看起来像B_n,i(u)， B-样条基函数的次数(degree)是一个输入数，而贝塞尔基函数的次数取决于控制点的数目。为了改变B-样条曲线的形状，可以修改一个或多个控制参数：控制点的位置，节点位置，和曲线的次数。

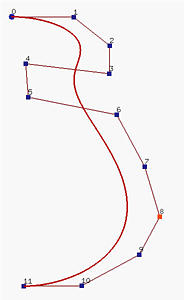
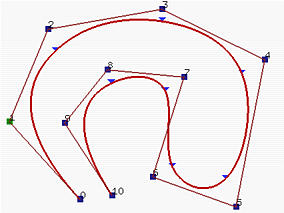
如果节点向量没有任何特别的结构，那么产生的曲线不会与控制折线（polyline）的第一边（leg）和最后一边（leg）接触，如下面左图所示。这种类型的B-样条曲线称为开（open ）B-样条曲线。我们可能想强制曲线使得它分别与第一个控制点和最后一个控制点的第一边和最后一边相切，像贝塞尔曲线那样。为了做到这些，第一个节点和最后一个节点必须是重复度为p+1。这就产生了所谓的clamped B-样条曲线。参见下边中间的图。通过重复某些节点和控制点，产生的曲线会是闭（closed）曲线。这种情况，产生的曲线的开始和结尾连接在一起形成了一个闭环如下边右图所示。在本文中，我们将使用clamped曲线。

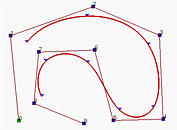
上图有 n+1个控制点(n=9)以及 p = 3. 。那么，, m 必须是13 所以节点向量有14个节点。为了有clamped效果，前p+1 = 4 和最后4个节点必须一样。其余14 – (4 + 4) = 6 个节点可在定义域任何位置。实际上，曲线是用节点向量 U = { 0, 0, 0, 0, 0.14, 0.28, 0.42, 0.57, 0.71, 0.85, 1, 1, 1, 1 }产生的。注意除了头四个和最后四个节点，中间的节点几乎是均匀分布的。图形也显示了每个节点区间上的相应的曲线段。实际上，小三角是节点点。

术语的使用

我们使用开（open）， clamped 和闭（closed）来描述三种类型的B-样条曲线。但是，不是每一个作者都会使用相同的术语，并没有一个标准用法的共识。例如，有些作者会使用 floating, open 和 periodic 来称呼开（open）, clamped 和闭（closed）曲线。其他有些作者会使用"periodic"来称呼一个有均匀节点序列的开（open）B-样条曲线。因此，当你读其他文献时，首先要看其定义。否则，你很可能会感到困惑。

下面继续 开（open）曲线和 闭（closed）曲线。

译注：

本文翻译是“B-样条曲线（B-spline Curves）教程”中的一部分，其余翻译部分见“B-样条曲线（B-spline Curves）教程目录”。
“B-样条曲线（B-spline Curves）教程”是翻译自C.-K. Shene博士的CS3621 Introduction to Computing with Geometry Notes的第6部分“B-spline Curves”。
本文原文地址：B-spline Curves: Definition 。
本文首发“博士数学家园 ”