B-样条曲线条：闭曲线

B-spline Curves: Closed Curves

上一页开曲线               回目录                        下一页重要性质    

有许多方法来产生闭曲线。简单的一种就是或者wrapping控制点或者wrapping节点向量。

Wrapping控制点

假设我们想构建一个p次闭（closed）B-样条曲线C(u)，由n+1 控制点P₀, P₁, …, P_n.定义。节点数目是m+1, 其中 m = n + p + 1. 这儿是构建过程：

1. 设计一个均匀 m+1 个节点的节点序列：u₀ = 0, u₁ = 1/m, u₁ = 2/m, …, u_m = 1。注意曲线的定义域是 [u_p, u_n-p]. 详见开（open）曲线的讨论。
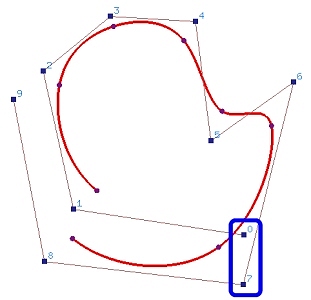
2. Wrap头p 个和最后p 个控制点。更准确地，设P₀ = P_n–p+1, P₁ = P_n–p+2, …, P_p-2 = P_n-1 and P_p-1 = P_n. 如下图所示。

构建的曲线在连接点处 C(u_p) = C(u_n-p)是C^p-1 连续的。.

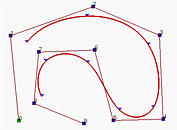
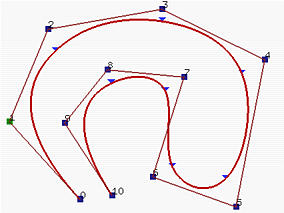
下面举个例子图 (a) 显示了一个由10（n=9）个控制点和一个均匀节点向量定义的3次开（open）B-样条曲线。在图中，控制点对0 和7, 1和8, 以及2和9放置在相互靠近的地方来说明这个构建。图 (b) 显示了使得点0和7重叠的结果。 曲线的形状没有太大变化。那么，控制点1和8重叠如图(c)所示。很显然曲线的第一点和最后一点的间距更近了。最后曲线变成一个闭曲线当控制点2和9重叠后，如图(d)所示。

Wrapping 节点

另一种构建闭B-样条曲线的方法是wrapping节点。假设我们想要构建一个由n+1个控制点P₀, P₁, …, P_n定义的p 次闭B-样条曲线C(u) 。构建过程如下：

1. 增加一个新控制点 P_n+1 = P₀.因此，控制点的数目是 n+2.
2. 找到一个合适的有 n+1节点的节点序列u₀, u₁, …, u_n 。这些节点不必要是均匀的，an advantage over the method discussed above。
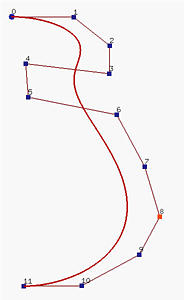
3. 增加 p+2 个节点并 wrap 头 p+2个节点： u_n+1 = u₀, u_n+2 = u₁, …, u_n+p = u_p-1, u_n+p+1 = u_p, u_n+p+2 = u_p+1 ，如下图所示。这样，我们有n+p+2 = (n+1) + p + 1 个节点。
4. 定义在上述构建的 n+1个控制点和n+p+2 个节点上的 p 次开B-样条曲线C(u)是一个闭曲线，在连接点处C(u0) = C(un+1)有Cp-1 连续性。注意闭曲线的定义域是 [u₀, u_n+1].

上一页开曲线               回目录                        下一页重要性质     

译注：   

1. 1.  本文翻译是“B-样条曲线（B-spline Curves）教程”中的一部分，其余翻译部分见“B-样条曲线（B-spline Curves）教程目录”。
   2.  “B-样条曲线（B-spline Curves）教程”是翻译自C.-K. Shene博士的CS3621 Introduction to Computing with Geometry Notes的第6部分“B-spline Curves”。
   3. 本文原文地址：B-spline Curves: Closed Curves   。
   4. 本文首发“博士数学家园 ”