B-样条曲线：重要性质

B-spline Curves: Important Properties

B-样条曲线有很多与贝塞尔曲线一样的重要性质，因为前者是后者的推广。而且，B-样条曲线有比贝塞尔曲线更渴望的性质。下面列出B-样条曲线一些最重要的性质。

接下来我们假设一个由n + 1 控制点和一个节点向量U = { u₀, u₁, …., u_m } 定义的 p次B-样条曲线C(u)，其中头p+1个和最后 p+1个节点是 "clamped" (即，u₀ = u₁ = … = u_p 和 u_m-p = u_m-p₊₁ = … = u_m).

1. B-样条曲线是个逐段曲线，每个分量是p次曲线。
如前页提到的， C(u) 可看作是定义在每个节点区间的曲线段的联合。在下图中，其中n = 10, m = 14 和 p = 3, 头四个节点和最后四个节点是clamped而中间7个节点上均匀分布的。有8个节点区间，每个对应于一个曲线段。在下面左图，这些节点点以三角形标示。

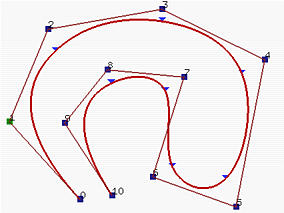
这个良好性质使得我们可以以更低次多项式来设计复杂形状。例如，下面右图显示了相同控制点的贝塞尔曲线。即使在其次数达到10仍然不能很好逼近控制折线（polyline）!

一般，次数越低，B-样条曲线越逼近它的控制折线（polyline）。下图都使用相同的控制折线（polyline）且节点是 clamped且均匀分布。第一个图是7次，中间的是5次而右图是3次。因此，当次数减小，产生的B-样条曲线越接近它的控制折线（polyline）。

2. 等式 m = n + p + 1必须满足。
由于每个控制点需要一个基函数且基函数数目满足 m = n + p + 1。.

3. Clamped B-样条曲线C(u)通过首尾两个控制点 P₀ 和P_n 。
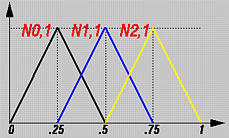
注意基函数N_0,p(u) 是控制点 P₀ 的系数且在[u₀,u_p₊₁)上非零因为对于一个clamped B-样条曲线有 u₀ = u₁ = … = u_p = 0， N_0,0(u), N_1,0(u), …., N_p_-1,0(u)为零且只有 N_p_,0(u)是非零（回忆三角计算格式）因此，如果u = 0，那么N_0,p(0)是1且C(0) = P₀。相似地可得到C(1) = P_n 。

4. 样条曲线包含在控制折线（ployline）的凸包内。更特别地，如果u 在节点区间[u_i,u_i₊₁)里，那么C(u)在控制点P_i-p, P_i-p₊₁, …, P_i的凸包里。
如果u 在节点区间 [u_i, u_i₊₁)里，那么只有p+1 个基函数(即，N_i_,p(u), … , N_i-p_+1,p(u), N_i-p_,p(u))在该节点区间非零。因为 N_k,p(u) 是控制点 P_k的系数，只有 p+1个控制点 P_i, P_i_-1, P_i_-2, .., P_i-p 有非零系数。因为在该节点区间上的基函数非零且累加和为 1,它们的“权重”平均（ "weighted" average）， C(u), 必须位于由控制点 P_i, P_i_-1, P_i_-2, .., P_i-p定义的凸包内。 “强”的意思是当 C(u) 仍位于由所有控制点定义的凸包内，它位于更小的里面。

上面两个 B-样条曲线有11个控制点(即，n = 10), 3次 (即， p=3) 及15 个节点 (m = 14)，其中头四个和最后四个节点是 clamped。因此，节点区间的数目等于曲线段的数目。节点向量是

u₀	u₁	u₂	u₃	u₄	u₅	u₆	u₇	u₈	u₉	u₁₀	u₁₁	u₁₂	u₁₃	u₁₄
0	0	0	0	0.12	0.25	0.37	0.5	0.62	0.75	0.87	1	1	1	1

左图有u 在节点区间 [u₄, u₅) = [0.12,0.25)上且相应的点(即 C(u))在第二条曲线段上。因此，有p+1 = 4 个基函数在给节点区间(即，N_4,3(u), N_3,3(u), N_2,3(u) 和 N_1,3(u) )上非零且相应的控制点是P₄, P₃, P₂ and P₁。阴影部分是由这四个点定义的凸包。很清楚C(u) 位于凸包内。

右图的B-样条曲线同样方式定义。但是，u 是在[u₉, u₁₀) = [0.75,0.87)上且非零基函数是 N_9,3(u), N_8,3(u), N_7,3(u) 和N_6,3(u)。相应的控制点是 P₉, P₈, P₇ 和 P₆。

因此，当 u 从 0移到1并越过一个节点时，一个基函数变为零而一个新的非零基函数开始有效。结果是，系数变为零的控制点会离开当前凸包的定义而被一个新的系数变为非零的控制点所代替。.

5. P_i 只影响在区间[u_i, u_i+p₊₁)上的曲线 C(u)。.
这是从B-样条基函数的一个重要性质得到。回忆N_i,p(u) 在区间[u_i, u_i+p₊₁)上非零。. 如果u 不在该区间， N_i,p(u)P_i 在计算computing C(u)时没有作用因为 N_i,p(u)是零。另一方面，如果u 是指示的区间， N_i,p(u) 非零。如果 P_i 改变它的位置， N_i,p(u)P_i 被改变导致C(u)被改变。

上面B-样条曲线以在前面凸包例子一样的参数定义。我们想移动控制点P₂ 。控制点的系数是N_2,3(u) 且有非零系数在其上的区间是 [u₂, u₂₊₃₊₁) = [u₂, u₆) = [0,0.37)。因为 u₂ = u₃ = 0，只有三段被影响，分别是对应 u₃, u₄) 的(第一个曲线段的定义域), [u₄, u₅) (第二个曲线段的定义域) 和[u₅, u₆) (第三个曲线段的定义域) 。右图显示的是移动 P₂ 到右下角的结果。正如你看到的，只有第一，第二和第三曲线段改变了形状而剩余其他曲线段保持在原来位置没有改变。

局部修改方案对曲线设计非常重要，因为我们可以局部修改曲线而不需全局改变形状。这将在 moeing control point 页详细说明。而且，如果需要更精细调整曲线形状，可以插入更多节点（因而更多控制点）以至于被影响的区域被限制在很窄区域。以后我们会谈到节点插入。

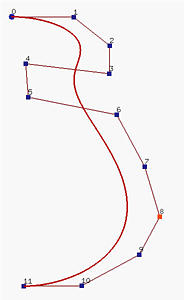
6. C(u) 在重复度 k 的节点上是C^p-k 连续的
如果 u 不是一个节点， C(u) 是p 次曲线段的中部因而是无限可微的。如果 u 是在 N_i,p(u)的非零定义域中的一个节点，既然后者是C^p-k 连续的，C(u)也一样。

上图B-样条曲线有18个控制点 (即， n = 17), 4次（degree），clamped节点向量如下

u₀ to u₄	u₅	u₆ and u₇	u₈	u₉ to u₁₁	u₁₂	u₁₃ to u₁₆	u₁₇	u₁₈ to u₂₂
0	0.125	0.25	0.375	0.5	0.625	0.75	0.875	1

因此， u₆ 是一个双重节点， u₉是一个三重节点而u₁₃ 是一个四重节点。因此， C(u) 在不是节点的任何点是 C⁴ 连续的，在所有简单节点处 C³ 连续的，在 u₆是C² 连续的，在u₉ 是 C¹ 连续的，在u₁₃是 C⁰ 连续的。

在曲线上与节点相对应的所有点用小三角标记。那些对应于多重节点的点用圆和重复度标记。要可视化 C⁴, C ³ 和甚至C² 连续性之间的差别是很困难的。对 C¹ 情况，相应的点位于一条边（leg）上，而 C⁰ 情况迫使曲线通过一个控制点。我们会在后面讨论修改节点时返回这个问题。

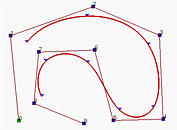
7. 变分减小性质：
变分减小性质度对B-样条曲线也成立。如果曲线在平面(resp., 空间)上，这意味着没有直线(resp., 平面) 与 B-样条曲线相交的次数多于它与曲线控制折线（polyline）相交的次数。

在上图中，蓝线与控制折线（polyline）和B-样条曲线都相交6次，而黄线也与控制折线和B-样条曲线相交 5次。但是，橘黄线与控制折线相交 6次和曲线相交4次。

8. 贝塞尔曲线是B-样条曲线的特例。
如果 n = p (即，B-样条曲线的次数是n, 控制点的数目减1有 2(p + 1) = 2(n + 1)个节点，其中 p + 1个在端（end）处clamped，这个B-样条曲线退化到贝塞尔曲线。

9. 仿射不变性
仿射不变性对B-样条曲线也成立。如果一个仿射变换应用于B-样条曲线，得到的结果可以从它的控制点的仿射像（images）构建得到。这是一个好性质。当我们要对B-样条曲线应用一个几何或仿射变换，这条性质说明我们可以对控制点进行变换，而这相当容易，而且一旦获得了这些变换后的控制点，变换B-样条曲线就是这些新点定义的。因此，我们不需要对曲线进行变换。

使用B-样条曲线的优点

B-样条曲线比贝塞尔曲线需要更多信息(即，曲线的次数和一个节点向量 )和更复杂的理论。但是它有更多优点来弥补这个缺点。第一，一个B-样条曲线可以是一个贝塞尔曲线。第二，B-样条曲线满足贝塞尔曲线有的所有重要性质。第三，B-样条曲线提供了比贝塞尔曲线更灵活的控制。例如，一个B-样条曲线的次数与控制点数目是分开的。更准确地说，我们可以使用更低次曲线而仍然保持很多控制点。我们可以改变一个控制点位置而不会全局地改变整个曲线形状（局部修改性质）。因为B-样条曲线满足强凸包性质，它们可以进行更精细的形状控制。而且，还有其他设计和编辑形状的技术比如改变节点。

但是，记住B-样条曲线仍然是多项式曲线而多项式曲线不能表示许多有用的简单的曲线比如圆和椭圆。因此，需要B-样条的一个推广，NURBS。后面会讨论 NURBS 。

译注：

本文翻译是“B-样条曲线（B-spline Curves）教程”中的一部分，其余翻译部分见“B-样条曲线（B-spline Curves）教程目录”。
“B-样条曲线（B-spline Curves）教程”是翻译自C.-K. Shene博士的CS3621 Introduction to Computing with Geometry Notes的第6部分“B-spline Curves”。
本文原文地址：B-spline Curves: Important Properties 。
本文首发“博士数学家园 ”