B-样条曲线：系数计算

B-spline Curves: Computing the Coefficients

尽管de Boor算法是一个计算对应于给定u的B-样条曲线上的点的标准方法，我们许多情况下（例如，曲线插值和逼近）真正需要的是这些系数。我们将阐述一个简单方法来做这个。

给定一个由 n+1个控制点P₀, P₁, …, P_n, 和 m+1个节点 u₀=u₁=…=u_p=0, u_p₊₁, u_p₊₂, …, u_m-p_-1, u_m-p=u_m-p₊₁=…= u_m=1定义的p 次clamped B-样条曲线。对于任何给定在[0,1]上的 u ，我们想计算系数N_0,p(u), N_1,p(u), …, N_n,p(u) 。一个简单方法是使用下列递推关系：

但是这是一个非常耗时的过程。为了计算 N_i,p(u), 我们需要计算 N_i,p_-1(u)和N_i_+1,p-1(u). 为了计算N_i,p_-1(u), 我们需要计算N_i,p_-2(u) 和 N_i_+1,p-2(u). 为了计算N_i_+1,p-1(u), 我们需要N_i_+1,p-2(u)和 N_i_+2,p-2(u). 如你们所看到的， N_i_+1,p-2(u)出现了两次，因此，递归计算会重复。当递归继续深入，会出现更多的重复计算。这与在前页讨论的de Casteljau算法的递归版本很相似。因此，计算速度非常慢。

有容易的方法。设 u 在节点区间[u_k,u_k₊₁)上。. B-样条基函数的重要性质说明最多 p+1个p 次基函数在[u_k,u_k₊₁)上非零，即： N_k-p,p(u), N_k-p_+1,p(u), N_k-p_+2,p(u), …, N_k_-1,p(u), N_k_,p(u)。通过定义，在 [u_k,u_k₊₁)上的0次仅有的非零基函数是N_k_,0(u)。结果，从.N_k_,0(u)出发计算系数是以一个 "fan-out" 三角形式，如下图所示：

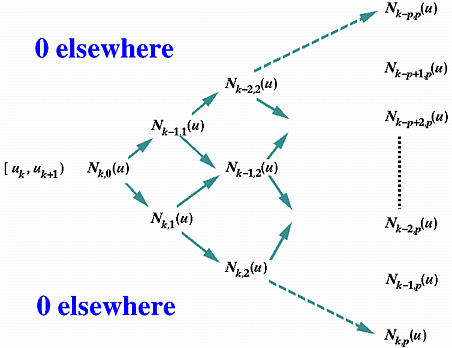
因为在 [u_k,u_k₊₁)上 N_k_,0(u) = 1而其他0次B-样条基函数在[u_k,u_k₊₁)上是零，我们可以从 N_k_,0(u)开始而计算1次基函数 N_k_-1,1(u) 和 N_k_,1(u)。从这两个值，我们可以计算2次基函数 N_k_-2,2(u), N_k_-1,2(u) 和N_k_,2(u)。这个过程重复直到所有p+1 个非零系数计算出来。

在这个计算中， “内部”值如 N_k_-1,2(u)有一个西北向前驱 (即， N_k_-1,1(u))和一个西南向的前驱 (即， N_k_,1(u))；上述三角如N_k_-1,1(u)的东北方向边界上的值只有一个西南向前驱 (即， N_k_,0(u))；这个三角如 N_k_,2(u)的东南方向边界上的值只有一个西北前驱 (即， N_k_,1(u))。因此，在东北 (resp., 东南)方向边界上的值使用定义中的递归关系的第二 (resp., 第一)项。只有内部值使用全部两项。基于这个观察，我们有下列算法：

输入： n, p, m, u, 和 m+1个 clamped 节点 { u₀, …, u_m }
输出：系数N_0,p(u), N_1,p(u), …, N_n,p(u) 在 N[0], N[1], …, N[n]
算法：

初始化 N[0..n] 为 0; // 初始化
if u = u₀ then // 排除特例

N[0] = 1.0;
return

else u = u_m then

N[n] = 1.0
return

end if

// 现在u 在 u₀ 和 u_m 之间

设 u 在节点区间[u_k,u_k₊₁);
N[k] := 1.0 // 0次系数
for d :=1 to p do // 次数 d 从1 到 p

begin

N[k-d] = * N[(k-d)+1]; // 仅右边 (东南角)项
for i := k-d+1 to k-1 do // 计算中间项

N[i] := * N[i] + * N[i+1];

N[k] = * N[k]; // 仅左边 (西北角) 项

end

// 数组 N[0..n] 有系数。

上述算法不是很有效的算法。它的目的是为了以一个直觉容易理解的方式说明思想。数组N[ ] 保存所有中间值和最后结果。对一个次数 d, N[i] 保存了N_i,d(u)的值，且，最后，N[k-d], N[k-d+1], …, N[k] 含有非零系数。计算以 d=1开始因为我们知道仅有的非零基函数是 N_k_,0(u)如果 u 在节点区间 [u_k,u_k₊₁)上。外循环使得次数 d 从 1到 p。 begin 后面的第一次赋值是仅使用一项(即，三角中的西南项， N_k-d_+1,d-1(u))，计算 N_k-d_,d(u) ，内部 for 循环计算 “内部”项，而外循环中最后一个语句仅使用一项(即，三角中的西北项， N_k,d_-1(u)) 计算 N_k,d(u)。

你能使这个算法更有效吗?

译注：

- 本文翻译是“B-样条曲线（B-spline Curves）教程”中的一部分，其余翻译部分见“B-样条曲线（B-spline Curves）教程目录”。
- “B-样条曲线（B-spline Curves）教程”是翻译自C.-K. Shene博士的CS3621 Introduction to Computing with Geometry Notes的第6部分“B-spline Curves”。
- 本文原文地址：B-spline Curves: Computing the Coefficients 。
- 本文首发“博士数学家园 ”