B-样条曲线:特例
B-spline Curves: A Special Case
上一页系数计算 回目录 下一页移动控制点

如果我们有 2n+2 个节点 u0 = u1 = … = un = 0及 un+1 = un+2 = … = u2n+1 = 1 (即,头 n+1 个是零,而后 n+1是1), n 次B-样条基函数是什么?
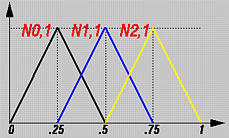
因为每个 u 在 [0,1] = [un, un+1]上, n 次非零基函数是: N0,n(u), N1,n(u), …, Nn,n(u)。回忆B-样条基函数的定义如下:
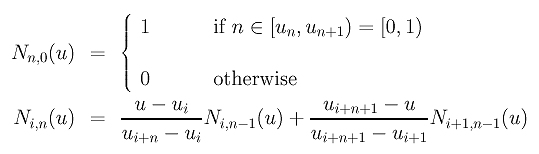
因为仅有的 0次非零基函数是Nn,0(u),下标 i 只能在0 和n之间。因此, ui是零而 ui+n和ui+n+1是1。结果,上边第二个等式可重写为如下式:

如果我们进行如前页讨论的那样以一个三角形式计算N0,n(u), N1,n(u), …, Nn,n(u) ,那么我们有下图。在该图中,每个东北(resp., 东南)边界箭头意味这乘1-u (resp., u)到在箭头尾部的项上。注意计算中有n 步骤,每步获得每列。因此, Nn,0(u) 对 N0,n(u)的贡献是 (1-u)n, 而Nn,0(u)的贡献对Nn,n(u)是un.

现在,考虑一般项 Ni,n(u)的计算。 Nn,0(u) 对Ni,n(u)计算的贡献可用"path-counting"技术确定,其用来展示de Casteljau算法的正确 以及贝塞尔曲线的更高次导数的计算中。每个从 Nn,0(u) 到 Ni,n(u) 遇n 箭头其中i 是东南边界 而 n-i 是东北边界。 那些东北(resp., 东南)边界箭头意味着对尾部的项乘以1-u (resp., u)。因此,Nn,0(u) 对 Ni,n(u)的贡献沿着一个单path是 ui(1-u)n-i 。从 Nn,0(u) 到 Ni,n(u)的paths总数是C(n,i)。更准确地,paths的数目等于放置 i 个东南边界箭头在n 个位置不同方法的数目。剩余 n-i 位置用东北边界箭头充满。这 n 个箭头准确地描述了从 Nn,0(u) 到 Ni,n(u)的一个单路径(path)。因为每个路径(path)贡献 ui(1-u)n-i 给计算且因为有C(n,i) 个路径,Nn,0(u) 对 Ni,n(u)的总贡献是

这就是 n次第i个贝塞尔基函数。因此,我们有下列结论:
| 对所有在 0和n范围内的 i ,如果头 (resp., 最后) n+1节点等于 0 (resp., 1), 那么n次第i个B-样条基函数与第i个贝塞尔基函数是一致的。因此贝塞尔基函数是B-样条基函数的特例,而贝塞尔曲线是B-样条曲线的特例。 |
译注:
- 本文翻译是“B-样条曲线(B-spline Curves)教程”中的一部分,其余翻译部分见“B-样条曲线(B-spline Curves)教程目录”。
- “B-样条曲线(B-spline Curves)教程”是翻译自C.-K. Shene博士的CS3621 Introduction to Computing with Geometry Notes的第6部分“B-spline Curves”。
- 本文原文地址:B-spline Curves: A Special Case 。
- 本文首发“博士数学家园 ”
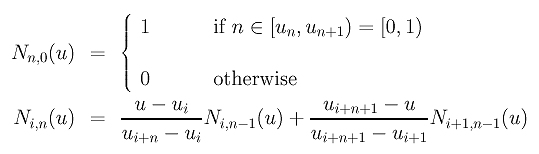







![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)





暂无评论内容