B-样条曲线的导数

Derivatives of a B-spline Curve

上一页修改节点                 回目录                         下一页单个插入    

尽管B-样条曲线比贝塞尔曲线复杂得多，它们的导数很相似。假设一个B-样条曲线定义如下：

每个基函数的导数可计算如下：

将这些导数代回曲线方程得到下列结果：

其中 Q_i定义如下：

因此，一个B-样条曲线的导数是另一个p – 1次B-样条曲线，在原来的节点向量上，而有新的n 个控制点Q₀, Q₁, …, Q_n-1。

如果原始的clamped节点向量是u₀(p+1), u_p+1, …, u_m-p-1, u_m(p+1)，那么移动第一个和最后一个节点使得第一个和最后一个节点重复度变成, p 而不是p+1，我们有一个m – 1 个节点u₀(p), u_p+1, …, u_m-p-1, u_m(p)的新节点序列。那么，可证明在原来节点序列计算的N_i+1,p-1(u) 等于在新节点序列上的N_i,p-1(u)。因此，在新节点序列上的一个B-样条曲线的导数如下：

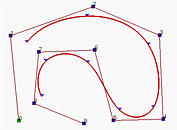
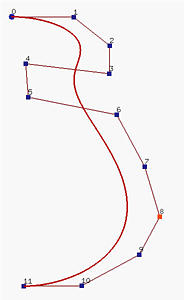
下面左图是一个5次的B-样条曲线。它的导数曲线，其是一个由新 n 个控制点定义的 p-1次B-样条曲线，显示在中图。如同贝塞尔曲线的情况，这是一个原始曲线的矢端曲线（hodograph）。下面右图显示的是控制折线删除后的矢端曲线（hodograph）。 

我们知道一个clamped B-样条曲线经过第一个和最后一个控制点。实际上，它也与控制折线的第一边和最后一边相切。回忆上面的p 次B-样条曲线C(u)的导数是

其节点向量通过将第一个节点和最后一个节点从原始节点序列去掉获得。因此，第一个(和最后一个)节点的重复度是p，因此，上面的 p-1次B-样条曲线是clamped。因为一个clamped B-样条曲线经过它的第一个和最后一个控制点，我们有C'(0) = Q₀ 和 C'(1) = Q_n-1。 因为，对i = 0有 u₀ = …. = u_p = 0 ，所以我们有

因此，在C'(0)上的切向量与从P₀ 到 P₁ 的向量有相同的方向，而 C(u) 与第一边相切。基于同样的推理，我们有下列结果：

因此，C(u) 与最后一边相切。总之，我们有下列重要事实： 

因为一个B-样条曲线的一阶导数是另一个B-样条曲线，所以可以毫无困难地递归应用该技术来计算更高阶导数。

上一页修改节点                 回目录                         下一页单个插入    

译注：