【XJTUSE计算机图形学】第二章光栅图形学(2)—消隐

基本概念

投影变换失去了深度信息，往往导致图形的二义性

消隐：为了消除二义性，必须在绘制时消除被遮挡的不可见的线或面，习惯上称作消除隐藏线和隐藏面；

经过消隐得到的投影图称为物体的真实图形。

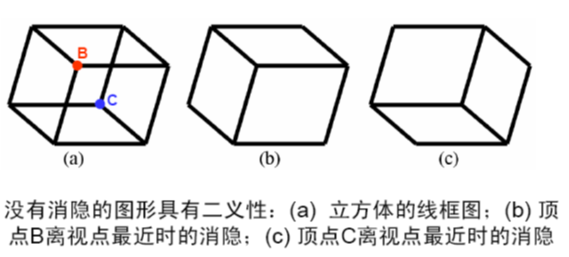
消隐的对象是三维物体。三维体的表示主要有边界表示和构造实体几何表示等。

最简单的方法：用表面上的平面多边形表示。

消隐结果与观察物体有关，也与视点有关。

几个假设

1️⃣ 投影平面是oxy平面；

2️⃣ 投影方向为负z轴方向的平行投影；

值越大，离视点越近；

透视变换转化为平行投影。

3️⃣ 不能处理相互贯穿或循环遮挡的物体，此时应做特殊处理。

在实时模拟过程中，要求消隐算法速度快，通常生成的图形质量一般；

在真实感图形生成过程中，要生成高质量的图形，通常消隐算法速度较慢。

消隐算法的权衡：消隐效率、图形质量。

与消隐与密切相关的因素

物体排序：判断场景中的物体全部或者部分与视点之间的远近；

连贯性：场景中物体或其投影所表现出来的相似程度。

提高消隐算法效率的常见方法

利用连贯性、包围盒技术、背面剔除、空间分割技术、物体分层表示

利用连贯性

利用连贯性：相邻事物的属性之间有一定的连贯性，其属性值通常是平缓过渡的，如颜色值、空间位置关系等

物体连贯性

面的连贯性

区域连贯性

扫描线的连贯性

深度连贯性

包围盒技术

一个形体的包围盒指的是包围它的简单形体

假设包围和充分紧密包围着形体；

对其的测试比较简单。

常用包围盒:长方体、球、圆柱

背面剔除

外法向：规定每个多边形的外法向都是指向物体外部的。

前向面：若多边形的外法向与投影方向（观察方向）的夹角为钝角（V· N<0），称为前向面。

后向面：若多边形的外法向与投影方向（观察方向）的夹角为锐角（V· N>0），称为后向面（背面）。

后向面总是看不见的，不会由于后向面的遮挡，而使别的棱成为不可见的。因此计算时，可以把这些后向面全部去掉，这并不影响消隐结果。

空间分割技术

将投影平面上的窗口分成若干小区域；为每个小区域建立相关物体表，表中物体的投影于该区域有相交部分；则在小区域中判断那个物体可见时，只要对该区域的相关物体表中的物体进行比较即可

物体分层表示

减少场景中物体的个数，降低算法复杂度

消隐的分类

按消隐对象和输出结果分类

线消隐：消除的是物体上不可见的边。

面消隐：消除的是物体上不可见的面。

根据消隐空间分类

1️⃣ 物体空间的消隐算法：以场景中的物体为处理单元；

for (场景中的每一个物体)
{
	将其与场景中的其它物体比较，确定其表面的可见部分；
	显示该物体表面的可见部分；
}

假设场景中有k个物体，平均每个物体表面由h个多边形构成，显示区域中有m*n个像素，则算法的复杂度为：O((kh)*(kh))

2️⃣ 图像空间的消隐算法：以窗口内的每个像素为处理单元；

for(窗口内的每一个像素)
{
 确定距视点最近的物体，以该物体表面的颜色来显示像素
}

假设场景中有k个物体，平均每个物体表面由h个多边形构成，显示区域中有m*n个像素，则算法的复杂度为：O(mnkh)

•实际应用中通常会考虑画面的连贯性，所以图像空间算法的效率有可能更高。

3️⃣ 物体空间和图像空间的消隐算法：在物体空间中预先计算面的可见性优先级，再在图像空间中生成消隐图；

代表性算法：画家算法

消除隐藏线

对造型的要求

在线框表示模型中，要求造型系统中有面的信息，最好有体的信息。

坐标变换

通过坐标变换，将视点变换到Z轴的正无穷大处，视线方向变为Z轴的负方向。

最基本的运算

线消隐中，判断面对线的遮挡关系：体分解成面，再判断面与线关系。判断过程中需反复地进行线线、线面之间的求交运算。

算法

1️⃣ 若线段的两端点及视点在给定平面的同侧，线段不被给定平面遮挡，转(7)；

2️⃣ 若线段的投影与平面投影的包围盒无交，线段不被给定平面遮挡，转(7)；

3️⃣ 求直线与相应无穷平面的交：

•无交点转(4)；

•若交点在线段内部，交点将线段分成两段，与视点同侧一段不被遮挡，另一段在视点异侧转(4)；

•若交点在线段外部,转(4)。

4️⃣ 求所剩线段的投影与平面边界投影的所有交点。若无交点，转(7)。

5️⃣ 以上所求得的各交点将线段的投影分成若干段，求出第一段中点。

6️⃣ 若第一段中点在平面的投影内，则相应的段被遮挡，否则不被遮挡；其他段的遮挡关系可依次交替取值进行判断。

7️⃣ 结束。

假设E为面F的一条边, 需判别F以外每一个面与E的遮挡关系。

假设消隐对象有n条边和m个面，当n和m很大时，两两求交的消隐方法工作量很大：

解决方法：背面剔除。

消除隐藏面（不太好出考题）

画家算法

列表优先算法：画家的作画顺序暗示出所画物体之间的相互遮挡关系。

基本思想

1️⃣ 先把屏幕置成背景色；

2️⃣ 再把物体的各个面按其离视点的远近进行排序，排序结果存在一张深度优先级表中；

3️⃣ 然后按照从远到近的顺序逐个绘制各个面。

关键是如何对场景中的物体按深度排序。

多边形排序算法

在规范投影坐标系里 XYZ 中，投影方向是 Z轴的负方向，因而 Z坐标大者距观察者更近。Zmin(P)和 Zmax(P) 分别为 P 各顶点 Z坐标的最小和最大值。[投影为正平行投影]

Step 1:将场景中所有多边形存入一个线性表，记为L；

Step 2:如果L中仅有一个多边形，算法结束；否则根据每个多边形的Zmin对它们预排序。不妨假定多边形P落在表首，即Zmin§为最小。再记Q为L–{P}(表中其余多边形）中任意一个；

Step 3:判别P, Q之间的关系，有如下二种：

对所有的Q，有Zmax§< Zmin(Q), 则多边形P的确距观察点最远，它不可能遮挡别的多边形。令L=L–{P}, 返回第二步；

存在某一个多边形Q，使Zmax§>Zmin(Q),需进一步判别：

优点：简单（如何对场景中的物体按深度排序）。

缺点：只能处理互不相交的面，且深度优先级表中面的顺序可能出错

Z缓冲区算法

组成

帧缓冲器–保存各像素颜色值；

Z 缓冲器 –保存各像素处物体深度值；

Z缓冲器中的单元与帧缓冲器中的单元一一对应

算法思想

1️⃣ 将 Z 缓冲器中个单元的初始值置为最小值。

2️⃣ 多边形投影时，当要改变某个像素的颜色值时，首先检查当前多边形的深度值是否大于该像素原来的深度值：

大于，说明当前多边形更靠近观察点，用它的颜色替换像素原来的颜色；同时更新深度值；

否则说明在当前像素处，当前多边形被前面所绘制的多边形遮挡了，是不可见的，像素的颜色值不改变。

Z-Buffer算法（）
{ 	
	帧缓存全置为背景色
	深度缓存全置为最小Z值
	for(每一个多边形)
	{   
		扫描转换该多边形
	    for(该多边形所覆盖的每个象素(x,y) )
	   {	
	   		计算该多边形在该象素的深度值Z(x,y);
			if(Z(x,y)大于Z缓存在(x,y)的值)
			{    
				把Z(x,y)存入Z缓存中(x,y)处
				把多边形在(x,y)处的颜色值存入帧缓存的(x,y)处
			}	
	  }                       
     }                                                
}

需要计算的像素深度值次数 =多边形个数*多边形平均占据的像素个数

所有图像空间算法中最简单的一种隐藏面消除算法

优点：

简单稳定，利于硬件实现；

不需要整个场景的几何数据。

缺点:

空间：需要一个额外的Z缓冲器；

时间：在每个多边形占据的每个像素处都要计算深度值。

只用一个深度缓存变量zb的改进算法：需要开一个与图象大小相等的缓存数组ZB

{
	帧缓存全置为背景色
	for (屏幕上的每个象素(i, j)) {
		深度缓存变量zb置最小值MinValue
		for (多面体上的每个多边形Pk) {
			if (象素点(i, j)在Pk的投影多边形之内) {
				计算Pk在(i, j)处的深度值depth;
				if (depth大于zb) {
					zb = depth;
					indexp = k;
				}
			}
		}
		if (zb != MinValue)
			在交点 (i, j) 处用多边形Pindexp的颜色显示
		}
}

先像素后多边形

关键问题

1️⃣ 计算多边形在点（i，j）处的深度。设多边形的平面方程为：

2️⃣ 判断象素点(i,j)是否在的投影多边形之内（点与多边形的包含性检测）

射线法

由被测点P处向 y = – ¥方向作射线

交点个数是奇数，则被测点在多边形内部；

否则，偶数，在多边形外部；

若射线正好经过多边形的顶点，则采用“左开右闭”的原则来实现。

弧长法（单位圆）

–以被测点为圆心作单位圆，计算其在单位圆上弧长的代数和

代数和为0，点在多边形外部；

代数和为

2

π

2\\pi

$2 π$ ，点在多边形内部；

代数和为

π

\\pi

$π$ ，点在多边形边上。

弧长累加方法：以顶点符号为基础。

将坐标原点移到被测点P。各象限内点的符号对分别为(＋,＋)，（－，＋)，(－，－)，(＋，－)。

算法规定：若顶点pi的某个坐标为0,则其符号为＋。若顶点pi的x、y坐标都为0，则说明这个顶点为被测点，我们在这之前予以排除。于是弧长变化如下表。

注意：当边的终点Pi+1在起点Pi的相对象限时，弧长变化可能增加或减少p：

扫描线Z-buffer算法[了解就行]

Z 缓冲器算法中所需要的Z 缓冲器容量较大，可以将整个绘图区域分割成若干个小区域，然后一个区域一个区域地显示，以减少Z 缓冲器的单元数；

如果将小区域取成屏幕上的扫描线，就得到扫描线 Z 缓冲器算法。

算法思想

1️⃣ 面Buffer到线Buffer；

2️⃣ 利用图形的连贯性(指深度计算)；

3️⃣ 在处理当前扫描线时，开个一维数组作为当前扫描线的Z-buffer。找出与当前扫描线相关的多边形，以及每个多边形中相关的边对；

4️⃣ 对每一个边对之间的小区间上的各象素，计算深度，并与Z-buffer中的值比较，找出各象素处可见平面；

5️⃣ 确定颜色，写帧缓存：采用增量算法计算深度。

改进

1️⃣ 将窗口分割成扫描线：Z缓冲器的单元数只要等于一条扫描线内像素的个数就可以了。

2️⃣ 采用多边形Y(分类)表、活化多边形表避免多边形与扫描线的盲目求交；

3️⃣ 利用边、边的分类表、边对、活化边对表避免边与扫描线的盲目求交。

4️⃣ 利用连贯性计算深度

水平方向：当沿扫描线x递增一个像素时，多边形所在平面在z坐标的增量，对方程ax+by+cz+d=0来说，

−

\\Delta z_a=-a/c

$Δ z_{a} = - a / c$

竖直方向

\\Delta z_b

$Δ z_{b}$ ：当沿扫描线y递增一个像素时，多边形所在平面 z坐标的增量，

−

\\Delta z_b=-b/c

$Δ z_{b} = - b / c$

下一条扫描线与边对左侧边交点处的深度值：

z_1=z_1+\\Delta x_1 \\Delta z_a+\\Delta z_b

$z_{1} = z_{1} + Δ x_{1} Δ z_{a} + Δ z_{b}$

数据结构

多边形Y表；活化多边形表(APT);边表(ET);活化边对表(AET)。

多边形Y表

存放所有多边形信息。

根据多边形顶点中最小的y坐标，插入多边形Y表中的相应位置；

根据序号可从定义多边形的数据结构中取多边形信息。(ax+by+cz+d=0的系数，多边形的边，顶点坐标和颜色

活化多边形表APT：与当前扫描线相交的多边形。

APT是一个动态的链表。

边表ET：活化多边形表中的每一个多边形都有一个边表ET(每条边端点中较大者，增量 Dx，y值较小一端的x坐标和z坐标)

活化边对表AET

在一条扫描线上，同一多边形的相邻两条边构成一个边对。活化边表AET中存放当前多边形中与当前扫描线相交的各边对的信息。

扫描线Z - buffer算法() {
	建多边形y表；根据多边形顶点最小y值，将多边形置入多边形y表。
	活化多边形表APT，活化边对表AET初始化为空。
	For(每条扫描线i，i从小到大) {
		1. 帧缓存CB置为背景色。
		2. 深度缓存ZB (一维数组) 置为负无穷大。
		3. 将对应扫描线i的，多边形Y表中的多边形加入到活化多边形表APT中。
		4. 对新加入的多边形，生成其相应的边表。
		5. 对APT中每一个多边形，若其边表中对应扫描线i增加了新的边，将新的边配对，加到活化边对表AET中。
		6. 对AET中的每一对边：
			6.1 对xl < j < xr 的每一个象素，按增量公式z = z + ? za计算各点depth 。
		    6.2 与ZB中的量比较，depth > ZB(j), 则令ZB(j) = depth，并确定颜色
		                值，写帧缓存。
		7. 删除APT中多边形顶点最大y坐标为i的多边形，并删除相应的边。
		8. 对AET中的每一个边对，作如下处理：
		    8.1 删除ylmax或yrmax 已等于i的边。若一边对中只删除了其中一边，
		        对该多边形的边重新配对。
		    8.2 用增量公式计算新的xl 、 xr 和zl
	}
}

缺点

在每一个被多边形覆盖像素处需要计算深度值；

被多个多边形覆盖的像素需要多次计算深度值。

对比

与Z-Buffer算法相比，扫描线算法有了很大改进

优点：

将整个绘图窗口内的消隐问题分解到一条条扫描线上解决，使所需的Z-Buffer大大减少；

计算深度值时，利用了面连贯性，只用了一个加法。

缺点：

每个像素处都计算深度值，甚至不止一次的计算（多边形重叠区域），运算量仍然很大。

改进

在一条扫描线上，每个区间只计算一次深度，即区间扫描线算法，又称扫描线算法

区间扫描线算法

基本思想

把当前扫描线与各多边形在投影平面的投影的交点进行排序后，使扫描线分为若干子区间。只要在区间任一点处找出在该处z值最大的一个面，这个区间上的每一个象素就用这个面的颜色来显示。

注意：该算法要求多边形不能相互贯穿，否则在同一区间上，多边形深度值的次序会发生变化。

如何确定小区间的颜色可分为三种情况

小区间上没有任何多边形，如[a4,a5]，这时该小区间用背景色显示；

小区间上只有一个多边形，如[a1,a2][a5,a6]这时可以对应多边形在该处的颜色显示；

小区间上存在两个或两个以上的多边,形如[a6,a7]，必须通过深度测试判断哪个多边形可见。

若允许物体表面相互贯穿时，还必须求出它们在扫描平面的交点。用这些交点把该小区间分成更小的子区间，在这些间隔上决定哪个多边形可见。如将[a2,a3]区间分成[a2,b][b,a3]两个子区间

类似于扫描线Z-Buffer算法中的数据结构

多边形分类表、活化多边形表、边表、活化边表

活化边表中的结点是边，而非边对

❓ 如何知道每一个区间中，有几个相关的多边形？是哪几个？

🏷 解决方案：活化多边形表中增加一个标志，flag=0, 每遇到它的边，flag取反。

for (绘图窗口内的每一条扫描线）
{   求投影与当前扫描线相交的所有多边形
     求上述多边形中投影与当前扫描线相交的所有边，将它们记录在活化边表AEL中
     求AEL中每条边的投影与扫描线的交点；
     按交点的u坐标将AEL中各边从左到右排序，  两两配对组成一个区间；
      for （AEL中每个区间）
       {
          求覆盖该区间的所有多边形，将它们记入活化多边形表APL中；
          在区间上任取一点，计算APL中各多边形在该点的深度值，记深度最大者为P；
           用多边形P的颜色填充该区间
        }
}

算法的优点：将逐点(象素、Pixel)计算改为逐段计算,效率大大提高！

区域子分割算法

基本思想

首先将场景中的多边形投影到绘图窗口内，判断窗口是否足够简单，若是则算法结束；否则将窗口进一步分为四块。对此四个小窗口重复上述过程，直到窗口仅为一个像素大小。此时可能有多个多边形覆盖了该像素，计算它们的深度值，以最近的颜色显示该像素即可。

何谓窗口足够简单

窗口为空，即多边形与窗口的关系是分离的；

窗口内仅含一个多边形，即有一个多边形与窗口的关系是包含或相交。此时先对多边形投影进行裁剪，再对裁剪结果进行填充；

有一个多边形的投影包围了窗口，并且它是最靠近观察点的，以该多边形颜色填充窗口。

•分离和包围多边形的判别方法：射线检查法；转角累计检查法；区域检查法（考试不考）

光线投射算法

基本思想：

1️⃣ 考察由视点出发穿过观察屏幕一象素而射入场景的一条射线，则可确定出场景中与该射线相交的物体；

2️⃣ 在计算出光线与物体表面的交点之后，离象素最近的交点的所在面片的颜色为该象素的颜色；

3️⃣ 如果没有交点，说明没有多边形的投影覆盖此象素，用背景色显示它即可。

for屏幕上的每一象素
  {形成通过该屏幕象素(u,v)的射线；
	 for 场景中的每个物体
         {将射线与该物体求交；
		if 存在交点
		     以最近的交点所属的颜色显示象素(u,v)
		 else
		      以背景色显示象素(u,v)
	    }
    }

光线投射算法与Z缓冲器算法相比，它们仅仅是内外循环颠倒了一下顺序，算法复杂度类似