第22.7节性能篇-使用八叉树结构来管理场景-卡核

天下武功，唯快不破

最近网友问了关于点云、倾斜摄影数据的性能优化问题。本来想刀枪剑戟、斧钺勾叉给弄了，但是后来想性能其实是个系统问题，要在第22节分成数小节扎扎实实的讲一讲。

鸣谢

非常感谢王锐王大神的cookbook，我准备主要参考它里面关于性能的一章。也就是第8章。

本节资源

本文集包括本节所有资源包括模型代码都在此下载，按节的序号有文件或文件夹：

问题描述

我们为什么使用googlEarth或者osgEarth的时候，原则上可以加载无限大的数据呢，其原因就是因为其使用的是树状的组织结构，如下：
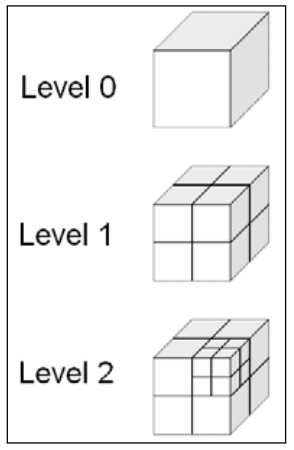
在这里插入图片描述
我们仍然来拿地球来想象，Level0是最粗的球，我们离的很远的时候是这个球。Level1是我们拉近一点，地球会一分为八，然后我们再对着其中一个角拉近就分裂成Level2的模样，这个角又一分为八。

粗的级别就显示粗的内容，细的级别就加载细的内容，就像高清影像的瓦片一样，第0级可以是整个地球，分辨率是256X256，然后一分为八，每张图片的范围变成了第0级的八分之一，但是分辨率仍然是256×256，就越往下拉越清晰。

本节我们就来构建这样一个八叉树的结构，本节如果你搞明白了，就入门了八叉树的结构，因为在构建树状结构的时候往往会用到递归。理解起来还是有点费劲的。LOD和PagedLOD都大量的用作构建数字地球等，其实原理都和本节差不多。

本节功能

1、随机生成5000个球，坐标范围在[-500, 500]。
2、对这5000个球生成八叉树，其结束条件是这样的：当结点的孩子小于16个时认为是叶结点，就不再往下分了。或者树的深度大于32也不往下分了。3、每一层我们用一个LOD来保存，当离的很远时显示父亲（把包围盒绘制出来），当拉近时父亲就一分为八。直到显示叶结点。

听起来就晕了吧，一定要好好的缕一缕。
在这里插入图片描述

具体实现

1、随机生成小球没有什么好说的。我们将生成的所有的小球的包围盒都压在globalElements当中，将所有小球组成的最大包围盒记为globalBound

    typedef std::pair<std::string, osg::BoundingBox> ElementInfo;
    osg::BoundingBox globalBound;
    std::vector<OctreeBuilder::ElementInfo> globalElements;
    for ( unsigned int i=0; i<5000; ++i )
    {
        osg::Vec3 pos = randomVector( -500.0f, 500.0f );
        float radius = randomValue( 0.5f, 2.0f );
        std::stringstream ss; ss << "Ball-" << i+1;
        
        osg::Vec3 min = pos - osg::Vec3(radius, radius, radius);
        osg::Vec3 max = pos + osg::Vec3(radius, radius, radius);
        osg::BoundingBox region(min, max);
        globalBound.expandBy( region );
        globalElements.push_back( OctreeBuilder::ElementInfo(ss.str(), region) );
    }

2.2、然后我们直接就开始调用OctreeBuilder的build方法开始构建八叉树：

    OctreeBuilder octree;
    osg::ref_ptr<osg::Group> root = octree.build( 0, globalBound, globalElements );

2.3、build是个递归方法，有三个参数，第一个是当前级别，第二个是当前包围盒，第三个是当前元素，其中主要干了以下几件事：
a) 先把当前包围盒的最大点、中间点、最小点给记录下来到extentSet中，以便以这三个数为界一分为八：

    //存放当前包围盒的最大、中间、最小点，以为划分八叉树做准备
    osg::Vec3 extentSet[3] = {
        total._min,
        (total._max + total._min) * 0.5f,
        total._max
    };

b) 把当前元素每个都判断一下是不是在当前盒子中，有人说了build(0,…)的时候那不废话吗，肯定都在盒子里了。但是build(1,…)的时候就不一定了。这一步是要判断传入的元素（往往是父结点的所有元素）是不是在当前盒子（子结点的盒子里），因此要进行判断：

    std::vector<ElementInfo> childData;
    //遍历父结点的所有孩子，让包含在当前盒子里的，不完全包含但是中点在盒子里的，都压入到
    //当前盒子的子结点
    for ( unsigned int i=0; i<elements.size(); ++i )
    {
        const ElementInfo& obj = elements[i];
        if ( total.contains(obj.second._min) && total.contains(obj.second._max) )
            childData.push_back( obj );
        else if ( total.intersects(obj.second) )
        {
            osg::Vec3 center = (obj.second._max + obj.second._min) * 0.5f;
            if ( total.contains(center) ) childData.push_back( obj );
        }
    }

c) 判断完成之后，要看看当前盒子里的元素数量和级别，以此来判断当前盒子是不是叶结点

    //如果当前结点的孩子数量已经达标，或者层数已经达标，则认为
    //是叶结点
    bool isLeafNode = false;
    if ( (int)childData.size()<=_maxChildNumber || depth>_maxTreeDepth )
        isLeafNode = true;

d) 如果不是叶结点，就继续再一分为八，这个时候就把a)里面存的数字extentSet，拿它来将空间分成八个盒子：

        osg::ref_ptr<osg::Group> childNodes[8];

        //空间一分为八2*2*2
        for ( s[0]=0; s[0]<2; ++s[0] ) //x
        {
            for ( s[1]=0; s[1]<2; ++s[1] ) //y
            {
                for ( s[2]=0; s[2]<2; ++s[2] ) //z
                {
                    // Calculate the child extent
                    //extentSet 0是最小，1是中间，2是最大
                    //下面这个小算法有点磨人，分另求出min和max的x, y, z自己好好推几个试试
                    osg::Vec3 min, max;
                    for ( int a=0; a<3; ++a )
                    {
                        min[a] = (extentSet[s[a] + 0])[a];
                        max[a] = (extentSet[s[a] + 1])[a];
                    }
                    
                    //这么求id是为了确保唯一性
                    int id = s[0] + (2 * s[1]) + (4 * s[2]);
                    childNodes[id] = build( depth+1, osg::BoundingBox(min, max), childData );
                }
            }
        }

e) 如果是叶结点，那就构建一个LOD，离的远时，拿其父的包围盒构建一个盒子，离的近的时候就显示叶结点（小球）。

   else //找到叶结点，递归就结束了
    {
        for ( unsigned int i=0; i<childData.size(); ++i )
        {
            const ElementInfo& obj = childData[i];
            osg::Vec3 center = (obj.second._max + obj.second._min) * 0.5;
            float radius = (obj.second._max - obj.second._min).length() * 0.5f;
            //创建一个球
            group->addChild( createElement(obj.first, center, radius) );
        }
    }
    
    osg::Vec3 center = (total._max + total._min) * 0.5;
    float radius = (total._max - total._min).length() * 0.5f;

    //最后创建一个LOD，离的远了显示调试盒子，离的近了显示分的组
    osg::LOD* level = createNewLevel( depth, center, radius );
    level->insertChild( 0, createBoxForDebug(total._max, total._min) );  // For debug use
    level->insertChild( 1, group.get() );
    return level;