精确HLR之边数据-卡核

Abstract. 精确HLR算法是根据模型生成图纸的重要算法，使用精确HLR算法，对于球体、圆柱体、圆锥体可以生成直线和圆弧，为生成的图纸再加工提供一些便利。OpenCASCADE中精确HLR算法较Poly算法要慢，但是功能可用，实现原理简单，主要是比较边和面的遮挡关系，还是有参考学习价值。本文主要关注精

确HLR算法中重要数据边的数据。

Key Words. HLR, Outline, Contour, Iso Line

1 Introduction

OpenCASCADE中总体上都在遵循程序Programs=数据结构Data Structure+算法Algorithms的原则。如功能模块命名上：ModelingData, ModelingAlgorithms，布尔算法中的Package命名BOPDS, BOPAlgo，再到精确HLR算法中的类也是这样来命名：HLRBRep_Data, HLRBRep_Algo。编写程序时，先设计好输入输出的数据结构，再以此为基础构筑相关算法，从而实现一定的程序功能。HLR算法的实现原理在文档中由一句话描述：Comparing each edge of the shape to be visualized with each of its faces, and calculating the visible and hidden parts of each edge. 用每条边去和每个面判断遮挡关系，计算出边的可见和隐藏部分。在精确HLR的数据结构HLRBRep_Data中主要就是存储边HLRBRep_EdgeData和面HLRBRep_FaceData的数据。本文通过将边的数据可视化出来，分析HLRBRep_Data中的数据。

2 HLR边的分类

OpenCASCADE对于精确HLR算法中边主要分为三类：拓扑边Edge，轮廓线Outline和等参线Iso Line。其中拓扑边根据边的连续性又分为：Sharp Edge, Smooth Edge, Sewn Edge. 如下图所示为官方文档中关于边的分类说明：

对于轮廓线和等参线都需要有对应的算法来生成。对HLR算法中边的数据生成算法和数据结构都在package HLRTopoBRep中，其中生成轮廓线的算法类为HLRTopoBRep_OutLiner，生成等参线的算法类为HLRTopoBRep_FaceIsoLiner。所有数据都存储到HLRTopoBRep_Data中。这里有个定义：对于没有自交self-intersecting的线来说是简单曲线Simple Curve。

3 等参线

面上等参线Isoparameter是曲面的参数方程S(u, v)其中一个参数固定，另一个参数变化生成的曲线。对于Geom_Surface提供UIso()和VIso()函数来计算曲面上的等参线。当面上有孔洞时，如何得到正确的等参线是个需要思考的问题。等参线的计算使用类HLRTopoBRep_FaceIsoLiner，核心算法是使用Hatcher工具来进行计算，相关类的实现说明可以参考之前写的文章《Hatcher的使用》。

从目前一些商业软件的出图功能来看，给模型增加ISO线的需求较少，一般出图时不生成ISO线。

4 轮廓线

轮廓线是模型根据投影方向计算得到的线，计算轮廓线的功能实现在Contap中的类Contap_Contour。轮廓线是在指定的投影方向上曲面可见和不可见的分界线，即曲面上法向与投影方向垂直的点的连线。轮廓线的计算还考虑透视投影和平行投影。如果只指定一个视点，则按透视投影计算轮廓线。如果指定投影方向，则按平行投影计算轮廓线。通过HLRTopoBRep_OutLiner::Fill()函数来计算。

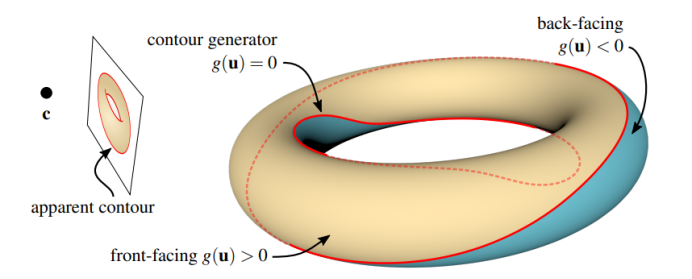对于球面、圆柱面和圆锥面，提供几何特例算法，使用类Contap_ContAna直接计算出轮廓线。若是其他曲面，则使用类Contap_SurfFunction建立轮廓线方程，并对其进行求解来计算轮廓线。轮廓线使用类Contap_Line表示，得到的轮廓线分为四类：

Contap_Lin：直线，如圆柱侧面投影会得到两条直线；
Contap_Circle：圆，如球面投影会得到圆；
Contap_Walking：一般曲面轮廓线，因为使用Walking(Marching Method)算法求解一般曲面的轮廓线二元函数方程，所以得到的是Walking线；
Contap_Restriction：边界线上的一部分。

从上述轮廓线类型可以看出，使用精确HLR算法，对于球面、圆柱面和圆锥面进行消隐，可以得到直线和圆这种精确表示。计算得到的轮廓线会结合面的参数定义域Domain对轮廓线进行裁剪，处理参数定义域的类是BRepTopAdaptor_Tool。

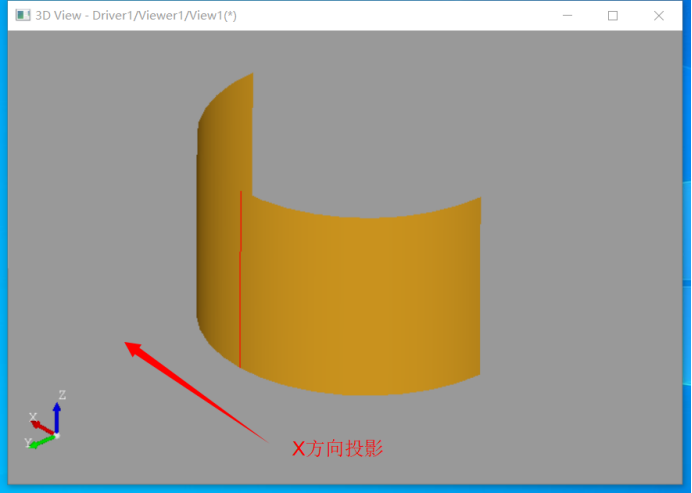如上图所示一半的圆柱面在X方向投影得到的轮廓线只有一条红色的直线。

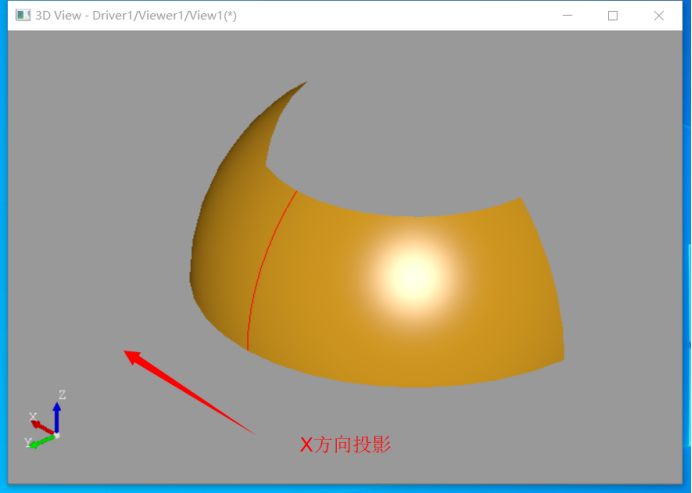如上图所示部分球面在X方向投影得到的轮廓线也是红色的圆弧，不是整圆。通过曲面的参数定义域，已经将所得到的轮廓线限制在参数定义域内。如果是Walking得到的轮廓线，返回是Marching过程中的一系列点，会对这些点进行拟合。对于轮廓线也分成两类，一种是内部轮廓线internal outline，一种是在边界上的轮廓线outline on restriction。

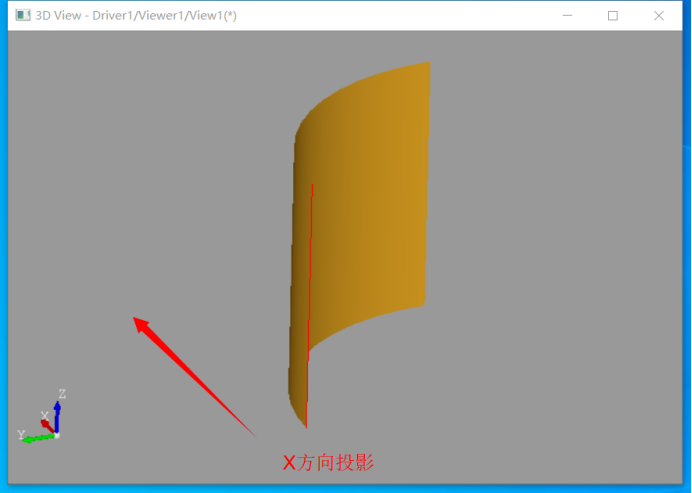当轮廓线在边界上的时候，返回的轮廓线类型为Restriction。如上图所示为四分之一圆柱面沿X方向投影得到的轮廓线为Restriction轮廓线。

5 Conclusion

OpenCASCADE中HLR算法的代码可读性较差，但是功能基本上是可用的，有参考学习价值。HLR算法相对布尔算法来说要简单，理解HLR算法为实现根据模型生成图纸的功能打下基础。HLR算法主要思路是来判断线与面的遮挡关系，线的数据来源除了EDGE以外，还有等参线和轮廓线。理解线的数据结构后，下一步来理解面的数据结构，从而能掌握HLR算法甚至对其进行改造。