1 Introduction
曲线上有一些特殊点会影响曲线的连续性,如重点(Multiple Point)、尖点(Cusp Point)、拐点(Inflection Point)等。一般称曲线上凸弧和凹弧的分界点称为拐点。
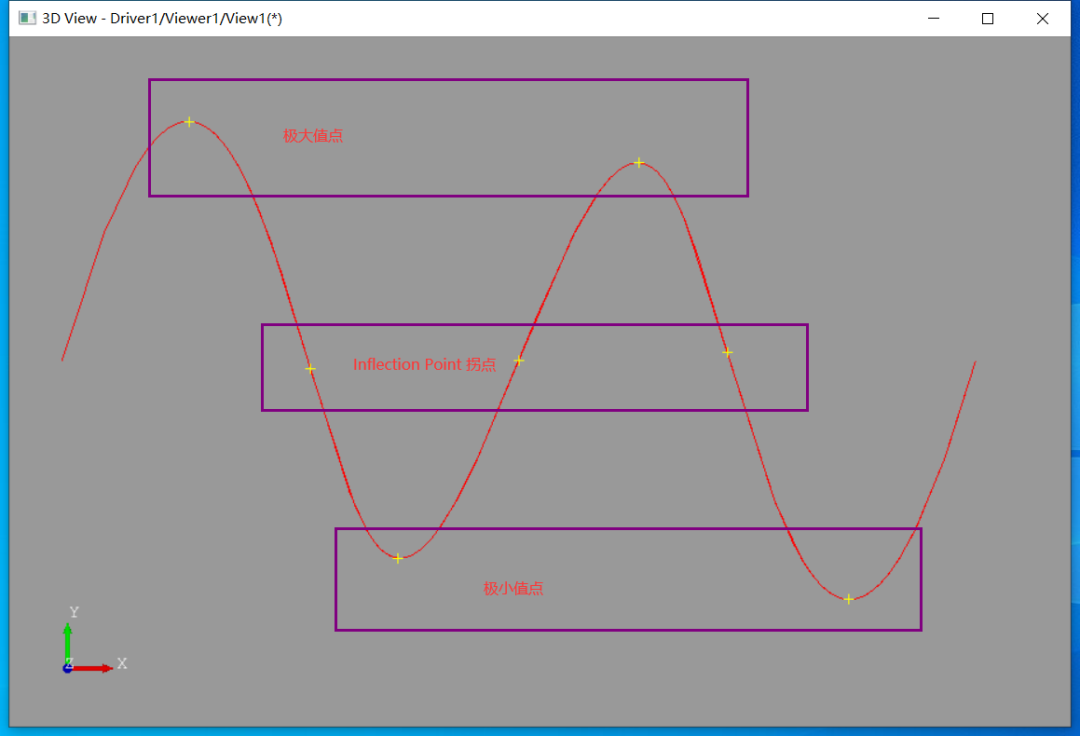
图1 曲线极值点和拐点
在高等数学中[1]给出了曲线拐点的定义及判别方法。曲线上的拐点数学定义很简单,一般的判断方法是计算曲线上二阶导为0处左右曲线两侧曲率的符号,若符号不同,则为拐点。但是给定任意一条曲线怎么用程序计算出拐点呢?
2 拐点 Inflection Point
OCCT中在包Geom2dLProp提供二维曲线局部属性分析功能,其中类Geom2dLProp_CurAndInf2d可以计算二维曲线的极值点Local extremas和拐点Inflection。这些点分以下三种类型:
//! Identifies the type of a particular point on a curve:
//! - LProp_Inflection: a point of inflection
//! - LProp_MinCur: a minimum of curvature
//! - LProp_MaxCur: a maximum of curvature.
enum LProp_CIType
{
LProp_Inflection,
LProp_MinCur,
LProp_MaxCur
};
其中计算拐点函数代码如下所示:
void Geom2dLProp_NumericCurInf2d::PerformInf(const Handle(Geom2d_Curve)& C,
const Standard_Real UMin,
const Standard_Real UMax,
LProp_CurAndInf& Result)
{
isDone = Standard_True;
Geom2dLProp_FuncCurNul F(C);
Standard_Real EpsX = 1.e-6;
Standard_Real EpsF = 1.e-6;
Standard_Integer NbSamples = 30;
math_FunctionRoots SolRoot (F,UMin,UMax,NbSamples,EpsX,EpsF,EpsX);
if (SolRoot.IsDone()) {
for (Standard_Integer j = 1; j Result.AddInflection(SolRoot.Value(j));
}
}
else {
isDone = Standard_False;
}
}
既然拐点是一个数学概念,那么就是通过数学的方式来计算。首先建立曲线拐点方程F,再使用类math_FunctionRoots对方程进行求解,从而得到拐点。其中关键是拐点方程Geom2dLProp_FuncCurNul的建立。因为方程需要计算一阶数,相关代码如下:
//======================================================================
//function : Values
// purpose : F = (V1^V2.Z)/||V1||*||V2||
//======================================================================
Standard_Boolean Geom2dLProp_FuncCurNul::Values (const Standard_Real X,
Standard_Real& F,
Standard_Real& D)
{
gp_Pnt2d P1;
gp_Vec2d V1,V2,V3;
Geom2dLProp_Curve2dTool::D3(theCurve,X,P1,V1,V2,V3);
Standard_Real CP1 = V1.Crossed(V2);
Standard_Real CP2 = V1.Crossed(V3);
Standard_Real V1V2 = V1.Dot(V2);
Standard_Real V2V3 = V2.Dot(V3);
Standard_Real NV1 = V1.Magnitude();
Standard_Real NV2 = V2.Magnitude();
F = 0. ;
D = 0. ;
/*
if (Abs(CP1) return Standard_True;
} else */
if (NV2 1.e-4) {
return Standard_True;
} else if (NV1*NV2 return Standard_False;
} else {
F = CP1/(NV1*NV2);
D = (CP2 - CP1*V1V2/(NV1*NV1) - CP1*V2V3/(NV2*NV2))/(NV1*NV2);
}
return Standard_True;
}
根据参数曲线曲率计算公式:
曲线拐点出现在曲率k消失为0的地方,如下图所示:
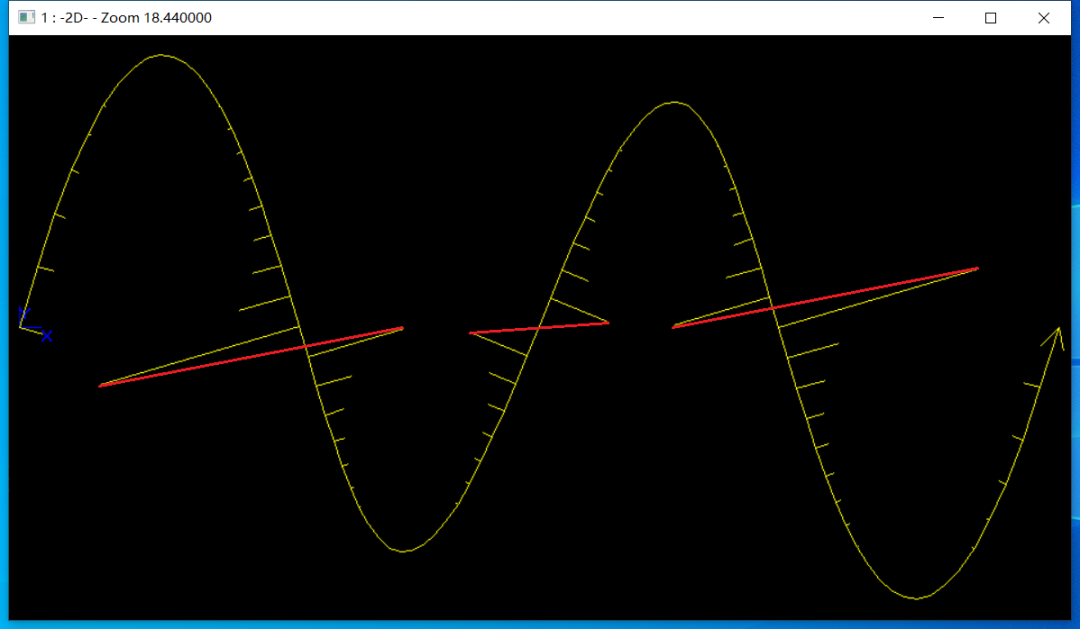
由于在给定参数区域曲线正则,所以存在一阶可导,即曲率计算公式中分母不为0。所以可以使用一阶导和二阶导的叉乘来建立方程:。根据注释和源码,类Geom2dLProp_FuncCurNul建立的二维参数曲线拐点方程计算公式为:
根据函数的和、差、商和积求导法则及复合函数求导法则,二维参数曲线拐点方程的一阶导计算公式为:
请同学们根据程序代码自己推导一下,看看了一阶导公式是否正确。
3 Conclusion
综上所述,对于数学上显示易见的的一些概念如果要实现程序来检测,还不是那么容易的。OCCT中提供了二维参数曲线的极值点和拐点检测功能。作为练习,可以思考一下尖点和极值点怎么判别?
4 参考文献
[1] 同济大学数学系. 高等数学. 高等教育出版社. 2014
[2] Dinesh Manocha, John F. Canny. Detecting Cusps and Inflection Points in Curves. Computer Aided Geometric Design. 1992
[3] Yong-Ming Li, Robert J. Cripps. Identification of inflection points and cusps on rational curves. Computer Aided Geometric Design. 1997


![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)










暂无评论内容