OpenCASCADE Shape Location-卡核

OpenCASCADE Shape Location

Abstract. The TopLoc package of OpenCASCADE gives resources to handle 3D local coordinate systems called Locations. A Location is a composition of elementary coordinate systems, each one is called a Datum. The Location keeps track of this composition. The paper will use the Draw Test Harness to illustrate the Location concept.

Key Words. Transformation, Location, Local Coordinate Systems

1.Introduction

对于三维空间中的各种模型，总是想要摆放到合适的位置，最终形成一个工厂的模型，一艘船的模型，一个建筑物的模型，等等。目前来看，所有的几何相关的库对模型变换的实现一般都是使用了矩阵变换。有的可能只保留了最终变换的结果矩阵数据，而OpenCASCADE的TopoDS_Shape中保留了Location信息。从其文档可以看出，Location中保留了模型变换一系列的变换组合，并可以对这个变换进行Track追踪。如何来正确理解这个Location的意义呢？下面结合Draw Test Harness来进行说明。

2.Draw Test

在Draw Test Harness中对模型进行变换的命令有：ttranslate, trotate, tmove, reset, tmirror, tscale.其中ttranslate, trotate, tmove, reset命令只会对模型位置进行调整，并不能让模型发生变形，即是刚性变换。下面就通过对一个Box进行移动和旋转，来看看TopoDS_Shape中的Location是如何变化的。在Draw Test Harness中输入以下命令：

pload ALL 
box b 10 20 30 
vdisplay b 
vtrihedron vt 
dump b

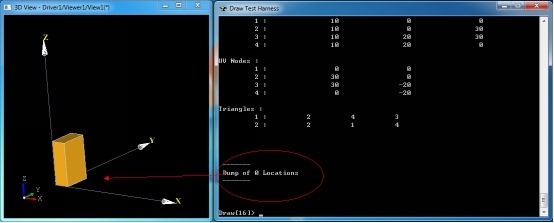
可以看到此时box的Location是没有的：

Figure 2.1 Box Location in Original

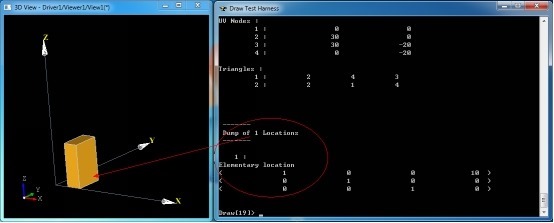
当将box沿X方向移动一段距离后：

# translate by x direction 
ttranslate b 10 0 0 
vdisplay b 
dump b

Figure 2.2 Location of the translation box

由上图可知，当对模型进行变换后，TopoDS_Shape中即有了Location数据，变换矩阵的平移部分（第4列数据）发生了变化。下面继续沿X轴方向移动10：

# translate by x direction 
ttranslate b 10 0 0 
vdisplay b 
dump b

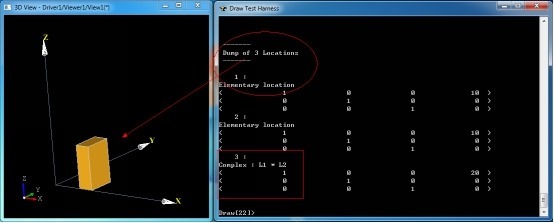
Figure 2.3 Translate Box in X Direction

由图2.3可知，模型现在的位置是通过两个Elementary变换得来的。最后一个Complex变换是上述所有变换的复合。下面再对模型进行绕Y轴旋转45度：

# rotate by y axis 
trotate b 0 0 0 0 1 0 45 
vdisplay b 
dump b

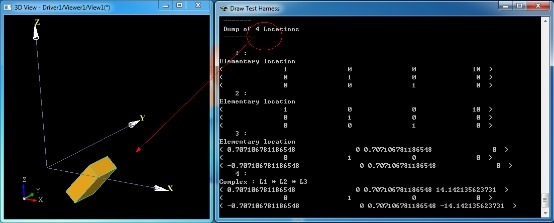
Figure 2.4 Rotate the Box

由上图可知，经过旋转变换后的模型有了4个Location：三个基本变换和一个复合变换，复合变换是所有基本变换的组合。

通过上面的示例，已经可以清晰理解OpenCASCADE中的Location的概念，虽然处理得有点复杂，通过Location可以对模型的变换轨迹有个详细的跟踪。这样处理的好处就是对模型的变换过程进行了记录，可以方便地回到历史上的任意一个时刻；不好的地方就是程序理解起来麻烦，而且还需要有额外的内存来保存这些数据。
以下为上述所有Tcl脚本：

#
# test TopoDS_Shape location.
# Shing Liu(eryar@163.com)
# 2016-09-06 22:50
# 

pload ALL

# initialize 
box b 10 20 30
vdisplay b
vtrihedron vt
dump b

# translate by x direction
ttranslate b 10 0 0
vdisplay b
dump b

# translate by x direction
ttranslate b 10 0 0
vdisplay b
dump b

# rotate by y axis
trotate b 0 0 0 0 1 0 45
vdisplay b
dump b

3.Draw Code

每个Draw Test Harness命令都可以方便地找到其实现代码，其中模型变换命令的实现代码如下：

//=======================================================================
// transform
//=======================================================================

static Standard_Integer transform(Draw_Interpretor& ,Standard_Integer n,const char** a)
{
  if (n <= 1) return 1;

  gp_Trsf T;
  Standard_Integer last = n;
  const char* aName = a[0];

  Standard_Boolean isBasic = Standard_False;

  if (!strcmp(aName,\"reset\")) {
  }
  else {
    isBasic = (aName[0] == \'b\');
    aName++;

    if (!strcmp(aName,\"move\")) {
      if (n < 3) return 1;
      TopoDS_Shape SL = DBRep::Get(a[n-1]);
      if (SL.IsNull()) return 0;
      T = SL.Location().Transformation();
      last = n-1;
    }
    else if (!strcmp(aName,\"translate\")) {
      if (n < 5) return 1;
      T.SetTranslation(gp_Vec(Draw::Atof(a[n-3]),Draw::Atof(a[n-2]),Draw::Atof(a[n-1])));
      last = n-3;
    }
    else if (!strcmp(aName,\"rotate\")) {
      if (n < 9) return 1;
      T.SetRotation(gp_Ax1(gp_Pnt(Draw::Atof(a[n-7]),Draw::Atof(a[n-6]),Draw::Atof(a[n-5])),
                    gp_Vec(Draw::Atof(a[n-4]),Draw::Atof(a[n-3]),Draw::Atof(a[n-2]))),
                    Draw::Atof(a[n-1])* (M_PI / 180.0));
      last = n-7;
    }
    else if (!strcmp(aName,\"mirror\")) {
      if (n < 8) return 1;
      T.SetMirror(gp_Ax2(gp_Pnt(Draw::Atof(a[n-6]),Draw::Atof(a[n-5]),Draw::Atof(a[n-4])),
                  gp_Vec(Draw::Atof(a[n-3]),Draw::Atof(a[n-2]),Draw::Atof(a[n-1]))));
      last = n-6;
    }
    else if (!strcmp(aName,\"scale\")) {
      if (n < 6) return 1;
      T.SetScale(gp_Pnt(Draw::Atof(a[n-4]),Draw::Atof(a[n-3]),Draw::Atof(a[n-2])),Draw::Atof(a[n-1]));
      last = n-4;
    }
  }

  if (T.Form() == gp_Identity || isBasic) {
    TopLoc_Location L(T);
    for (Standard_Integer i = 1; i < last; i++) {
      TopoDS_Shape S = DBRep::Get(a[i]);
      if (S.IsNull())
      {
        std::cerr << \"Error: \" << a[i] << \" is not a valid shape\\n\";
        return 1;
      }
      else
        DBRep::Set(a[i],S.Located(L));
    }
  }
  else {
    BRepBuilderAPI_Transform trf(T);
    for (Standard_Integer i = 1; i < last; i++) {
      TopoDS_Shape S = DBRep::Get(a[i]);
      if (S.IsNull()) {
        std::cerr << \"Error: \" << a[i] << \" is not a valid shape\\n\";
        return 1;
      }
      else {
        trf.Perform(S);
        if (!trf.IsDone())
          return 1;
        DBRep::Set(a[i],trf.Shape());
      }
    }
  }
  return 0;
}