OpenCASCADE Trihedron Law
Abstract. In differential geometry the Frenet-Serret formulas describe the kinematic properties of a particle moving along a continuous, differentiable curve in 3d space, or the geometric properties of the curve itself irrespective of any motion. More specifically, the formulas describe the derivatives of the so-called Tangent, Normal and Binormal unit vectors in terms of each other.
Key Words. Frenet-Serret Frame, TNB frame, Trihedron Law
1. Introduction
参数曲线上的局部坐标系,也称为标架Frame,OpenCASCADE中叫Trihedron。这个局部坐标系随着曲线上点的运动而运动,所以也称为活动坐标系。活动坐标系中各坐标轴的选取:
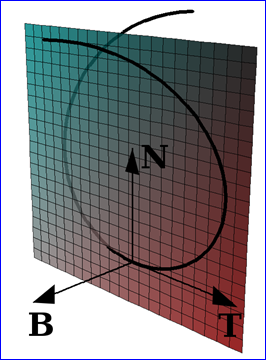
l T是参数曲线的切线方向;
l N是曲线的主法线方向,或称主法矢;主法矢总是指向曲线凹入的方向;
l B是副法矢;当T 和N确定后,通过叉乘即得到B。
Figure 1. T, N, B frame of a curve (from wiki)
定义一个活动标架有什么作用呢?把这个问题先保留一下。本文先介绍OpenCASCADE中的标架规则Trihedron Law。
2.Trihedron Law
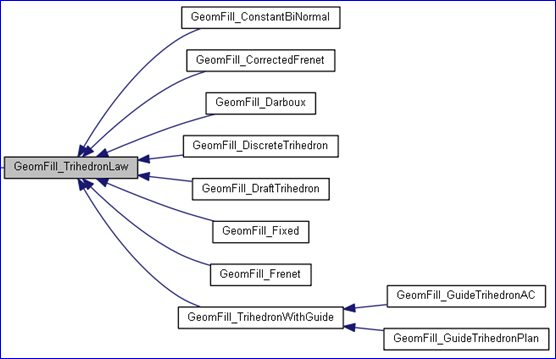
在OpenCASCADE中,类GeomFill_TrihedronLaw定义了曲线活动标架。其类图如下所示:
Figure 2. Trihedron Law define Trihedron along a Curve
从基类GeomFill_TrihedronLaw派生出了各种标架,如:
l GeomFill_Fixed:固定的活动动标架,即标架沿着曲线移动时,标架的三个方向是固定的;
l GeomFill_Frenet: Frenet标架;
l GeomFill_Darboux :Darboux标架;
l GeomFill_ConstantBiNormal:副法矢固定的标架;
3. Code Demo
下面通过示例代码来显示出曲线上的Frenet标架,GeomFill_TrihedronLaw子类的用法类似。
/* Copyright(C) 2018 Shing Liu(eryar@163.com) Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files(the \"Software\"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and / or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions : The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software. THE SOFTWARE IS PROVIDED \"AS IS\", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT.IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE. */ #include <TColgp_Array1OfPnt.hxx> #include <math_BullardGenerator.hxx> #include <GCPnts_UniformAbscissa.hxx> #include <GCPnts_UniformDeflection.hxx> #include <GCPnts_TangentialDeflection.hxx> #include <GCPnts_QuasiUniformDeflection.hxx> #include <Geom_BSplineCurve.hxx> #include <GeomAdaptor_HCurve.hxx> #include <GeomAPI_PointsToBSpline.hxx> #include <GeomFill_Fixed.hxx> #include <GeomFill_Frenet.hxx> #include <GeomFill_ConstantBiNormal.hxx> #include <GeomFill_CorrectedFrenet.hxx> #include <GeomFill_Darboux.hxx> #include <GeomFill_DiscreteTrihedron.hxx> #include <GeomFill_GuideTrihedronAC.hxx> #include <GeomFill_GuideTrihedronPlan.hxx> #include <BRepBuilderAPI_MakeEdge.hxx> #include <BRepTools.hxx> #pragma comment(lib, \"TKernel.lib\") #pragma comment(lib, \"TKMath.lib\") #pragma comment(lib, \"TKG2d.lib\") #pragma comment(lib, \"TKG3d.lib\") #pragma comment(lib, \"TKGeomBase.lib\") #pragma comment(lib, \"TKGeomAlgo.lib\") #pragma comment(lib, \"TKBRep.lib\") #pragma comment(lib, \"TKTopAlgo.lib\") void test() { TColgp_Array1OfPnt aPoints(1, 6); math_BullardGenerator aBullardGenerator; for (Standard_Integer i = aPoints.Lower(); i <= aPoints.Upper(); ++i) { Standard_Real aX = aBullardGenerator.NextReal() * 50.0; Standard_Real aY = aBullardGenerator.NextReal() * 50.0; Standard_Real aZ = aBullardGenerator.NextReal() * 50.0; aPoints.SetValue(i, gp_Pnt(aX, aY, aZ)); } GeomAPI_PointsToBSpline aBSplineFitter(aPoints); if (!aBSplineFitter.IsDone()) { return; } std::ofstream aTclFile(\"d:/tcl/trihedron.tcl\"); aTclFile << std::fixed; aTclFile << \"vclear\" << std::endl; Handle(Geom_BSplineCurve) aBSplineCurve = aBSplineFitter.Curve(); Handle(GeomAdaptor_HCurve) aCurveAdaptor = new GeomAdaptor_HCurve(aBSplineCurve); BRepBuilderAPI_MakeEdge anEdgeMaker(aBSplineCurve); BRepTools::Write(anEdgeMaker, \"d:/edge.brep\"); aTclFile << \"restore \" << \" d:/edge.brep e\" << std::endl; aTclFile << \"incmesh e \" << \" 0.01\" << std::endl; aTclFile << \"vdisplay e \" << std::endl; Handle(GeomFill_Frenet) aFrenet = new GeomFill_Frenet(); aFrenet->SetCurve(aCurveAdaptor); GCPnts_UniformAbscissa aPointSampler(aCurveAdaptor->Curve(), 5.0); for (Standard_Integer i = 1; i <= aPointSampler.NbPoints(); ++i) { Standard_Real aParam = aPointSampler.Parameter(i); gp_Pnt aP = aCurveAdaptor->Value(aParam); gp_Vec aT; gp_Vec aN; gp_Vec aB; aFrenet->D0(aParam, aT, aN, aB); // vtrihedron in opencascade draw 6.9.1 /*aTclFile << \"vtrihedron vt\" << i << \" \" << aP.X() << \" \" << aP.Y() << \" \" << aP.Z() << \" \" << \" \" << aB.X() << \" \" << aB.Y() << \" \" << aB.Z() << \" \" << \" \" << aT.X() << \" \" << aT.Y() << \" \" << aT.Z() << std::endl;*/ // vtrihedron in opencascade draw 7.1.0 has bug. /*aTclFile << \"vtrihedron vt\" << i << \" -origin \" << aP.X() << \" \" << aP.Y() << \" \" << aP.Z() << \" \" << \" -zaxis \" << aB.X() << \" \" << aB.Y() << \" \" << aB.Z() << \" \" << \" -xaxis \" << aT.X() << \" \" << aT.Y() << \" \" << aT.Z() << std::endl;*/ // vtrihedron in opencascade draw 7.2.0 aTclFile << \"vtrihedron vt\" << i << \" -origin \" << aP.X() << \" \" << aP.Y() << \" \" << aP.Z() << \" \" << \" -zaxis \" << aB.X() << \" \" << aB.Y() << \" \" << aB.Z() << \" \" << \" -xaxis \" << aT.X() << \" \" << aT.Y() << \" \" << aT.Z() << std::endl; aTclFile << \"vtrihedron vt\" << i << \" -labels xaxis T 1\" << std::endl; aTclFile << \"vtrihedron vt\" << i << \" -labels yaxis N 1\" << std::endl; aTclFile << \"vtrihedron vt\" << i << \" -labels zaxis B 1\" << std::endl; aTclFile << \"vsize vt\" << i << \" 2\" << std::endl; } } int main(int argc, char* argv[]) { test(); return 0; }
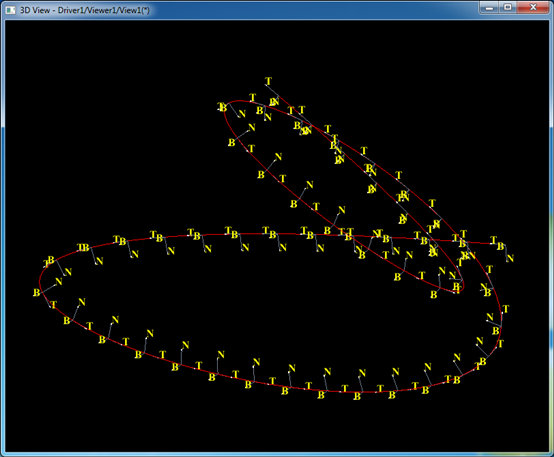
程序通过拟合几个随机产生的点生成B样条曲线,再将曲线按弧长等距采样,将得到的参数计算出曲线上的点,及Frenet标架。再生成Draw脚本文件,最后将生成的Draw脚本文件trihedron.tcl加载到Draw Test Harness中显示结果如下图所示:
Figure 3. Frenet Frame
由上图可知,局部坐标系的T方向为曲线的切线方向。主法向N总是指向曲线凹侧。
4. Conclusion
曲线的活动标架是《微分几何》中一个很基础的概念。有了曲线的活动标架,扫掠造型Sweep算法的实现有了一些思路。当给定一个轮廓线后,将轮廓线沿着路径曲线扫掠可以理解为将轮廓线变换到曲线的活动标架中。
本文主要演示了Frenet活动标架的例子,读者可以将GeomFill_TrihedronLaw其他的子类表示的其他类型活动标架自己实现,加深理解。
5. References
1. 赵罡, 穆国旺, 王拉柱. 非均匀有理B样条. 清华大学出版社. 2010
2. 陈维桓. 微分几何. 北京大学出版社. 2006
3. 朱心雄. 自由曲线曲面造型技术. 科学出版社. 2000


![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)











暂无评论内容