OpenCASCADE点向圆柱面投影

eryar@163.com

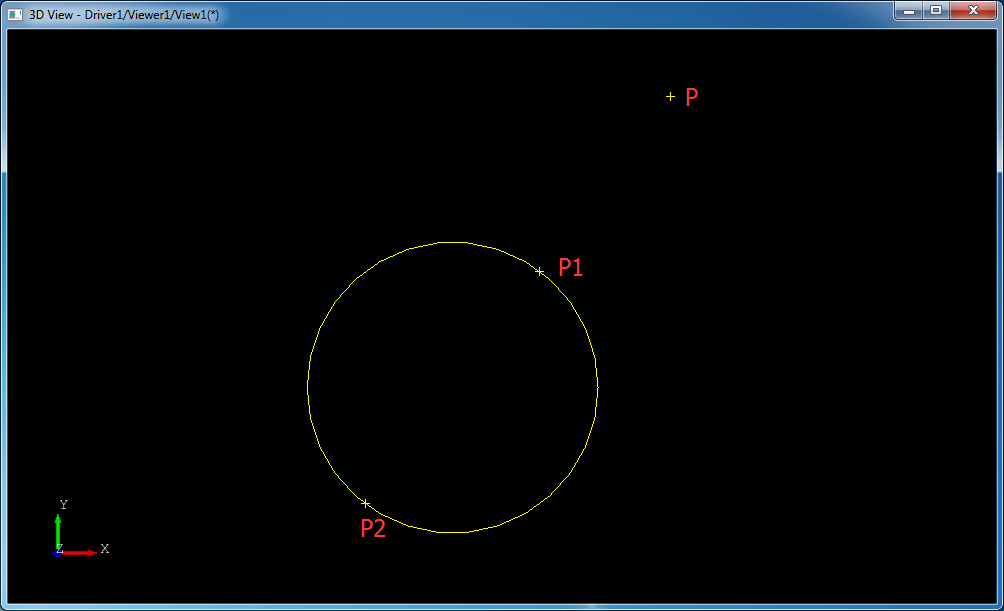
OpenCASCADE的类Extrema_ExtPElS提供了点到基本曲面的投影计算功能，距离可能是最大值或是最小值。如下图所示的点到圆柱的投影会有两个投影点P1和P2，则点到圆柱的距离的最小值是P到P1的距离，最大值是P到P2的距离。本文主要是对此类中点到圆柱的投影算法进行分析。

类Extrema_ExtPElS类中计算点到圆柱的投影源码列出如下：

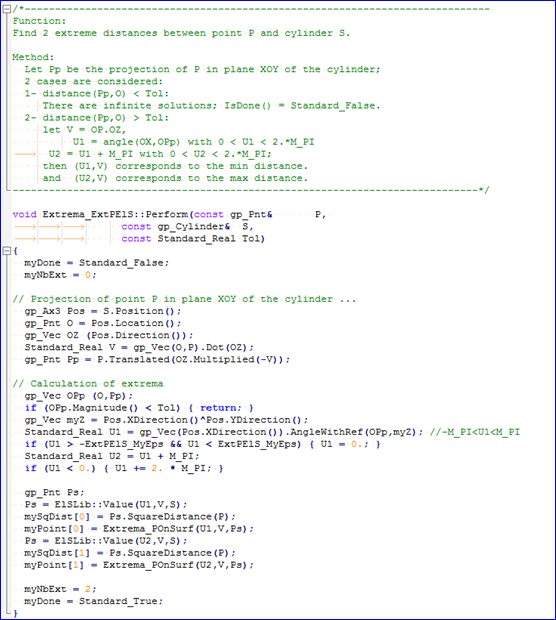
结合源码的注释可以看出点P到圆柱S的投影主要按有如下步骤：

l 计算点P到以圆柱S轴线为法线的平面的投影点Pp；

l 若点P在轴线上，则计算失败返回；

l 计算点Pp在圆柱U方向的参数U1（角度）；

l 将参数U1（角度）加180度得到参数U2；

l 计算参数（U1，V），（U2，V）对应在圆柱面上的点；

上述实现主要也是使用向量的运算，所以程序简单且性能高。其中保存的距离是距离的平方值，这种方式主要考虑的是自带的开方函数性能，除非后面要用到距离才会自己去开方，这样也是提供性能的一种处理方式。

OpenCASCADE的向量类gp_Vec提供了一个函数AngleWithRef()，查看源码可知这个函数主要是计算两个向量之间的夹角，其中参数向量Ref是用来处理角度的正负。当两个向量叉乘的向量与参考向量Ref反向时，也会将得到的角度值取负。

下面通过一个简单的小程序来将计算结果在Draw Test Harness中可视化，这样可以直观地验证一下：

将生成的脚本文件加载到DRAW中得到如下图所示的结果：

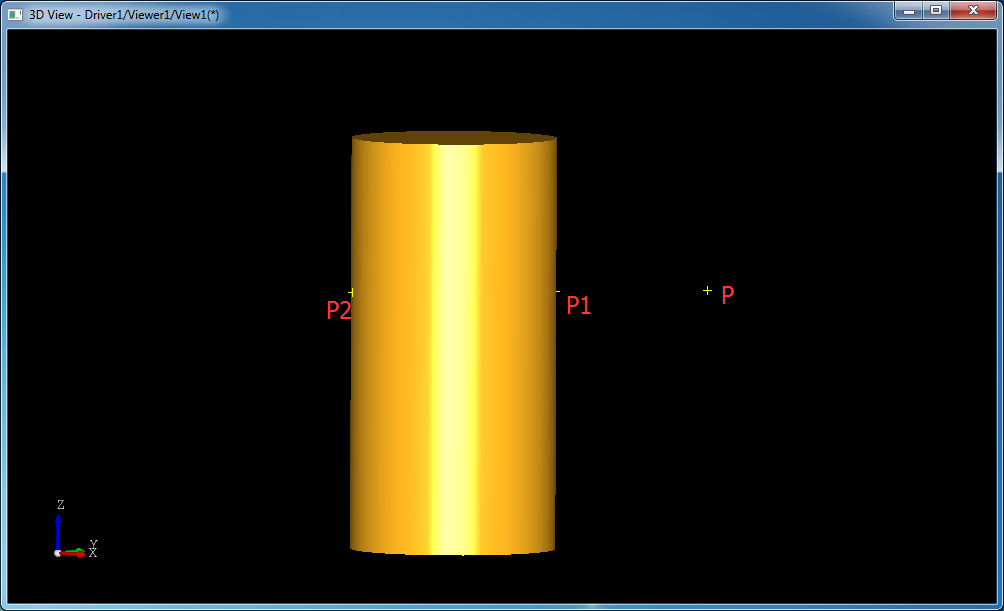
从上图可以看出，投影得到的两个点P1，P2的高度值与点P是相同的。