HRTF Adaptation Tool in Matlab
This tool consists of a set of matlab functions and GUIs to provide an customization process of HRTFs using three open access HRTF databases.
Individual head-related transfer functions (HRTFs) can be used to generate
virtual sound sources over headphones. According to the model of
HRTF individualization using Principal Components (PCs), a Principal
Component Weight (PCW) set is sought that when multiplied with a PC
basis results in an HRTF set that yields good localization for a number of
given directions of sound incidence. Although this is a promising model,
the extent to which listeners can perform the individualization by hearing
is debatable. The process requires adjustment for each location and PC
of interest.
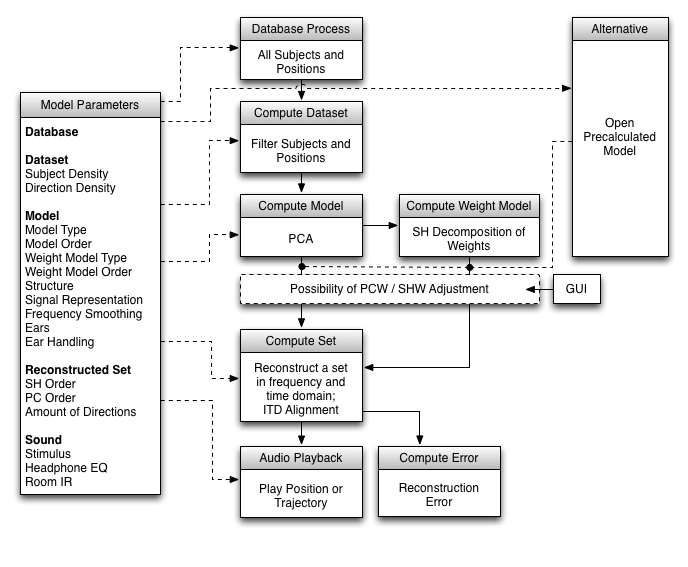
![图片[1]-HRTF-Individualization-卡核](wp-content/uploads/2023/04/hrtf_ adaptation_process.png) In this work, the feasibility of a local and global method is
In this work, the feasibility of a local and global method is
numerically evaluated by estimating the accuracy with which a given basis
component can model HRTFs regarding different kinds of input data. The
number of required adjustments for a given direction set is then reduced
by decomposing the PCW of individual users upon a Spherical Harmonics
Basis. Optimal spherical model parameters are sought, depending on the
order and reconstruction accuracy. In a listening test, subjects were asked
to identify changes in localization when weights of individual directions
are automatically modified. This allows a deeper inside into the usability
of each technique.
Requirements
-
Matlab
-
At least one of these open access HRTF databases:
- ARI (Acoustics Research Institute) with 85 subjects and 1550 source positions
- CIPIC (University of California at Davis) with 45 subjects and 1250 source positions
- IRCAM (Institut de Recherche et Coordination Acoustique/Musique) with 50 subjects and 187 source positions
Please download these databases and copy the content into the directory db/.
Getting Started
- Clone or download this repository:
git clone https://github.com/jhoelzl/HRTF-Individualization.git - Add at least one of the HRTF databases listed above and extract the contents into
db/database-name/. Alternatively you can use a custom HRTF database and add the import function inmodel/matlabcode/functions/core/database_import.m. - Adjust your active HRTF databases in
model/matlabcode/config.xml - In Matlab add
model/matlabcodeto the search path (useaddpathor go through menu settings) - Go to Matlab code directory:
cd model/matlabcode - Run
gui_modelin Matlab. A graphical user interface like in the screenshot below should appear.
HRTF Model
Graphical User Interface
Mathematical Background
Principal Component Analaysis (PCA)
Principal Component Analysis is a robust statistical method for data representation. The technique projects an original dataset on an orthogonal subspace that is estimated by taking the covariance of the data into account. The technique can be used to unveil relationships between the independent variables in a dataset and in this way reduce a high-dimensional dataset into a more meaningful, low-dimensional space. It has been widely used in computer vision and pattern recognition to find relevant structure in data and neglect redundant information. Usually the input data is pre-processed and aligned prior PCA to increase the performance. The resulting model parameters can be calculated directly from the input data through Singular Value Decomposition (SVD). Through a linear combination of the new basis and their corresponding principal weights, the original dataset can be reconstructed with a controllable accuracy, because the orthogonal principal components are sorted according to their variance describing the original data.
Spherical Harmonic Decomposition (SH)
Spherical Harmonic Decomposition, primary intended for the modeling and approximation of continuous functions on the sphere, has also been applied to model HRTFs. As HRTF measurements occur for positions distributed on a sphere, or spherical sections, such an approach is inherently appropriate. The dataset is projected onto spherical basis functions of a desired order, whose weighted combination can be used for modeling or approximation purposes. In contrast to PCA, where the basis functions are computed from the dataset, the spherical harmonic functions are fixed and defined hierarchically.
Conclusion
Diploma Thesis
- Title: A Global Model for HRTF Individualization by Adjustment of Principal Component Weights
- Author: Josef Hölzl
- Date: March 2014
- Host Institution: Institute of Electronic Music and Acoustics, University of Music and Performing Arts Graz, Graz University of Technology
Project Thesis
- Title: An initial Investigation into HRTF Adaptation using PCA
- Author: Josef Hölzl
- Date: July 2012
- Institute of Electronic Music and Acoustics, Graz, Austria