卡核推荐：深入剖析三维几何内核(4)–曲面的艺术

本文原文：多物理场仿真技术

几何曲面地位

在B-Rep拓扑结构中，我们知道实体Solid是由Face构成的，Face和Surface几何面关联（如图），因此在实体内部不存在数据，这个与体渲染形成了鲜明对比，体渲染在实体内部存在数据，也就是说用一个平面切开体渲染实体后，能够得到截面上任意一点的数据。

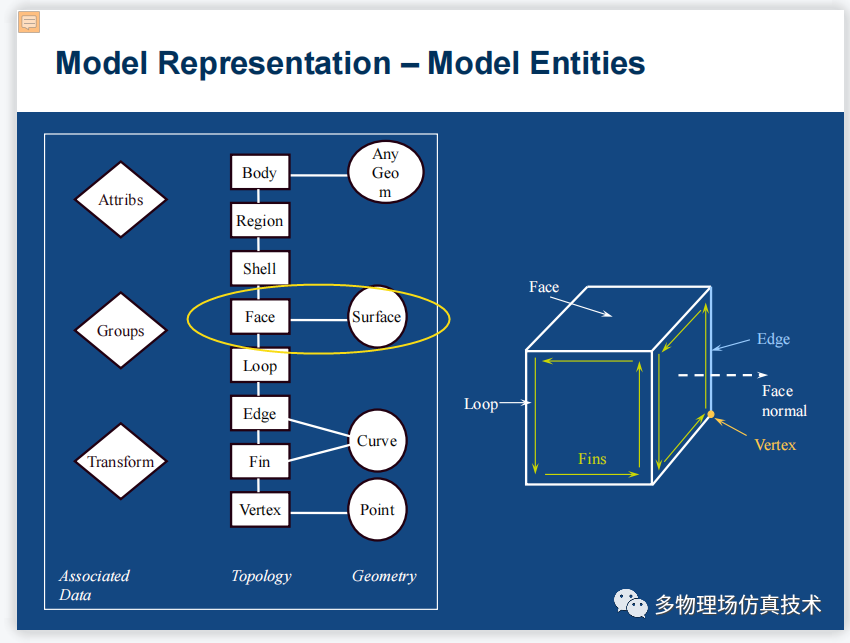
Parasolid几何面与拓扑面对应关系

所以从数据结构上来看，几何面的创建和处理是三维内核几何操作最核心的功能，几何面处理好了，其它几何操作都不是问题。从以下Parasolid的结构图中我们也可以看到曲面占据了几何主要地位。

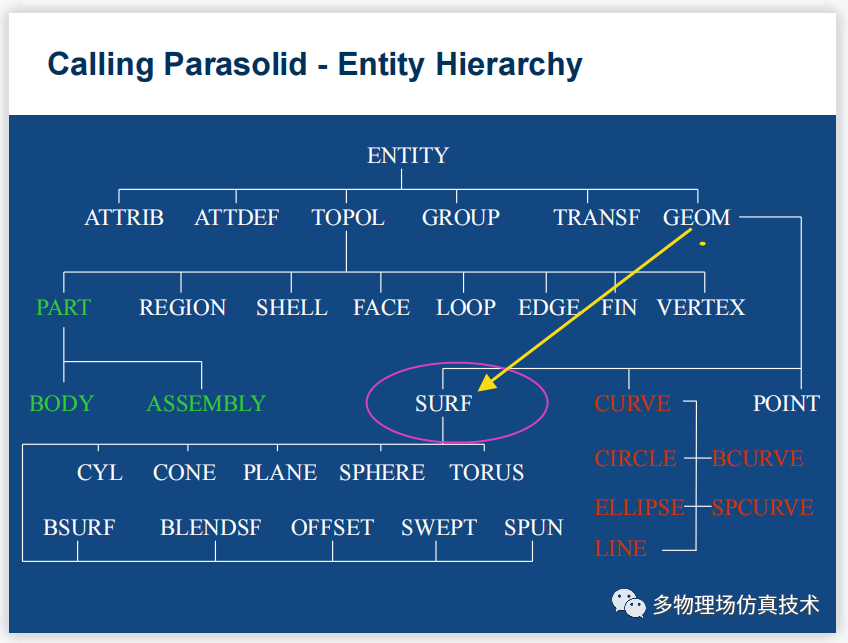
Parasolid实体结构图

曲面 Curved Surface，通常包含了我们所说的各种几何面(Surface)，常见的平面（Planar Surface）是曲面的一种特殊形式。

在实际生活中我们绝少见到方方正正的设计，大部分都是需要用曲面处理。

规整的汽车

各种奇特外观建筑是曲面设计的用武之地

发动机，螺旋桨对曲面设计和制造都有非常高的要求

曲面类型

通常我们将曲面分为两种：解析曲面和样条曲面，又叫插值曲面。

很好理解，解析曲面有函数表达式f(x,y,z)，即给出任意坐标值，可以准确的计算出该坐标的数据，有点类似偏微分方程的解析解，解析曲面通常可以高阶连续，在研究特定图形时很有用。解析曲面虽然是解析解，但很多时候能够构造出非常奇异的形状。如下图：

以上图片来自网络

正如偏微分方程很难找到解析解一样，工程中设计很难找到预先定义好的用函数定义的曲面，设计中更多使用的离散点生成样条曲线，再利用样条曲线构成样条曲面。

曲线类型

回顾一下样条曲线的相关知识。

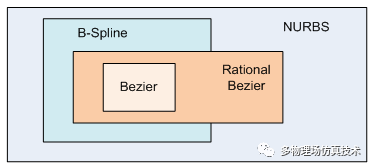
1.贝塞尔曲线

2.有理贝塞尔曲线

3.B样条曲线

4.NURBS曲线（非有理样条曲线）

5.T样条曲线

以上图片来源于网络

样条曲线1,2,3是NURBS曲线的特殊形式。设计曲线时，通常会给出一系列的离散点，再用曲线将该离散点拟合，形成不同的拟合表达式。拟合方式的不同构成不同的曲线。曲线通常使用控制点，控制点权重，基函数阶数，分段拟合表达式等来控制曲线生成。

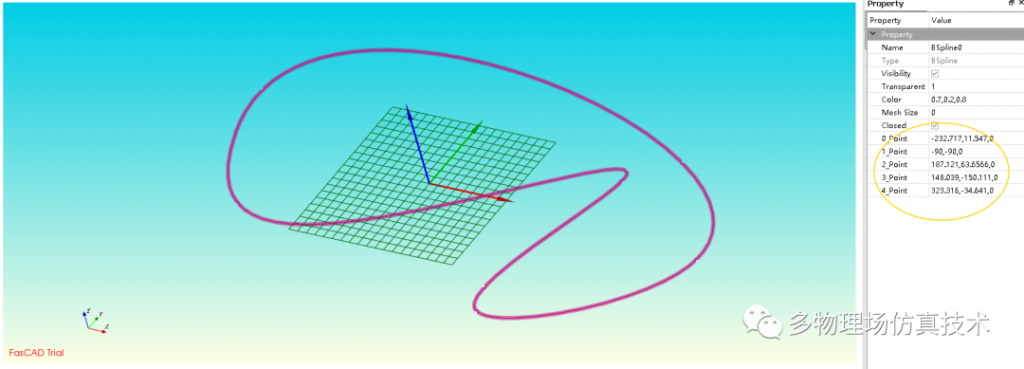
下图显示了FasCAD中利用多个控制点生成封闭B样条曲线

T样条曲线(T-Spline)是在2003年出现的一种新形式的样条曲线，最早放在Rhino作为插件使用。相比NURBS，生成相同的曲线，T样条曲线只需更少的控制点，和NURBS曲线也可以互转。

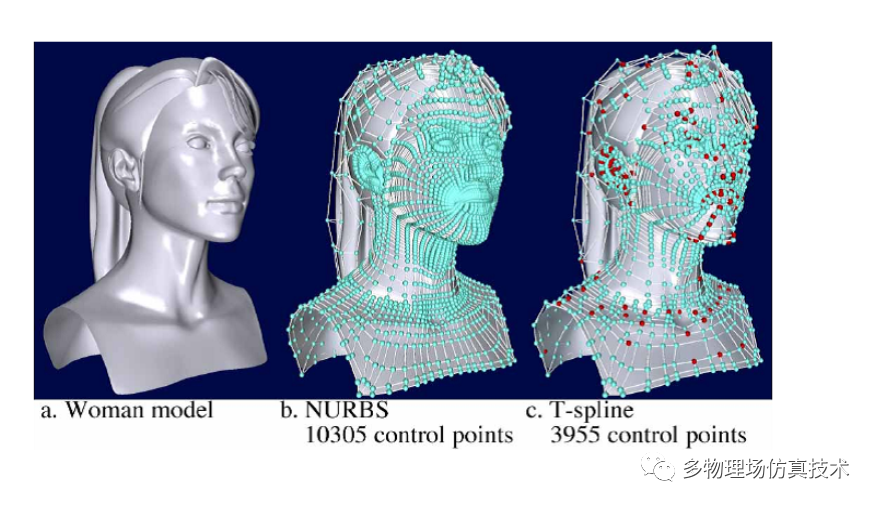
T样条控制点只需NURBS的大约1/3

关于样条曲线的理论计算和设计实现可以参考附录1.

曲面生成

曲面参数

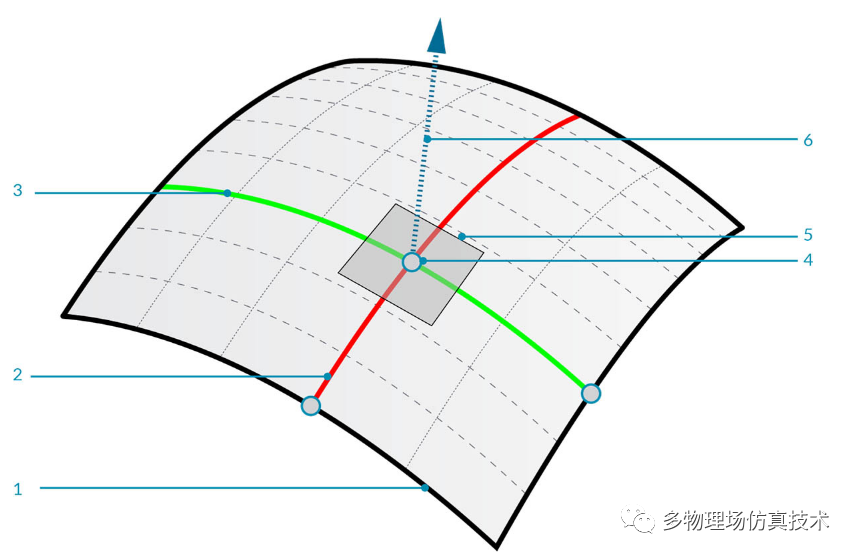
图片来源于Dynamo Primer

1. 曲面
2. U 向等参曲线
3. V 向等参曲线
4. UV 坐标
5. 垂直平面
6. 法线向量

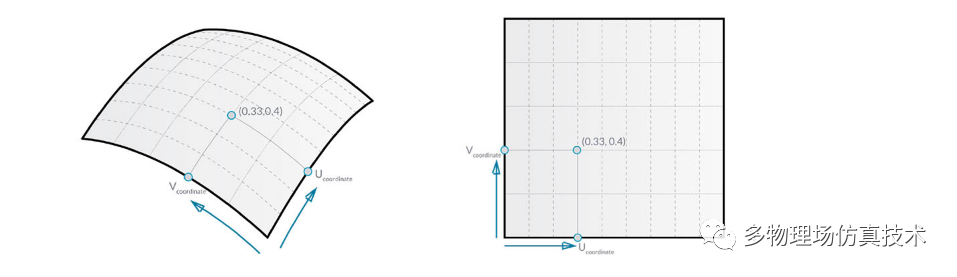
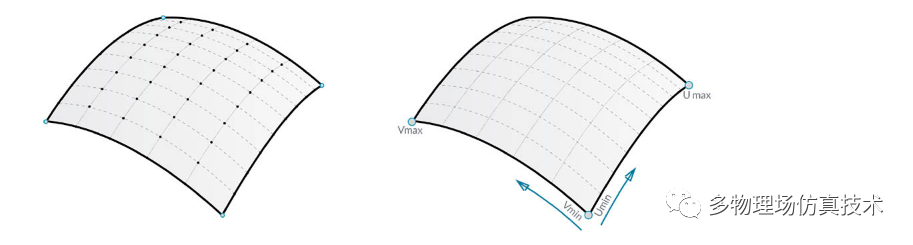
任意曲面可以建立到规则平面的映射

NURBS 曲面是最通用的一种曲面形式

NURBS 曲面与 NURBS 曲线非常相似。可以将 NURBS 曲面视为位于两个方向上的 NURBS 曲线的栅格。NURBS 曲面的形状由多个控制点以及该曲面在 U 和 V 方向的阶数定义。相同的算法用于通过控制点、权重和阶数来计算形状、法线、切线、曲率和其他属性。

Parasolid中的曲线和曲面类型

了解了曲面的基本参数，下面看看在设计中如何生成曲面

1.扫掠

扫掠是规则曲面的常用方法，包括路径扫掠，自定义规则扫掠。绕轴360度旋转是一种特殊的扫掠。

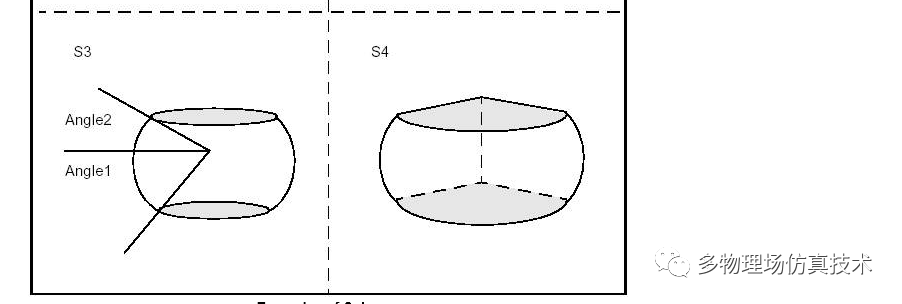
圆弧扫掠生成鼓

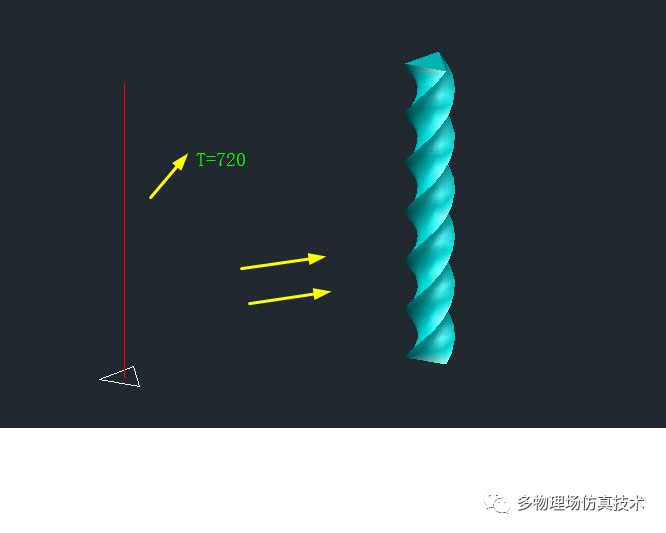
封闭多义线螺旋扫掠

2.曲线拟合

多条曲线拟合成新面

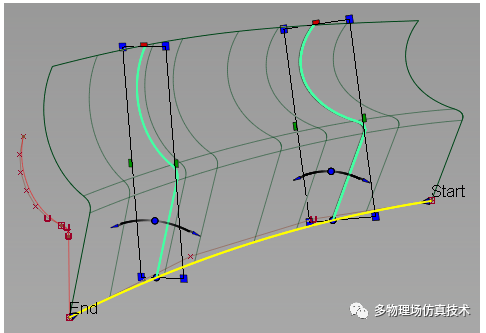
应用场景之一：

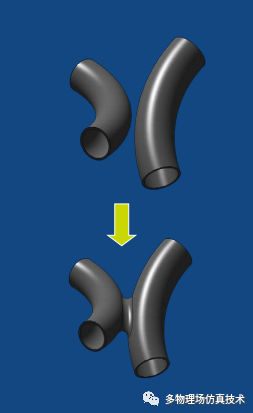
Faces Blend操作

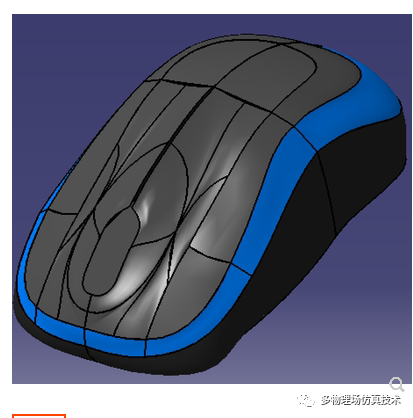
一个简单鼠标全部由自由曲面构成

3. 模板

模板是事先定义好的曲线方程，或者控制点预先定义好的Pattern。最常见的模板就是圆角倒角。CAD软件中，用户并不需要实际设计圆倒角几何，修改简单的参数即可生成相应的倒角模型。

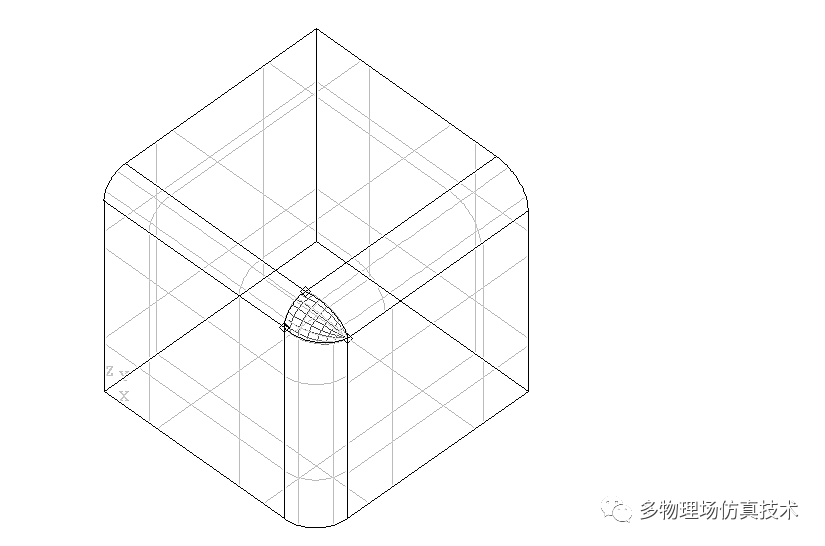
倒角并不是简单的球面

曲面连续性

连续性是曲面的一个重要特征，反应了曲面的光滑程度和质量。

 Geometric continuity，通常记作G(N)，N表示曲线或曲面可连续可求导的阶数。G(N)的连续性是独立于表示（参数化）的。

G0两个对象相连或两个对象的位置是连续的。G0连续（也称为点连续）在每个表面上产生一次反射，这种连续仅仅保证曲面间没有缝隙而是完全接触。

G1两个对象光顺连续，一阶微分连续，或者是相切连续的。G1连续（也称为切线连续）将产生一次完整的表面反射，反射线连续但是扭曲，这种连续仅是方向的连续而没有半径连续。我们通常的倒圆角就是这种情况。

G2两个对象光顺连续，二阶微分连续，或者两个对象的曲率是连续的。G2连续（也称为曲率连续）将产生横过所以边界的完整的和光滑的反射纹。曲率连续意味着在任何曲面上的任一“点”中沿着边界有相同的曲率半径。外观质量要求高的产品需要曲率做到G2连续，其实曲面做到这一点难度很大。

G3两边对象光顺连续，三阶微分连续等

曲面的布尔运算

曲面布尔运算是比较容易出问题的地方，主要在于面被裁剪后，一方面需要重新计算端点，曲边需要重新插值计算，造成容差问题；另一方面如果曲面在相交面上，新生成的截面在仿真划分网格时会导致网格不匹配。在曲面布尔运算时，尽可能用曲面参数计算，对于存在非二维流形和截面的情况，需要保存双面的映射关系，而不能仅仅让B-Rep结构来处理。

曲面的显示

曲面曲线的显示类似于圆弧和圆面的显示，圆弧需要将曲线离散成小段直线，圆面需要离散成三角形，圆周为连接的小线段。需要注意的是边界离散长度确定，通常利用弦高比，即计算曲线上点的切向和角度。参考OCC里网格生成方法：

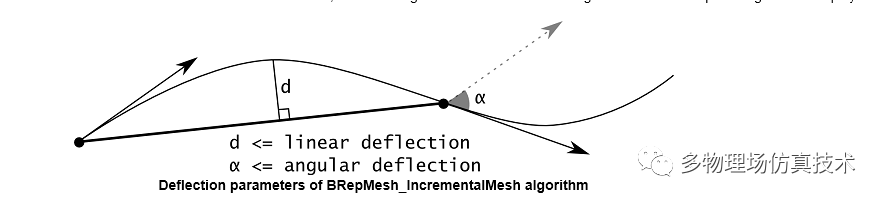
对于设计类CAD软件，曲线的显示最好能采用矢量方法，以避免视图显示和实际几何产生误差。

软件参考

商业软件方面，一般三维CAD软件都有曲面建模功能，但从工业软件和总体功能和效率上看，犀牛Rhino和CATIA在曲面建模上更有优势。

总结

曲面处理的理论基础和计算是几何中最复杂的，也是衡量一个三维几何内核质量的重要指标。本文在之前文章的基础上进一步介绍了几何内核曲面的相关基础知识，其涉及到的理论公式都没有列出，有兴趣的读者可参考附录以及相关书籍。

附录

1. 计算机辅助几何设计与非均匀有理B样条，作者：施法中

2. 曲面几何学，作者：John·Stillwell

3. 曲线与曲面的微分几何， 作者 ：Manfredo P.Do Carmo