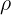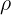和  这两种表达式经常出现在流体力学公式中，尽管两者形式很相近，但是表达的意义却大相径庭。这次我们通过介绍梯度和散度，来掌握一些公式化简的技巧。

1. 梯度算子

什么叫梯度算子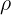？    这个表达式看似是一个整体，实际上却是由两个物理符号组成。 其中  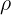 是一个物理量，可以是密度、压力、温度等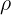，  就是梯度算子。

梯度算子是高等数学的一个概念，表示空间各方向上的全微分，表达式为：

从表达式我们能够看出，实际上梯度算子是一个向量，只不过这个向量的各个分量是微分形式。如果有其他的物理量与其结合，就能够组成一些表达式。

2. 梯度

了解了什么是梯度算子之后，我们能够很容易的得到梯度公式。梯度本质上就是梯度算子与一个物理量相乘，如 

 由于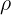为密度，是一个标量物理量，因此直接将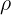乘进括号即可，得：

公式3即为密度的梯度 。

注：

1） 梯度是一个向量，一个标量函数的梯度记为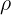： 或grad 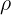 。在三维直角坐标中表示为  ；如函数  的梯度为  。

2） 梯度的方向表示标量变化最快的方向，梯度的模表示标量变化最快方向的变化量及最大变化量。

3） 柱坐标下的梯度算符

此处的加法并非数学运算的加法，而是向量的表达方法。其中分别是柱坐标下三个方向（径向、切向和轴向）的单位向量

3. 散度

散度（divergence）可用于表征空间各点矢量场发散的强弱程度，物理上，散度的意义是场的有源性

对于一个矢量场F而言，散度有两种不同的定义方式。第一种定义方式和坐标系无关：

第二种定义方式则是在直角坐标系下进行的：

从第二种定义方式来看，散度实际上是梯度算子与一个矢量物理量点乘，这个矢量物理量在流体力学中一般为速度V。因此将散度展开书写为公式（4），两个向量的点乘等于各个分量相乘再相加，也就是上式。

注：

1）梯度为向量，而散度为标量。

2）梯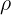度  和散度 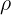  符号类似，但两者意义相差甚大。梯度的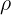为标量，其意义是对三个方向分别求偏导。而散度的V为矢量，表示的是梯度算子与矢量V的点乘，求和之后为标量。

4.举例

        对于流体力学连续性方程公式（5）进行简化表达。

 对于这个方程我们可以看到，方程左边第二项到第四项可以写成  ，方程左边后三项可以简写成。因此式5可以简写为:

 而6式的第一项和第二项实际上为密度的随体导数（关于随体导数，也是流体力学中常出现的符号），可以写作,因此6式可写为：

当流体为不可压缩流体时，密度为常数，此时，公式7为：

 公式8即为我们经常遇到的不可压缩流体的连续性方程。

5.总结

       梯度和散度只是流体力学中两个比较基本的概念，还有一些其他的知识点需要我们掌握，比如拉普拉斯算子、雷诺输运方程、高斯定理等，当掌握这些知识之后，流体力学的三大守恒公式就可以自行推导了。

以上案例的cas和dat文件均可以免费获取，需要的朋友，只需要点赞关注收藏一键三连后私信我即可哦