一、概述

确定性推理是人工智能经典三大基本技术（知识表示、推理、搜索策略）之一。
推理是人类求解问题的主要思维方法，智能系统的推理过程实际上是一个思维过程。

为方便记忆和回顾，根据个人学习，总结人工智能基础知识和思维导图形成系列。

二、重点内容

推理的概念
推理的分类，常用推理方式的特点
推理的方向
自然演绎推理基本规则
归纳演绎推理的基本步骤
归纳演绎推理中谓词公式的化简、谓词逻辑的归结，以及归结演绎推理的归结策略

三、思维导图

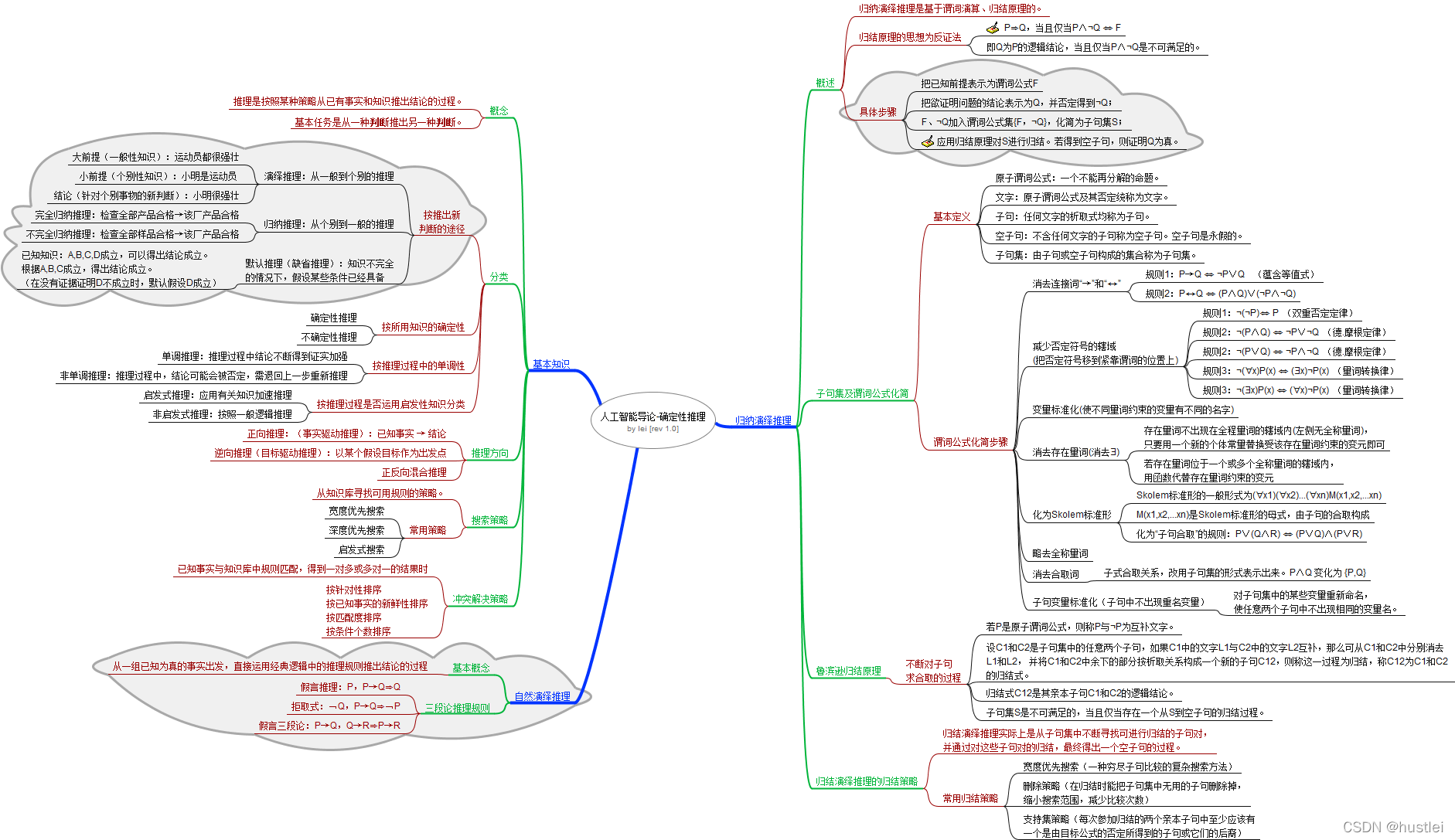
人工智能导论(3)——确定性推理

四、重点知识笔记

1. 推理基本知识

1.1 推理的基本概念

推理是按照某种策略从已有事实和知识推出结论的过程。

医疗诊断专家系统为病人诊治疾病就是一次推理过程

知识库存储专家的经验及医学常识

数据库存放病人的症状、化验结果等初始事实

推理：1）从数据库病人初始事实出发，2）利用知识库中的知识及一定的控制策略，3）对病情做出诊断，并开出医疗处方。

推理的基本任务是从一种判断推出另一种判断。

1.2 推理的分类

人类的思维方式有多种，相应的有多种推理方式。推理从不同的角度有不同的分类方式

1.2.1 按推出新判断的途径分类

1） 演绎推理：从一般到个别的推理。

演绎推理中最常用的形式是三段论法。

三段论由三个判断组成：

大前提（一般性知识）：运动员都很强壮
小前提（个别性知识）：小明是运动员
结论（针对个别事物的新判断）：小明很强壮

2） 归纳推理：从个别到一般的推理

从足够多的个别实例归纳出一般性结论。

完全归纳推理：检查全部产品合格→该厂产品合格
不完全归纳推理：检查全部样品合格→该厂产品合格

归纳推理是人类思维活动中最基本、最常用的一种推理形式。

3） 默认推理（缺省推理）：知识不完全的情况下，假设某些条件已经具备

已知：A,B,C,D成立，可以得出结论成立。

默认推理：A,B,C成立，得出结论。（在没有证据证明D不成立时，默认假设D成立）

1.2.2 按所用知识确定性分类

确定性推理：所有知识都是精确的，按因果关系进行逻辑推理。
不确定性推理：根据不精确和含糊的主观判断推理，结论正确性不确定。
- 似然推理（概率论）
- 近似推理或模糊推理（模糊逻辑）

1.2.3 按推理过程中的单调性

单调推理（基于经典逻辑的演绎推理）：随着推理向前推进及新知识的加入，推论不断加强，推出的结论越来越接近最终目标。
非单调推理（默认推理是非单调推理）：由于新知识的加入，不仅没有加强已推出的结论，反而要否定它，使推理退回到前面的某一步，重新开始。

人类的推理过程通常都是非单调的。

非单调推理示例：

知识：x=鸟 → x会飞

新知识：x=企鹅 → x不会飞

推论：x会飞？不会飞？

1.2.4 按推理过程是否运用启发性知识分类

启发式推理：应用与问题有关且能加快推理过程、提高搜索效率的知识（策略、技巧、经验等）进行推理。
非启发式推理：按照一般的控制逻辑进行推理，容易出现“组合爆炸”问题，效率低。

1.3 推理的控制策略

1.3.1 推理方向

正向推理（事实驱动推理）：已知事实 → 结论
1. 从初始已知事实出发
2. 在知识库中找出可适用的知识（搜索策略）
3. 冲突解决，选出一条知识推理（冲突消解策略）
4. 重复2-3步骤
逆向推理（目标驱动推理）：以某个假设目标作为出发点
1. 选定一个假设目标
2. 寻找假设目标的证据（如何判断是否是证据，多条）
  - 所有证据都找到，假设成立
  - 找不到所需的证据，假设不成立，另作新假设
正反向混合推理
1. 根据初始事实进行正向推理，帮助提出假设
2. 反向推理进一步寻找支持假设的证据
3. 反复1-2步骤

正向推理易实现、目的性不强，效率低。

逆向推理目的性强，起始假设目标的选择具有盲目性。

正反向混合推理集中了正向推理和反向推理的优点，但其控制策略相对复杂。

1.3.2 搜索策略

从知识库寻找可用规则的策略。

常用的有：

状态空间搜索
- 宽度优先搜索
- 深度优先搜索
- 有界深度优先搜索
启发式搜索

1.3.3 冲突解决策略

已知事实与知识库中规则匹配的三种情况：

恰好匹配成功（一对一）
不能匹配成功
多种匹配成功（一对多，多对一）

多种匹配成功需要进行冲突消解。

常用冲突解决策略：

按针对性排序
按已知事实的新鲜性排序
按匹配度排序
按条件个数排序

2. 自然演绎推理

2.1 基本概念

从一组已知为真的事实出发，直接运用经典逻辑中的推理规则推出结论的过程

2.2 推理规则

最基本规则是三段论推理：

假言推理：P，P→Q⇒Q
拒取式：﹁Q，P→Q⇒﹁P
假言三段论：P→Q，Q→R⇒P→R

优缺点同谓词逻辑

3. 归纳演绎推理

归纳演绎推理是基于谓词演算、归结原理的。

归结原理的思想为反证法：
P⇒Q，当且仅当P∧¬Q⇔F。即Q为P的逻辑结论，当且仅当P∧¬Q是不可满足的。

具体步骤为：

把已知前提表示为谓词公式F。
把欲证明问题的结论表示为Q，并否定得到¬Q；
F、¬Q加入谓词公式集{F，¬Q}，化简为子句集S；
应用归结原理对S进行归结。若得到空子句，则证明Q为真。

子句集、化简方法及归结原理知识如下：

3.1 子句集及谓词公式化简

3.1.1 基本定义

原子谓词公式：一个不能再分解的命题。
文字：原子谓词公式及其否定统称为文字。（例如，P(x)、Q(x)、P(x) ¬ 、¬Q(x)等都是文字。）
子句：任何文字的析取式均称为子句。（例如，P(x) ∨ Q(x)、P(x, f (x)) ∨ Q(x, g(x))都是子句。）
空子句：不含任何文字的子句称为空子句。空子句是永假的。（空子句一般被记为NIL。）
子句集：由子句或空子句构成的集合称为子句集。

如果P，一定Q，记作P⇒Q，即P为Q的前提。
对于定义域D，P与Q的值都相同，则称P和Q时等值的，记作P⇔Q。

3.1.2 谓词公式的化简

步骤如下：

消去连接词“→”和“↔”
- 规则1：P→Q ⇔ ¬P∨Q
- 规则2：P↔Q ⇔ (P∧Q)∨(¬P∧¬Q)
减少否定符号的辖域(把否定符号移到紧靠谓词的位置上)
- 规则1：¬(¬P)⇔ P （双重否定定律）
- 规则2：¬(P∧Q) ⇔ ¬P∨¬Q （德.摩根定律）
- 规则2：¬(P∨Q) ⇔ ¬P∧¬Q （德.摩根定律）
- 规则3：¬(∀x)P(x) ⇔ (∃x)¬P(x) （量词转换律）
- 规则3：¬(∃x)P(x) ⇔ (∀x)¬P(x) （量词转换律）
变量标准化(使不同量词约束的变量有不同的名字)
- 把谓词公式中受该量词约束的变元全部用另外一个没有出现过的任意变元代替。
消去存在量词(消去∃)
- 存在量词不出现在全程量词的辖域内(左侧无全称量词)。
  - 只要用一个新的个体常量替换受该存在量词约束的变元即可
- 若存在量词位于一个或多个全称量词的辖域内
  - 用函数代替存在量词约束的变元，函数被称为Skolem函数
  - (∀x)(∃y)P(x,y)中，存在y可能依赖于x值，依赖关系由函数f(x)定义，用f(x)替换y，写成(∀x)P(x,f(x))
化为前束范式(所有量词都移到公式的左边)
- 因为第3步已经进行了变量标准化，每个量词都有自己的变元，所以移动不改变语义
化为Skolem标准形
- Skolem标准形的一般形式为(∀x1)(∀x2)…(∀xn)M(x1,x2,…xn)
- M(x1,x2,…xn)是Skolem标准形的母式，由子句的合取构成
- 化为“子句合取”的规则：P∨(Q∧R) ⇔ (P∨Q)∧(P∨R)
略去全称量词
- 母式中的全部变元均受全称量词的约束，全称量词的次序已无关紧要，因此，可以省掉全称量词
消去合取词
- 子式合取关系，改用子句集的形式表示出来。P∧Q 变化为 {P,Q}
子句变量标准化（子句中不出现重名变量）
- 对子句集中的某些变量重新命名，使任意两个子句中不出现相同的变量名。

3.2 鲁滨逊归结原理

归结就是不断对子句求合取的过程。

若P是原子谓词公式，则称P与¬P为互补文字。
设C1和C2是子句集中的任意两个子句，如果C1中的文字L1与C2中的文字L2互补，那么可从C1和C2中分别消去L1和L2，
并将C1和C2中余下的部分按析取关系构成一个新的子句C12，则称这一过程为归结，称C12为C1和C2的归结式。
归结式C12是其亲本子句C1和C2的逻辑结论。
子句集S是不可满足的，当且仅当存在一个从S到空子句的归结过程。