人工智能导论(4)——不确定性推理(Uncertainty Reasoning)

07896367

文章目录

一、 概述

人工智能经典三大基本技术为：知识表示、推理、搜索策略。推理是人类求解
问题的主要思维方法。

无论是人类智能还是人工智能，都离不开不确定性的处理。
可以说，智能主要反映在求解不确定性问题的能力上。
因此，不确定性推理模型是人工智能和专家系统的一个核心研究课题。

为方便记忆和回顾，根据个人学习，总结人工智能基础知识和思维导图形成系列。

二、 重点内容

  • 不确定性推理的概念及分类
  • 不确定性推理中的基本问题
  • 概率方法及贝叶斯公式
  • 可信度方法
  • 模糊推理

三、 思维导图

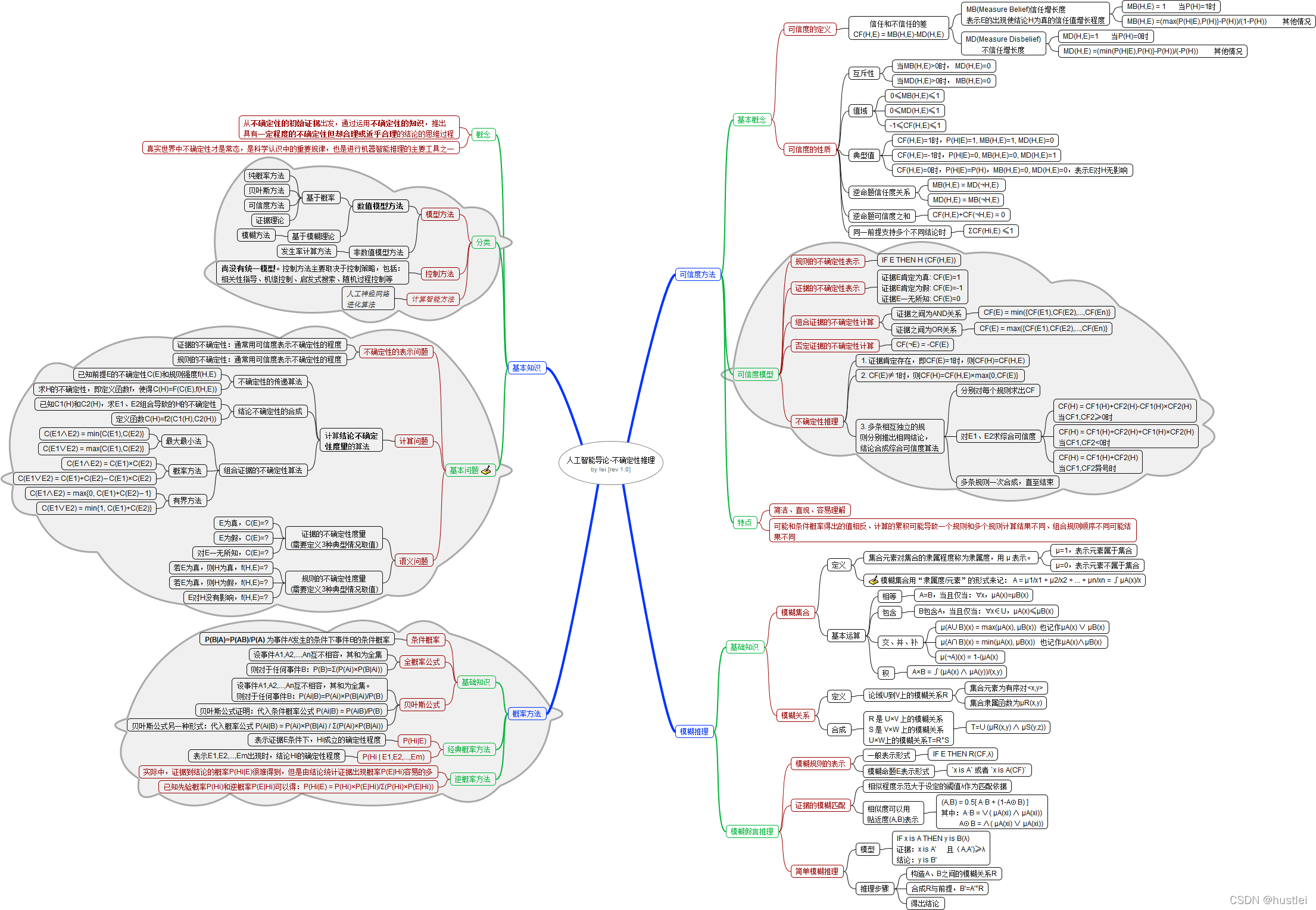
人工智能导论(4)——不确定性推理

四、 重点知识笔记

1. 不确定性推理概述

1.1 概念

不确定性推理是指从不确定性的初始证据出发，通过运用不确定性的知识，
推出具有一定程度的不确定性但却合理或近乎合理的结论的思维过程。

不精确性是科学认识中的重要规律，也是进行机器智能推理的主要工具之一。

1.2 分类

不确定性推理方法主要分为控制方法和模型方法两类。

  • 模型方法
    • 数值模型方法
      • 基于概率
        • 概率方法（纯概率法应用受限）
        • 贝叶斯方法
        • 可信度方法
        • 证据理论
      • 基于模糊理论
        • 模糊方法
    • 非数值模型方法
      • 发生率计算方法
  • 控制方法
    • 尚没有统一模型。相关性指导、机缘控制、启发式搜索、随机过程控制等

控制方法

控制方法没有处理不确定性的统一模型，其效果极大地依赖于控制策略。

不确定性推理的控制方法主要取决于控制策略，包括相关性指导、机缘控制、启发式
搜索、随机过程控制等。

模型方法

模型方法具体可分为数值模型方法和非数值模型方法两类。按其依据的理论不同，
数值模型方法主要有基于概率的方法和基于模糊理论的推理方法。

纯概率方法虽然有严格的理论依据，但通常要求给出事件的先验概率和条件概率，
而这些数据又不易获得，因此使其应用受到限制。在概率论的基础上提出了一些
理论和方法，主要有可信度方法、证据理论、基于概率的贝叶斯推理方法等。

目前，在人工智能中，处理不确定性问题的主要数学工具有概率论和模糊数学。

目前常用的不确定性推理的数学方法主要有基于概率的似然推理（Plausible Reasoning）、基于模糊数学的模糊推理（FuzzyReasoning）、可信度方法，
以及使用人工神经网络算法、遗传算法的计算推理等。

1.3 基本问题

所有的不确定性推理方法都必须解决3个问题：

（1）表示问题

表示问题指的是采用什么方法描述不确定性。

在专家系统中，“知识不确定性”一般分为两类：一是规则的不确定性，二是证据的不确定性。

  • 一般用(E→H, f(H,E))来表示规则的不确定性，f(H,E)即相应规则的不确定性程度，称为规则强度。
  • 一般用(命题E, C(E))表示证据的不确定性，C(E)通常是一个数值，代表相应证据的不确定性程度，称为动态强度。

规则和证据不确定性的程度常用可信度来表示。

在专家系统MYCIN 中，可信度表示规则及证据的不确定性，取值范围为[−1, 1]。

  • 当可信度取大于零时，其数值越大，表示相应的规则或证据越接近于“真”；
  • 当可信度小于零时，其数值越小，表示相应的规则或证据越接近于“假”。

（2）语义问题

语义问题指上述表示和计算的含义是什么，即对它们进行解释。即需要对规则和证据的
不确定性给出度量。

  • 对于证据的不确定性度量C(E)，需要定义在下述3种典型情况下的取值：
    • E为真，C(E)=?
    • E为假，C(E)=?
    • 对E一无所知，C(E)=?
  • 规则的不确定性度量f(H,E)，需要定义在下述3种典型情况下的取值：
    • 若E为真，则H为真，这时f(H,E)=?
    • 若E为真，则H为假，这时f(H,E)=?
    • E对H没有影响，这时f(H,E)=?

（3）计算问题

计算问题主要指不确定性的传播和更新。即计算问题定义了一组函数，求解结论的
不确定性度量。

主要包括3方面：

  • 不确定性的传递算法
    • 已知前提E的不确定性C(E)和规则强度f(H,E)求结论H的不确定性
    • 即定义函数f1，使得C(H)=f1(C(E),f(H,E))
  • 结论不确定性合成
    • 由两个独立的证据E1和E2求得的假设H的不确定性C1(H)和C2(H)，求证据E1和E2的组合导致的假设H的不确定性
    • 即定义函数C(H)=f2(C1(H),C2(H))
  • 组合证据的不确定性算法
    • 已知证据E1和E2的不确定性C1(E)和C2(E)，求证据E1和E2的析取和合取的不确定性
    • 即定义函数C(E1∧E1)=f3(C(E1),C(E2))；C(E1∨E2)=f4(C(E1),C(E2))

组合证据的不确定性的计算已经提出了多种算法，用得最多的是如下3种：

  • 最大最小法
    • C(E1∧E2) = min{C(E1),C(E2)}
    • C(E1∨E2) = max{C(E1),C(E2)}
  • 概率方法
    • C(E1∧E2) = C(E1)×C(E2)
    • C(E1∨E2) = C(E1)+C(E2)−C(E1)×C(E2)
  • 有界方法
    • C(E1∧E2) = max{0, C(E1)+C(E2)−1}
    • C(E1∨E2) = min{1, C(E1)+C(E2)}

2. 概率方法

有完善的理论，被最早用于不确定性知识的表示和处理。但因条件概率不易给出、计算量
大等原因，应用受了限制。

2.1 基础知识

（1）条件概率定义

P(B|A)=P(AB)/P(A)称为事件A发生的条件下事件B的条件概率

（2）全概率公式

设事件A1,A2,…,An互不相容，其和为全集。则对于任何事件B：P(B)=Σ(P(Ai)×P(B|Ai))

一般的，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为
全集，通常记作U。

（3） 贝叶斯公式

设事件A1,A2,…,An互不相容，其和为全集。则对于任何事件B：
P(Ai|B)=P(Ai)×P(B|Ai)/P(B)

贝叶斯公式可以用条件概率公式证明：

推导：
P(Ai|B) = P(AiB)/P(B)         #条件概率公式
        = P(Ai)×P(B|Ai)/P(B)  #分子代入条件概率公式

证明：
P(Ai|B) = P(Ai)×P(B|Ai)/P(B)
        = P(AiB)/P(B)         #分子代入条件概率公式
        = P(Ai|B)             #条件概率公式

用全概率公式代入贝叶斯公式，可以得到贝叶斯公式的另一种形式：

P

(

A

i

∣

B

)

=

P

(

A

i

)

 

P

(

B

∣

A

i

)

Σ

i

[

P

(

A

i

)

P

(

B

∣

A

i

)

]

P(A_i|B)=\\frac{P(A_i)\\ P(B|A_i)}{\\Sigma_i [P(A_i)P(B|A_i)]}

P(Ai​∣B)=Σi​[P(Ai​)P(B∣Ai​)]P(Ai​) P(B∣Ai​)​

其中:

  • P(Ai)是事件Ai的先验概率
  • P(B|Ai)是在事件Ai发生条件下事件B的条件概率
  • P(Ai|B)是在事件B发生条件下事件Ai的后验概率。
  • 先验概率是指根据以往经验和分析得到的概率。
  • 后验概率指某件事已经发生，计算这件事发生的原因是由某个因素引起的概率(根据结果求原因的概率)。

2.2 经典概率方法

（1）单条件

  • 设有产生式规则：IF E THEN Hi (其中，E为前提条件，Hi为结论)
  • 用条件概率：P(Hi|E) 表示证据E条件下，Hi成立的确定性程度

（2）复合条件

  • 对于复合条件： E = E1 AND E2 AND … AND Em
  • 用条件概率：P(Hi|E1,E2,…,Em) 表示E1,E2,…,Em出现时，结论Hi的确定性程度

2.3 逆概率方法

在实际中，求条件E出现情况下结论Hi的条件概率P(Hi|E)非常困难。
但是求逆概率P(E|Hi)要容易的多。

比如：E 代表咳嗽，以Hi代表支气管炎

  • P(Hi|E)，咳嗽的人中有多少是患支气管炎，统计工作量较大
  • P(E|Hi)，患支气管炎的人有多少咳嗽，统计就容易多了

如果前提条件E表示，用Hi表示结论，用贝叶斯公式就可得到：

P

(

H

i

∣

E

)

=

P

(

H

i

)

 

P

(

E

∣

H

i

)

Σ

i

[

P

(

H

i

)

P

(

E

∣

H

i

)

]

P(H_i|E)=\\frac{P(H_i)\\ P(E|H_i)}{\\Sigma_i [P(H_i)P(E|H_i)]}

P(Hi​∣E)=Σi​[P(Hi​)P(E∣Hi​)]P(Hi​) P(E∣Hi​)​

当已知Hi的先验概率，结论Hi成立时E的条件概率P(E|Hi)就可以求Hi的条件概率。

多个证据E1,E2,…,Em和多个结论H1,H2,…,Hn,则可以进一步扩充为：

P

(

H

i

∣

E

1

,

E

2

,

.

.

.

,

E

m

)

=

P

(

H

i

)

P

(

E

1

∣

H

i

)

P

(

E

2

∣

H

i

)

.

.

.

P

(

E

m

∣

H

i

)

Σ

[

P

(

H

i

)

P

(

E

1

∣

H

i

)

P

(

E

2

∣

H

i

)

.

.

.

P

(

E

m

∣

H

i

)

]

P(H_i|E_1,E_2,…,E_m) = \\frac{P(H_i)P(E_1|H_i)P(E_2|H_i)…P(E_m|H_i)}{Σ[P(H_i)P(E_1|H_i)P(E_2|H_i)…P(E_m|H_i)]}

P(Hi​∣E1​,E2​,...,Em​)=Σ[P(Hi​)P(E1​∣Hi​)P(E2​∣Hi​)...P(Em​∣Hi​)]P(Hi​)P(E1​∣Hi​)P(E2​∣Hi​)...P(Em​∣Hi​)​

3. 可信度方法

可信度是指人们根据以往的经验对某个事物或现象为真的程度的一个判断，或者说是人们对某个事物或现象为真的相信程度。

3.1 可信度的基本概念

3.1.1 可信度的定义

可信度最初定义为信任与不信任的差。

CF(H,E) = MB(H,E)-MD(H,E)

CF(Certainty Factor，确定性因子)是由证据E得到假设H的可信度。

MB(Measure Belief)称为信任增长度，表示E的出现使结论H为真的信任值增长程度。

  • MB(H,E) = 1 当P(H)=1时
  • MB(H,E) =(max(P(H|E),P(H)}-P(H))/(1-P(H)) 其他情况

MD(Measure Disbelief)称为不信任增长度

  • MD(H,E)=1 当P(H)=0时
  • MD(H,E) =(min(P(H|E),P(H)}-P(H))/(-P(H)) 其他情况

根据以上定义，可以得到：

  • CF(H,E)=MB(H,E)-0 当P(H|E)>P(H)时
  • CF(H,E)=0 P(H|E)=P(H)时
  • CF(H,E)=0-MD(H,E) 当P(H|E)<P(H)时

** 3.1.2 可信度的性质**

（1）互斥性

  • 当MB(H,E)>0时， MD(H,E)=0
  • 当MD(H,E)>0时， MB(H,E)=0

（2）值域

  • 0≤MB(H,E)≤1
  • 0≤MD(H,E)≤1
  • -1≤CF(H,E)≤1

（3）典型值

  • CF(H,E)=1时，P(H|E)=1, MB(H,E)=1, MD(H,E)=0
  • CF(H,E)=-1时，P(H|E)=0, MB(H,E)=0, MD(H,E)=1
  • CF(H,E)=0时，P(H|E)=P(H)，MB(H,E)=0, MD(H,E)=0，表示E对H无影响

（4）H的信任增长度等于非H的不信任增长度

  • MB(H,E) = MD(¬H,E)
  • MD(H,E) = MB(¬H,E)

（5）H的可信度对非H的可信度之和等于0

  • CF(H,E)+CF(¬H,E) = 0

（6）可信度与概率的区别

  • 概率：P(H)+P(¬H)=1 且 0≤P(H),P(¬H)≤1
  • 可信度：-1≤CF(H,E)≤1

**（7）对于同一前提E，若支持多个不同的结论Hi，则

  • ΣCF(Hi,E) ≤1

实际应用中，P(H)和 P(H|E)的值很难获得，因此CF(H,E)的值由领域专家给出。

3.2 可信度模型

3.2.1 规则的不确定性的表示

可信度(CF)模型中，规则用产生式规则表示：

IF E THEN H (CF(H,E))

3.2.2 证据的不确定性表示

可信度(CF)模型中，证据E的不确定性也用可信度因子CF表示，取值范围为[-1,1],典型值为：

  • 证据E肯定为真: CF(E)=1
  • 证据E肯定为假: CF(E)=-1
  • 证据E一无所知: CF(E)=0

3.2.3 组合证据的不确定性的计算

  • E=E1 AND E2 AND … AND En
    • CF(E) = min({CF(E1),CF(E2),…,CF(En)}’
  • E=E1 OR E2 OR … OR En
    • CF(E) = max({CF(E1),CF(E2),…,CF(En)}

3.2.4 否定证据的不确定性计算

  • CF(¬E) = -CF(E)

3.2.5 不确定性推理

  1. 证据肯定存在，即CF(E)=1时，则CF(H)=CF(H,E)
  2. CF(E)≠1时，则CF(H)=CF(H,E)×max{0,CF(E)}
    • CF(E)＜0时，CF(H)=0
  3. 多条相互独立的规则分别推出相同结论，结论合成综合可信度算法
    • 分别对每个规则用第二步公式求出CF，即CF1(H),CF2(H)…
    • 对E1、E2求综合可信度
      • CF(H) = CF1(H)+CF2(H)-CF1(H)×CF2(H) 当CF1,CF2≥0时
      • CF(H) = CF1(H)+CF2(H)+CF1(H)×CF2(H) 当CF1,CF2<0时
      • CF(H) = CF1(H)+CF2(H) 当CF1,CF2异号时
    • 对于多条规则，依次合成，直到结束。

可信度模型的特点：

  • 简洁、直观、容易理解
  • 可能和条件概率得出的值相反、计算的累积可能导致一个规则和多个规则计算结果不同、组合规则顺序不同可能结果不同

4. 模糊推理

4.1 模糊数学的基本知识

4.1.1 模糊集合

（1）定义

集合元素对集合的隶属程度称为隶属度，用 µ 表示。

  • µ=1，表示元素属于集合
  • µ=0，表示元素不属于集合

模糊集合用“隶属度/元素”的形式来记：

A

=

µ

1

/

x

1

+

µ

2

/

x

2

+

.

.

.

+

µ

n

/

x

n

=

∫

μ

A

(

x

)

/

x

A = µ1/x1 + µ2/x2 + … + µn/xn =\\int μA(x)/x

A=µ1/x1+µ2/x2+...+µn/xn=∫μA(x)/x

（2）模糊集合相等

A=B，当且仅当：∀x，μA(x)=μB(x)

（3）模糊集合包含

B包含A，当且仅当：∀x∈U，μA(x)≤μB(x)

A,B均是论域U上的模糊集合，即A,B中的元素∈U，下同

（4）模糊集合并、交、补

  • µ(A∪B)(x) = max(µA(x), µB(x)) ∀x∈U
    • 也记为：µA(x) ∨ μB(x) ∨表示取极大
  • µ(A∩B)(x) = min(µA(x), µB(x)) ∀x∈U
    • 也记为：µA(x) ∧ μB(x) ∧表示取极小
  • µ(¬A)(x) = 1-(µA(x) ∀x∈U

（5）模糊集合的积

A、B分别是论域U、V上的模糊集合。即A中的元素为x∈U，B中的元素为y∈V

  • A×B = ∫(μA(x) ∧ μA(y))/(x,y)

相乘之后元素变为(x,y)值对

4.1.2 模糊关系及运算

（1）模糊关系定义

论域U到V上的模糊关系R：指U×V上的一个模糊集合：

  • 集合元素为有序对<x,y>
  • 集合隶属函数为μR(x,y)

模糊关系 R 通常用矩阵表示：

以U=V={1,2,3}为例：

x\\y 1 2 3
1 0 0.1 0.6
2 0 0 0.1
3 0 0 0 
模糊关系矩阵
R=[[0, 0.1, 0.6],
   [0,   0,  0.1],
   [0,   0,   0]]

（2）模糊关系的合成

  • R 是 U×V 上的模糊关系
  • S 是 V×W 上的模糊关系
  • U×W（叉积）上的模糊关系T=R৹S

模糊关系T的隶属函数为：

T=∪(μR(x,y) ∧ μS(y,z))

示例：

 R=[0.3, 0.7, 0.2]    #1x3
 S=[0.2,
    0.6,
    0.9]              #3x1
 
 T=(0.3∧0.2) ∨ (0.7∧0.6) ∨ (0.2∧0.9) = 0.6

4.2 模糊假言推理

4.2.1 模糊规则的表示

模糊命题的一般形式：x is A 或者 x is A(CF)

模糊规则产生式的一般形式： IF E THEN R(CF,λ)

  • E：用模糊命题表示的模糊条件
  • R：用模糊命题表示的模糊结论
  • CF：该产生式规则所表示的知识的可信度因子，由领域专家在给出规则时同时给出
  • λ：阈值，用于指出相应知识在什么情况下可被应用

模糊规则示例：

IF x is A THEN y is B(λ)
IF x is A THEN y is B(CF, λ)
IF x1 is A1 AND x2 is A2 THEN y is B(λ)
IF x1 is A1 AND x2 is A2 AND x3 is A3 THEN y is B(CF, λ)

4.2.2 证据的模糊匹配

规则的前提条件中的 A 与证据中的 A′ 不一定完全相同，推理时需要先考虑他们的相似程度是否大于某个预先设定的阈值λ。

贴近度是一种表示接近程度的计算方法。A,B的贴近度定义为：

(A,B) = 0.5[ A·B + (1-A⊙B) ]
其中：
A·B = ∨( μA(xi) ∧ μA(xi))
A⊙B = ∧( μA(xi) ∨ μA(xi))

“∧”表示取极小，“∨”表示取极大

4.2.3 简单模糊推理

模型：

  • IF x is A THEN y is B(λ)
  • 证据：x is A’ 且（A,A’)≥λ
  • 结论：y is B’

推理步骤：

  1. 构造A、B之间的模糊关系R
    • R的典型构造方法扎德法
  2. 合成R与前提，B’=A’৹R
  3. 得出结论

个人总结，部分内容进行了简单的处理和归纳，如有谬误，希望大家指出，持续修订更新中。

修订历史版本见：https://github.com/hustlei/AI_Learning_MindMap

© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
综合
# 人工智能导论
喜欢就支持一下吧
点赞367 分享
hustlei的头像-卡核
人工智能导论(6)——机器学习(Machine Learning)-卡核
人工智能导论(6)——机器学习(Machine Learning)
人工智能导论(6)——机器学习(Machine Learning)
1年前 9003
人工智能导论(5)——搜索策略(Search Strategy)-卡核
人工智能导论(5)——搜索策略(Search Strategy)
人工智能导论(5)——搜索策略(Search Strategy)
1年前 8614
人工智能导论(9)——自然语言处理(Natural Language Processing)-卡核
人工智能导论(9)——自然语言处理(Natural Language Processing)
人工智能导论(9)——自然语言处理(Natural Language Processing)
1年前 8404
人工智能导论(1)——人工智能概述-卡核
人工智能导论(1)——人工智能概述
人工智能导论(1)——人工智能概述
1年前 7684
人工智能导论(10)——机器人(Robot)-卡核
人工智能导论(10)——机器人(Robot)
人工智能导论(10)——机器人(Robot)
1年前 7537
人工智能导论系列目录-卡核
人工智能导论系列目录
人工智能导论系列目录
1年前 6500
相关推荐
排查软件关闭时访问了0xfeeefeee内存地址导致内存访问违例的崩溃-卡核
排查软件关闭时访问了0xfeeefeee内存地址导致内存访问违例的崩溃
排查软件关闭时访问了0xfeeefeee内存地址导致内存访问违例的崩溃
2个月前 4.4W+
引发0xC0000005内存违例几种可能原因分析-卡核
引发0xC0000005内存违例几种可能原因分析
引发0xC0000005内存违例几种可能原因分析
2个月前 4.3W+
卡核知识库-卡核
卡核知识库
卡核知识库
9个月前 4.2W+
使用chatGPT,我做了一些好玩的功能，内附免费使用chatGPT网址。-卡核
使用chatGPT,我做了一些好玩的功能，内附免费使用chatGPT网址。
使用chatGPT,我做了一些好玩的功能，内附免费使用chatGPT网址。
9个月前 4W+
Radioss干货丨一次冲击不够爽，连续加载考虑一下吗？-卡核
Radioss干货丨一次冲击不够爽，连续加载考虑一下吗？
Radioss干货丨一次冲击不够爽，连续加载考虑一下吗？
2年前 3.8W+
C++软件异常分析概述-卡核
C++软件异常分析概述
C++软件异常分析概述
4个月前 3.8W+
评论 抢沙发
头像
欢迎您留下宝贵的见解！
提交
头像

昵称

取消
昵称

请填写用户信息：

  • 昵称(必填)
  • 邮箱(必填)
表情
[aoman][baiyan][bishi][bizui][cahan][ciya][dabing][daku][deyi][doge][fadai][fanu][fendou][ganga][guzhang][haixiu][hanxiao][zuohengheng][zhuakuang][zhouma][zhemo][zhayanjian][zaijian][yun][youhengheng][yiwen][yinxian][xu][xieyanxiao][xiaoku][xiaojiujie][xia][wunai][wozuimei][weixiao][weiqu][tuosai][tu][touxiao][tiaopi][shui][se][saorao][qiudale][qinqin][qiaoda][piezui][penxue][nanguo][liulei][liuhan][lenghan][leiben][kun][kuaikule][ku][koubi][kelian][keai][jingya][jingxi][jingkong][jie][huaixiao][haqian][aini][OK][qiang][quantou][shengli][woshou][gouyin][baoquan][aixin][bangbangtang][xiaoyanger][xigua][hexie][pijiu][lanqiu][juhua][hecai][haobang][caidao][baojin][chi][dan][kulou][shuai][shouqiang][yangtuo][youling]
代码

请输入代码：

确认
图片

    暂无评论内容