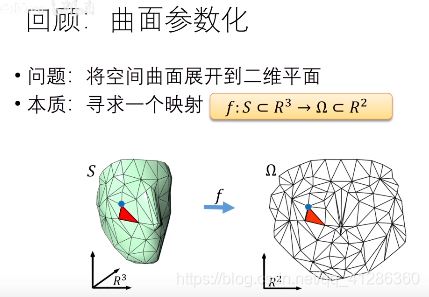
1 几何映射

1 映射表达

1 例子1

拖动一个点，其他点如何变化，本质是个插值问题。

对顶点的位置加约束，对梯度加约束

2 例子2

边界重心坐标的重新计算



不同的重心坐标其效果不一样。

2 映射的性质

双射：一一对应（Bijective）保证了没有重叠的点
局部双射–就是单射
单射
满射

翻转，非单射现象

右边没有翻转，不翻转的情况下扭曲更小是想要的
三角形有效面积是不是发生了变化，三个点是否形成了同样的右手系或者左手系

局部是双射，但是全局不是双射了。

判断具备翻转一个行列式是否发生了翻转。

判断具备翻转一个行列式的雅可比的正负是否发生了翻转。如果每个点雅可比处处都是大于零，那肯定是Bijective.

很难由局部性质转为全局性质。

本质上是个碰撞的问题.

不同的度量

3 映射的优化模型

约束一个能量，使得他满足一个条件。




如何保证三角形还连续

变量转换到ui里面了。

4 几何优化的求解

最近用的比较多的是“

2 几何映射summary

3 几何优化

建模和仿真

1 回顾

把问题变成一个数学模型后，剩下的问题就是用数学方法解它而已！

2 一些概念

1 梯度

梯度就是导数的推广，n=1就是一阶导数，n是多维就是偏导

2 Jacobian

3 Hessian

一个函数的两阶逼近 的两阶项的度量H,

4 驻点

梯度等于0的点或者导数等于零的点
拐点，

2 优化问题的类型

单目标和多目标，找个最短路，距离最近，时间最短，同时优化这两个就是多目标，这两个找个平衡点，或者两个个目标加权最后优化。

1 无约束的优化

1 梯度下降法

迭代的方法，超着最速下降法，
ak这个数值是重要，不能太大，也不能太小，太大了会导致跑的太过，大小会导致太小。

2 牛顿法

局部抛物线逼近，h非正定矩阵，它的逆矩阵很难求。所以需要用它的接近，拟合

3拟牛顿法

4 坐标下降法

优化的软件使用

2 等式约束

3 不等式约束

4 凸优化

5 其他优化

混合型优化

6 几何处理中的优化问题

4 优化相关软件

5 参考书目

目的就是找一个函数的最优化：

实际问题中，找方法和技巧

6 视频

https://www.bilibili.com/video/BV1NA411E7Yr?p=12