快速跳转:
1、矩阵变换原理Transform(旋转、位移、缩放、正交投影、透视投影)
2、光栅化(反走样、傅里叶变换、卷积)
3、着色计算(深度缓存、着色模型、着色频率)
4、纹理映射(重心坐标插值、透视投影矫正、双线性插值MipMap、环境光遮蔽AO)
5、几何(距离函数SDF、点云、贝塞尔曲线、曲面细分、曲面简化)
6、阴影映射(Shadow Mapping)
7、光线追踪原理(线面求交、预处理光追加速)
8、辐射度量学与光线追踪
9、蒙特卡洛路径追踪(Path Tracing)(光源采样)
10、材质(BRDF)(折射、菲涅尔项、微表面模型、各向异性材质)
11、渲染前沿技术介绍(双向路径追踪BDPT、MLT、光子映射、实时辐射度、外观建模)
12、相机(视场、曝光、光圈(F-Stop)、薄棱镜近似、CoC、景深)
13、光场、颜色与感知
14、动画(物理模拟、质点弹簧系统、粒子系统、运动学、动作捕捉、欧拉方法)
Lecture13~14
1 光栅化和光线追踪
光栅化:已知三角形在屏幕上的二维坐标,找出哪些像素被三角形覆盖。物体 找 像素点
光线追踪:从相机出发,对每个像素发射射线,去探测物体,判断这个像素被谁覆盖。像素点 找 物体
- 光栅化
光栅化不能很好的模拟全局光照效果
基本只考虑光线弹射一次,即从光源打到物体表面弹射到相机
是一种近似的效果,不准确、不真实 - 光线追踪的优势
更方便地处理间接光照(光线到达相机之前弹射多次)
更好实现软阴影、毛玻璃效果
准确、真实、符合物理规律、质量非常高 - 光线追踪唯一的缺点:特别慢

2 Whitted-Style光线追踪
2.1 定义图形学中光线的性质
不同于光在波动学中的定义,对于图形学中的光线简化(并不是很正确、很物理)的定义:
(1)光沿直线传播
(2)光线之间不会相互影响、碰撞
(3)光本该从光源出发照射到物体反射进入人眼,但图形学中反着来,眼睛发射光线。
2.2 光线仅弹射一次的光追
Whitted-Style光追,实际上只考虑了直接光照,即直接从光源照射到物体,然后物体反射光进入人眼。它并未考虑间接光照的影响,即别的物体反射的光打到另一个物体上再进入人眼。所以它不能很好的模拟全局光照的效果。
算法过程(眼睛发射光)
(1)通过摄像机对每一个像素发出一道射线(View Ray)
(2)射中物体,把该点直接连接到光源(Shadow Ray),判断是否在阴影中(没被挡住就不在阴影内)
(3)计算着色(Blinn Phong model)
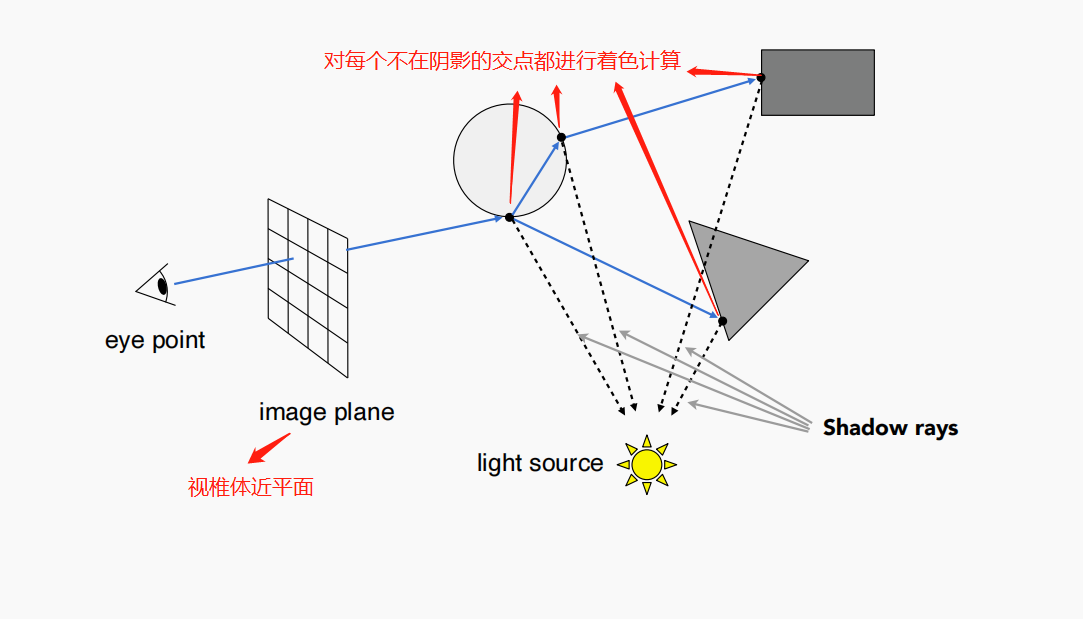
光追算法其实很好理解,摄像机(眼睛)到某像素两点一线发出射线,击中一个或多个点后,取最近一个,连到光源,若没被阻挡则不在阴影内,被阻挡则在阴影内。之后对每一个像素做一遍这个操作,有几百万个像素就要射出几百万根,所以对并行计算性能要求特别高。



如图看透明球,不仅能看到透明球,还能看到球后面的物体,这不就是光线击中球后,还进行了折射最后击中后面的地面,那交点有多个 每个交点都进行着色计算,然后按照一定的权重加到像素上

- 光线命名区分
primary ray:从摄像机射出的光线
secondary ray:反射或折射(一次或多次)后的光线
shadow rays:交点到光源的连线
3 光线-物体求交点
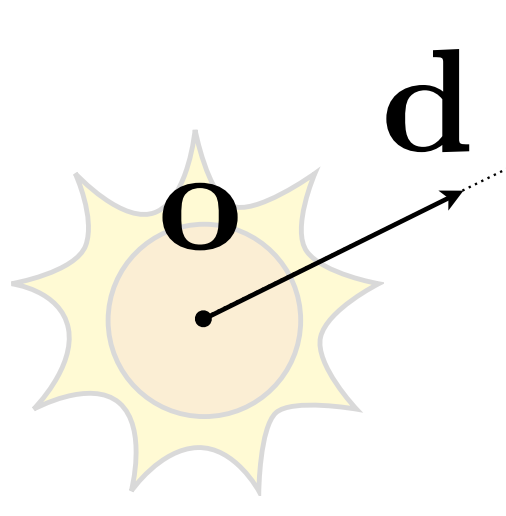
- 射线方程
定义光线:光源点、方向。t时刻光线的位置 = 光源点坐标 + t * 方向向量
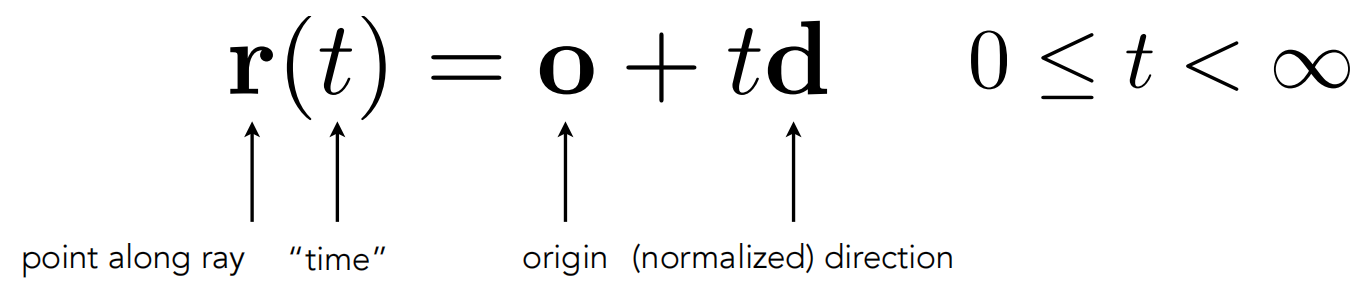
3.1 光线与球体表面
- 球体方程如下
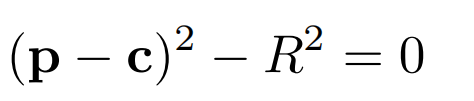
注意这个跟平常的定义不太一样(x-x0)2+(y-y0)2+(z-z0)2=R2;但其实是另一种表示而已,比如p其实就是球面上任意一点(x,y,z),c就是圆心(x0,y0,z0) 这俩相减得到一个向量,再平方(自己跟自己点积)得到的是一个标量,这个量就是R2;所以下面这个方程表示的就是位于圆心在c半径为R的球表面上的任意一点。 - 射线与球面相交与p点(已知:球心c,半径R,光源o,射线方向d)
求解过程就是解方程额
(1) o + td = p
(2) (p – c)2 – R2 = 0
把(1)带入(2)得到关于t的 一元二次方程 解之即得t,交点是p = o+td,(注意:根t必须为实数才有意义,即△ ≥ 0)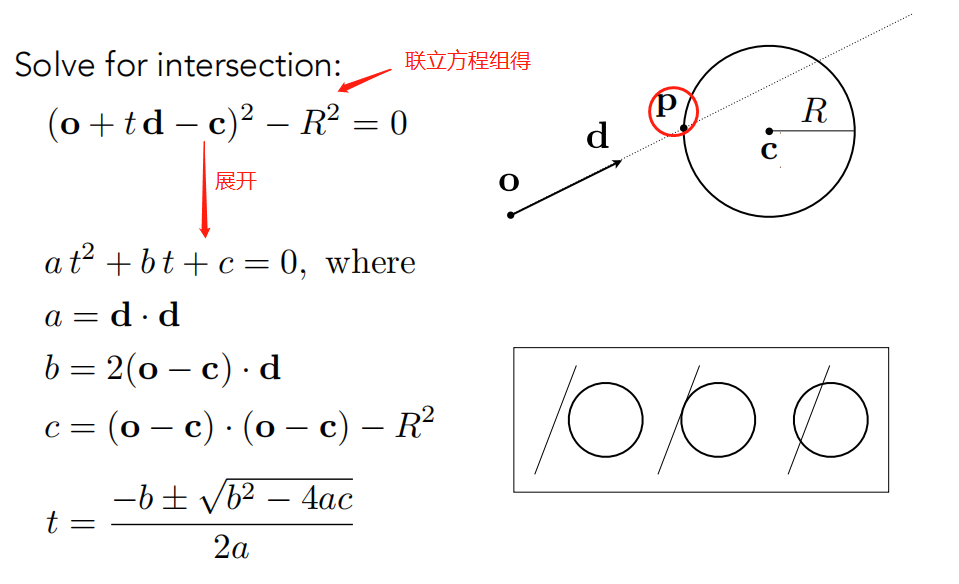
3.2 光线与隐式表面求交
解出来的是t,交点p还要o+td

3.3 光线与显式表面(三角形)求交
- 通过光线和三角形求交
渲染:可判断可见性,计算阴影、光照
几何:可判断点是否在物体内(很简单,光源发射射线,判断该射线与物体的交点有几个
奇数个交点表示在物体内,偶数个交点则在物体外) - 计算方法:遍历物体每个三角形,判断与光线是否相交
(1)光线-平面求交(三角形属于平面)
(2)计算交点是否在三角形内(3次叉乘)
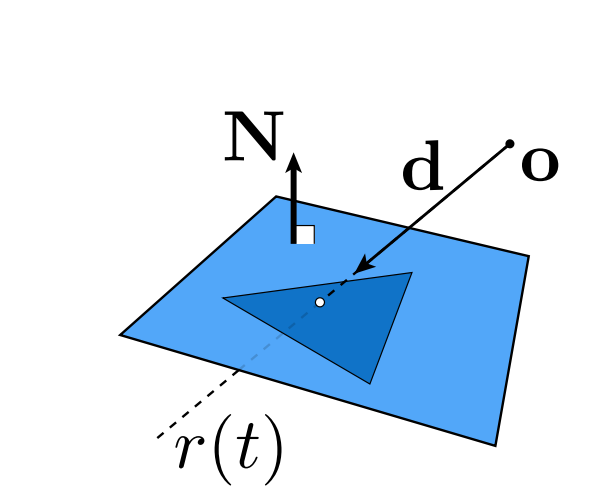
- 那么如何定义一个平面呢?
法线N+面内一个点p’(跟法线向量垂直的面有无数个,再额外给定某个点,即可唯一确定一个面)
平面方程: 平面内所有点p满足 (p – p’)·N = 0,只有p在该平面内,(p-p’)点乘N才为0,垂直嘛。
打开括号,p(x,y,z) · N(a,b,c) = ax+by+cz;然后p’ · N = d

- 然后求交点——解方程组
p = r(t) = o+td,(p – p’)·N = 0 联立这两个方程即可得到t的结果,很简单甚至没有二元一次方程了
t的右侧全都是已知量,注意验证t必须是实数
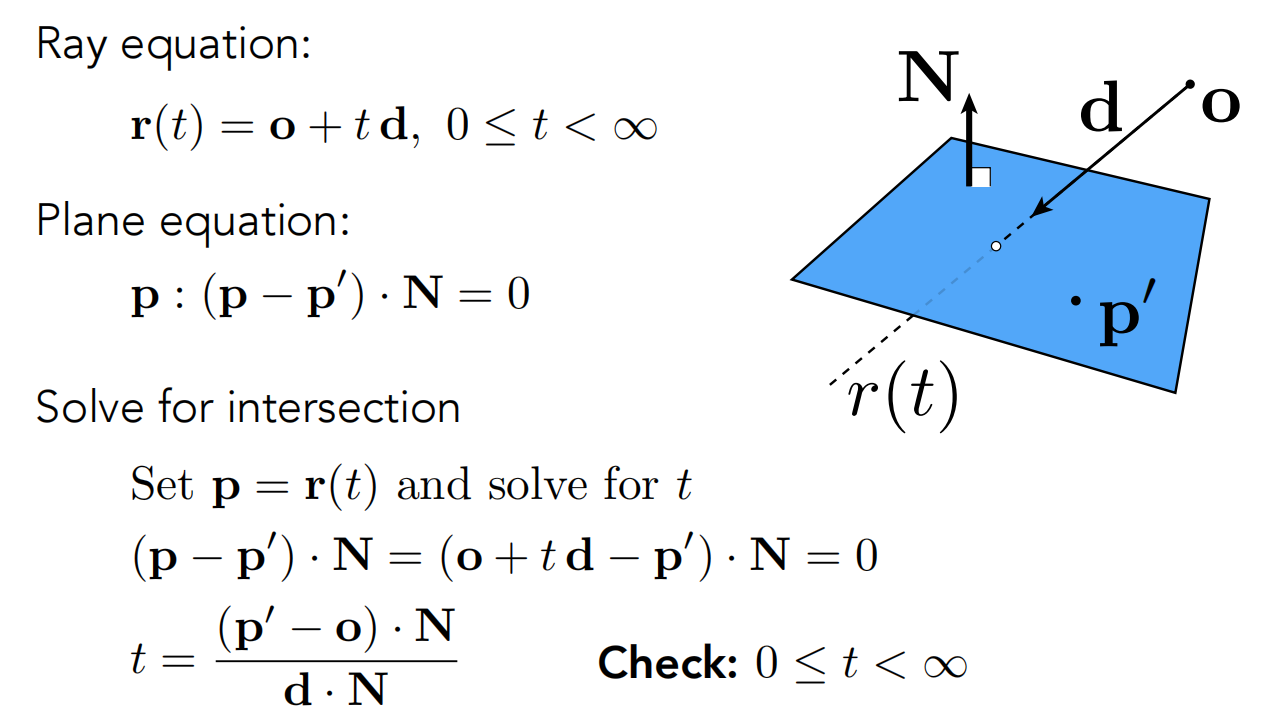
到这里只是算出t,交点= o + td,算出交点还不够(这是和平面的交点),还要满足这个点在三角形内,才能说这个点是光线和三角形的交点,即还要叉乘判断内外,结束。 - 有点麻烦啊,算这么多步骤,能不能一步到胃?——阔以
Möller-Trumbore射线-三角形求交算法
- 这种算法更方便快捷
- 他以另外一种方式描述了平面(重心坐标)
等式左边是射线(光线)方程,t是未知量
等式右边是三角形的重心坐标,P0,P1,P2是三角形三个已知顶点,b1 和 b2 是P1,P2的权重,也是交点的重心坐标的两个分量,第三个分量可以1-b1-b2算出
所以未知量一共3个 t,b1,b2
由于坐标都是三维的所以每个分量都可以对应建立1个方程,即3个未知数3个方程,可以解方程组得到3个未知量
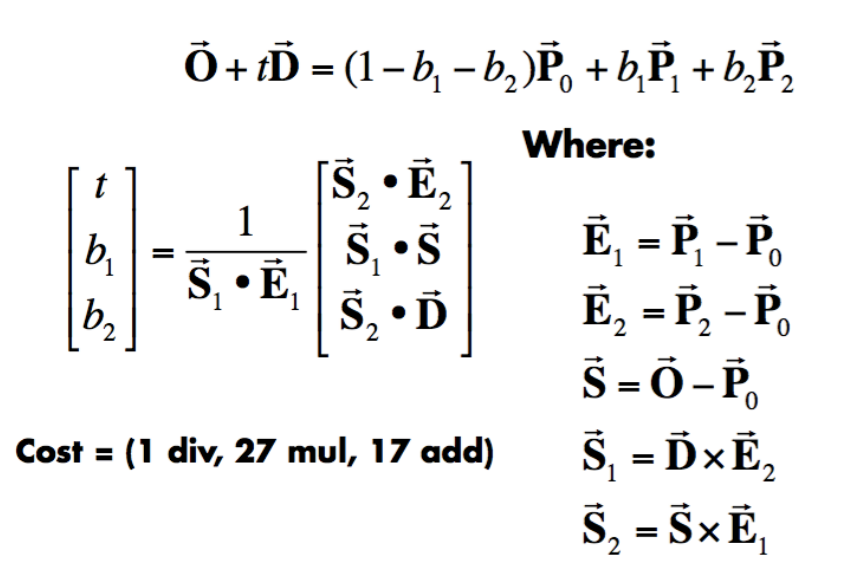
解线代方程组得到结果。要验证(t>0;b1+b2+b3 = 1,且非负)
具体推导过程
4 预处理 —— 包围盒求交加速
- 目前求交算法的花销
一根光线与场景每一个三角形都判断一次是否有交点,找到最近的击中点(通过找最小的t)。
计算次数 = 像素个数 x 场景中所有三角面个数 x 反射次数,超级慢 - 加速方法:用简单的体积包住复杂对象
场景的物体都被一个个包围盒包住,先用光线跟盒子求交,光线如果连包围盒都碰不到,里面的三角形那是必然碰不到的。
我们认为,一个盒子其实就是6个平面围住的一块公共区域,下图只画了2个平面 - 后面所有包围盒都遵循Axis-Aligned-Bounding-Box(AABB)轴对齐包围盒
轴对齐即面跟xoy或xoz或yoz任一平面平行
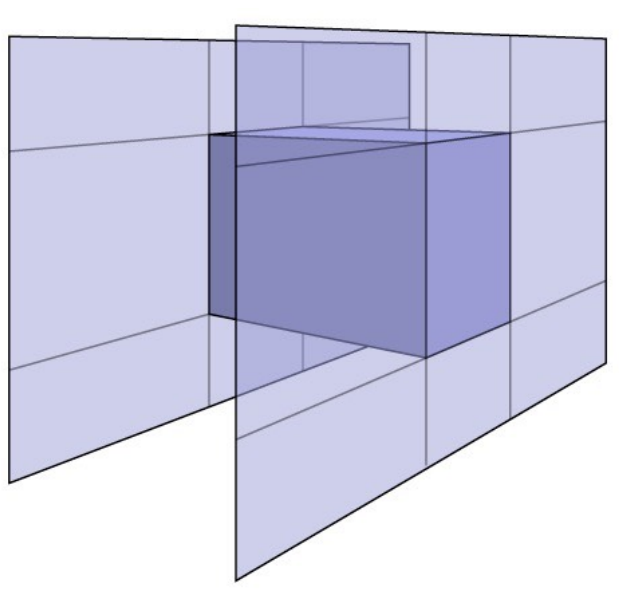
AABB(轴对齐),如何快速求交点(以与x轴对齐的面为例)?
光线方程:
p
=
o
⃗
+
t
⋅
d
⃗
\\large p=\\vec{o}+t·\\vec{d}
p=o
+t⋅d
与x轴对齐的面:
x
=
x
0
\\large x=x_0
x=x0
两者求交的方式很简单,明确目的:求 t 只要求出t就能用光线方程得到交点
仅看光线方程的x轴分量,公式可以变成
p
x
=
o
x
+
t
⋅
d
x
\\large p_x=o_x+t·d_x
px=ox+t⋅dx,三个已知量,t很容易得出
o
x
\\large o_x
ox:光线起点的x分量
d
x
\\large d_x
dx:光线的方向的x分量
p
x
\\large p_x
px:目标平面的x值

稍微整理一下
- 求光线与面
x
=
x
0
\\large x = x_0
x=x0的交点:
t
=
x
0
−
o
x
d
x
\\displaystyle \\large t=\\frac{x_0-o_x}{d_x}
t=dxx0−ox
- 求光线与面
x
=
x
1
\\large x = x_1
x=x1的交点:
t
=
x
1
−
o
x
d
x
\\displaystyle \\large t=\\frac{x_1-o_x}{d_x}
t=dxx1−ox
也可以通过物理的方式记忆这个公式,
t
t
t是时间,
x
0
−
o
x
x_0 – o_x
x0−ox是两个点之间的水平距离,
d
x
d_x
dx是水平方向的速度,时间 = 距离
÷
÷
÷速度
2D中的轴对齐盒子的求交
看着挺复杂的哈
(1)首先第一幅图是跟X0,X1两个无限大的平面求交点,得到两个相交时间tmin、tmax
(2)然后跟y0、y1面求交点得到另一对时间tmin、tmax
(3)实际上这两次求交分别得到了两个线段,再对两个线段求个交集 即得到最后一张图的跟盒子的实际交点了

- 再看3D中做法
提醒:一个盒子是3对无限大的面围的一块区域
判断进入包围盒:光线进入所有对面才算进入包围盒
判断离开包围盒:光线出任意一个对面就算离开包围盒 - 小的里面找大的,大的里面找小的,就是进入和离开盒子的时间
- 进入3D盒子的时间:tenter = max{tmin}
- 离开3D盒子的时间:texit = min{tmax}
(如果texit < 0:盒子在光线发射方向的后面,不可能有交点)
(如果texit >= 0 && tenter < 0:光源在盒子内部,必然有交点)
- 总结:有交点的判定条件 (tenter < texit && texit >= 0 )
4.1 空间网格划分
做光线追踪之前,预先构建好包围盒、网格
(1)构建包围盒
(2)构建网格
(3)网格跟物体表面求交,记录内部有物体的网格

- 做光线-场景相交计算
光线跟格子求交,如果遇到"内部有物体的"格子则需要做光线-物体求交,判断光线是否跟该物体相交,从而可以找到光线跟所有物体的交点。
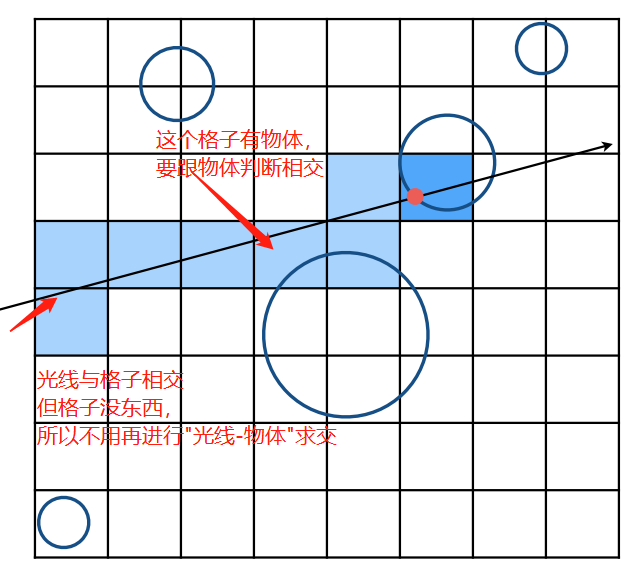
- 问题:如何知道光线首先打到哪个格子,下一次又会打到哪个格子呢?
简单的一个想法,具体算法可能与这个想法有差别:
第一个格子:可能就遍历所有格子求出一个最近的相交的格子。
下一个格子:判断光线的方向,比如向右上方发射的光线,击中某个格子后,下一个可能击中的格子必然是右边或者上面的格子,就不用遍历所有格子了。 - 其实就是光栅化一条直线,具体算法,课中未提及
- 格子的数量对于加速效果的影响?
格子太多:比像素数量还多,那你这是加速还是减速。。。
格子太少:整个世界就用一个格子,完全没有加速。
所以格子数量的多少是有讲究的。经验公式:格子数 = 对象数量 x 27 - Uniform Spatial Partitions适用的场景,物体均匀分布在场景的各个位置
4.2 非均匀空间划分
物体少的地方格子少一些,物体分布密集的地方格子多一些。
例子是2D,自己脑补3D
- Oct-Tree:类似八叉树结构,注意下面省略了一些格子的后续划分,格子内没有物体或物体足够少时,停止继续划分。
- KD-Tree:每次划分只沿着某个轴砍一刀,XYZ交替砍,不一定砍正中间,每次分出两块,类似二叉树结构。
- BSP-Tree:空间二分的方法,每次选一个方向砍一刀,不是横平竖直,所以不好求交,维度越高越难算。

- KD-Tree 预处理

注意KD-Trees有两类节点,存放的信息是不同的 - 内部节点(如ABCD)存放:
(1)对齐的轴:x、y、z的其中一个
(2)分割的位置:分裂平面沿着轴的坐标
(3)节点指针:指向两个孩子节点的指针 - 叶子节点(如12345)存放:物体对象的列表
- KD-Tree遍历

如果是内部节点则分裂、如果是叶子结点则与内部存放的对象求交


求交过程详细描述(假设KD-Tree就长上面这个样子)
光线进入盒子A触发以下逻辑
(1)判断光线与其两个子节点是否有交点
(2)孩子节点1:是叶子节点,光线与其存放的所有物体求交点
(3)孩子节点B:是内部节点,判断光线与其两个子节点是否有交点
递归,直到遍历完所有的相交的叶子结点为止。 - KD-Tree的巨大缺陷:判定物体和包围盒的交集、物体是否属于某包围盒、同一物体可能存放于多个包围盒的问题,这些问题导致KD-Tree并不受欢迎。很难去建立一个很好的KD-Tree
4.3 对象划分 Bounding Volume Hierarchy(BVH)
- 不划分空间,而是划分物体!——(换个角度思考,就美美的解决问题)
- 根节点依然是最外层大包围盒

- 逐步对物体进行分区:
(1)所有物体分成两组,对两组物体分别求一个包围盒(xyz的最值作为包围盒边界)

(2)递归,对每个包围盒内部物体重复(1)中步骤,直到包围盒中的物体足够少


BVH方法的包围盒有相交,应当尽可能减少相交量
节点细分原则
- 选择某一个轴进行划分,横平竖直
- 永远切割最长的轴,切割位置选择在物体数量的中位数附近(可以沿着该轴方向对所有三角形的中位数进行排序,找出中间的那个,复杂度o(logn);也可以不排序,快速选择算法,直接找出中间数o(n))
- 节点中的物体数量小于某个数就停止划分(比如5个)
BVH数据的存储结构
- 中间节点存放
1.包围盒
2.指向孩子节点的指针 - 叶子节点存放
1.包围盒
2.对象列表
遍历BVH的算法
遍历每个盒子的算法跟KD-Tree遍历的算法没有区别,两者只是划分盒子的角度不同
递归






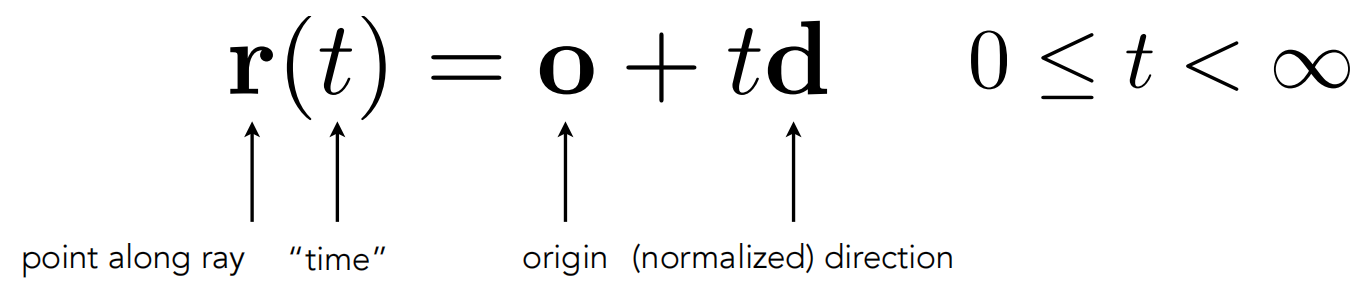
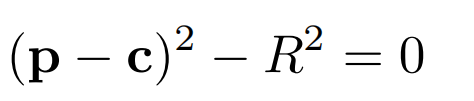



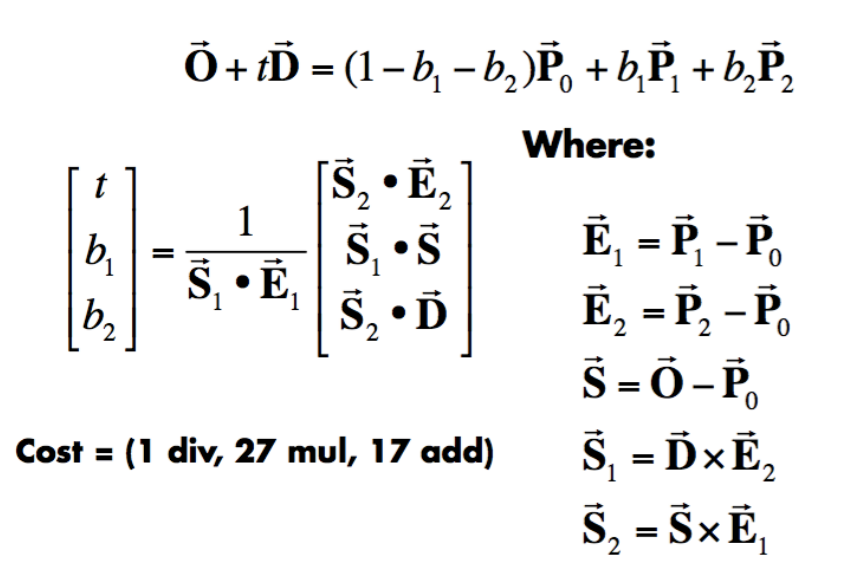










![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)










