快速跳转:
1、矩阵变换原理Transform(旋转、位移、缩放、正交投影、透视投影)
2、光栅化(反走样、傅里叶变换、卷积)
3、着色计算(深度缓存、着色模型、着色频率)
4、纹理映射(重心坐标插值、透视投影矫正、双线性插值MipMap、环境光遮蔽AO)
5、几何(距离函数SDF、点云、贝塞尔曲线、曲面细分、曲面简化)
6、阴影映射(Shadow Mapping)
7、光线追踪原理(线面求交、预处理光追加速)
8、辐射度量学与光线追踪
9、蒙特卡洛路径追踪(Path Tracing)(光源采样)
10、材质(BRDF)(折射、菲涅尔项、微表面模型、各向异性材质)
11、渲染前沿技术介绍(双向路径追踪BDPT、MLT、光子映射、实时辐射度、外观建模)
12、相机(视场、曝光、光圈(F-Stop)、薄棱镜近似、CoC、景深)
13、光场、颜色与感知
14、动画(物理模拟、质点弹簧系统、粒子系统、运动学、动作捕捉、欧拉方法)
Lec14~15
1 辐射度量学
学习辐射度量学是为得到更好的更真实的光照计算效果(Whitted光线追踪、Blinn-phong着色计算是不真实的)
辐射度量学:可以准确的测量空间中的光照的系统方法,定义了一系列属性,但是依然是在几何光学中的描述,不涉及光的波动性、互相干扰等
- Radiant Energy 辐射能Q
- Radiant Flux(Power) 辐射通量Φ
- Radiant Intensity 辐射强度I
- Irradiance 辐照度E
- Radiance 辐亮度L
学习三板斧:
why–为什么学?
what–这是个什么玩意儿?
how–怎么实现?学了就忘,所以how其实并不太重要
1.1 Radiant Energy 辐射能
定义:指电磁波中电场能量和磁场能量的总和,也叫电磁波的能量。符号:Q;单位:焦耳
图中表示意义:符号[单位]
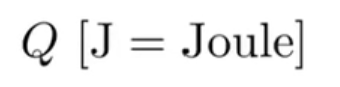
1.2 Radiant Flux(Power) 辐射通量 (辐射功率)
定义:单位时间内产生的、反射的、接收的能量。符号:Φ;单位:瓦特、流明
微分如dy/dx中的d全称为differential

1.3 Radiant Intensity 辐射强度
定义:单位立体角上,产生的、反射的、接收的辐射通量。符号:I;单位:瓦特/sr、lm/sr、candela、cd
立体角(solid angle)是有方向的,所以辐射强度是一个方向有关的属性,

1.3.1 弧度和角度
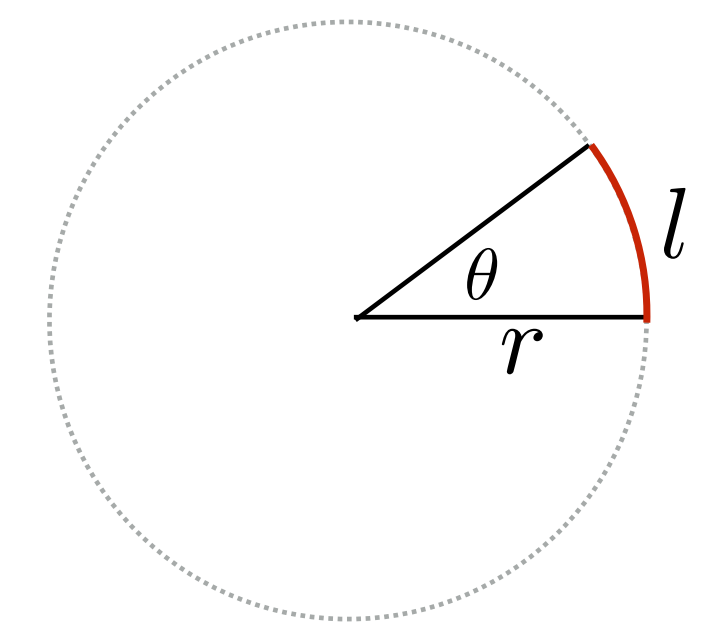
- 圆弧的弧长与半径之比, θ = l / r
圆的总的弧度(radian)为2π,对应角度为360°
1.3.2 球面度——立体角
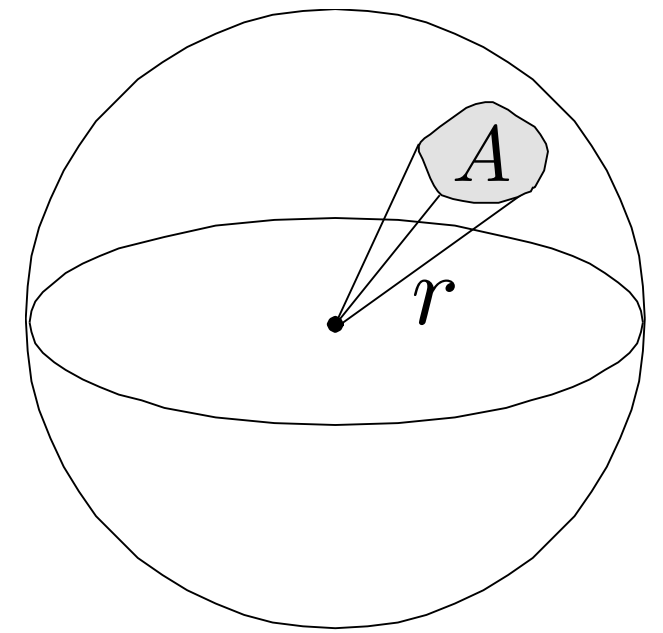
- 球面上一块面积与半径的平方之比, Ω = A / r2
球体的总的球面度(steradian)为4π = 4πr2 / r2
1.3.3 单位立体角
- 球面上单位面积与半径的平方之比,dω = dA / r2
球面的单位面积dA比较好求,求出AB和AC的弧长即可得到。根据圆的弧长公式可以得到弧长l = r · θ;
AC = r · dθ , AB = rsinθ · dφ

二重积分计算,总的立体角 = 球面上无数个单位立体角的加和,即∫∫sinθdθdφ
积分限也比较好理解:θ:0 → π,一个半圆弧, φ:0 → 2π,用半圆转一整圈得到球面

- 通常把ω当做方向向量来理解,这样比较好描述intensity
从任意一个三维空间中的方向,看向光源,光源的强度是多少,即某个方向上的光的强度

- 如果点光源向三维空间中均匀的辐射出能量,怎么描述强度?
I = Φ / 4π
Φ:点光源单位时间内,向三维空间中辐射出的能量
4π:整个三维空间的总立体角
其比值就是单位立体角上的辐射通量
1.4 Irradiance 辐照度
物体单位投影面积上接收到的能量。符号:E,单位:W/m2、lm/m2、lux
Irradiance和intensity是同级不同角度的概念,辐照度是辐射通量/面积,辐射强度是辐射通量/立体角

有了照度的定义,就可以比较好的理解曾经学过的一些知识了
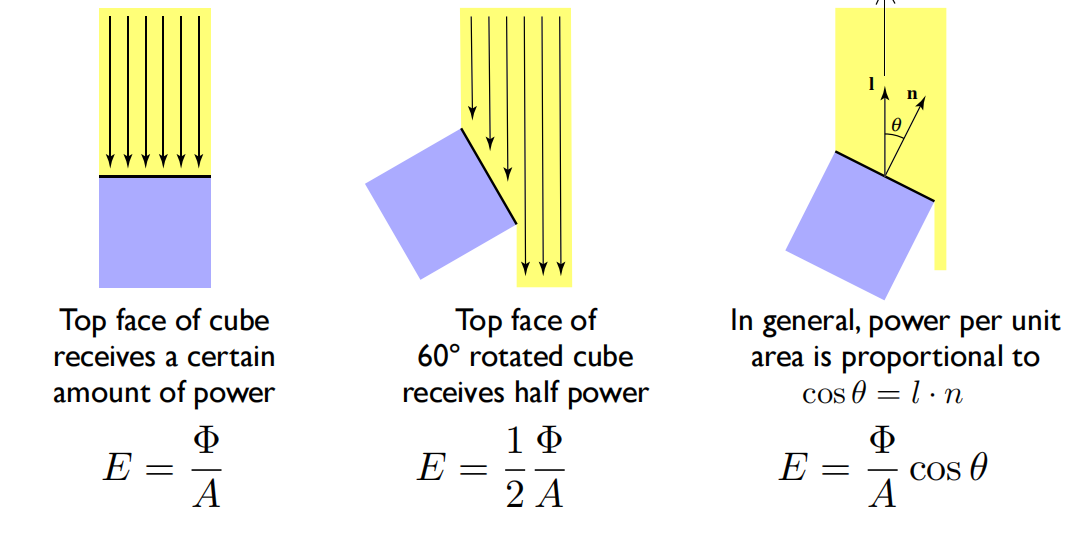
- 例一: 单位面积上接收到的能量,跟该平面的
法线和光线方向的余弦成正比
公式中的符号Φ是光源的辐射通量,A是平面的面积,其比值就是单位面积接收的辐射照度,再乘以夹角余弦,得到的就是单位投影面积的Irradiance
- 例二:地球上不同地方为何有冬夏温差之别?
北半球的某一个纬度上,光线与面法线的夹角不同
cosα > cosθ, 当地球公转到左图位置时,该纬度附近的一片区域收到的能量多,为夏季;公转到右边位置时则能量少,为冬季

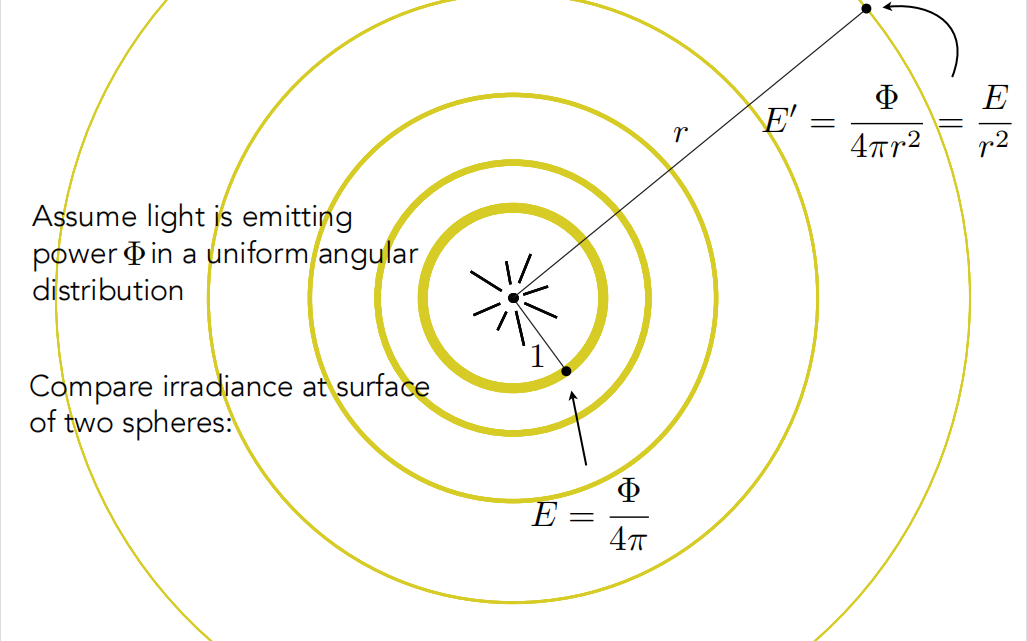
- 例三: 照度衰减。计算着色时,为何离光源越远,目标着色点接收到的能量越少呢?
单个光源下,物体上某个着色点接收到的irradiance E = Φ / S球 ,光源的能量均匀向空间中辐射,着色点的辐照度(Irradiance:某个点接受到的来自所有方向的辐射通量)只有来自该单个光源方向的辐射通量。辐射通量恒定不变,随着距离越远,辐射球的表面积却不断增大,因此球面的每个点分到的能量就少了。
Φ:辐射通量(功率),光源单位时间内辐射出的能量
S球: 球的表面积
(ps:注意衰减的是辐射球上的任意一个点所接受到的irradiance,不是intensity)
1.5 Radiance 辐亮度
描述光沿着一条线传播的属性,与路径追踪比较有关系,所以是比较重要的一个概念
定义: 单位投影面积收到/发出的单位立体角上的辐射通量、符号:L
- 根据定义就能看出,这是在辐照度的基础上某个特定的ω方向接收/发出的能量,也可以是在辐射强度的基础上某块单位面积产生/接收到的能量
dAcosθ:物体表面面积,投影到垂直于光线的平面所占面积

Radiance也能用下面两种方法求得
Radiance = irradiance per solid angle,这个后面会用
Radiance = intensity per projected unit area
intensity公式为dφ/dω
irradiance为dφ/dA


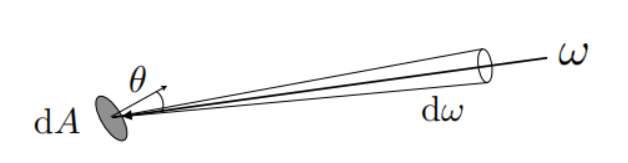
入射辐亮度incident Radiance —— 从光线接收者的角度理解Radiance
- 含义:物体表面的某单位面积上,来自某个单位立体角方向的辐射通量
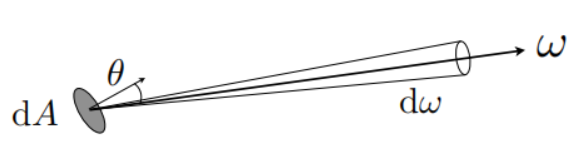
出射辐亮度Exiting Radiance —— 从光源的角度理解Radiance
- 含义:光源的单位面积上往某个单位立体角方向辐射出去的通量
注意:所有前面的属性,都可以两个角度来理解,光源或接收者
1.6 Irradiance vs. Radiance
这俩在图形学中用得特别频繁,所以务必确保搞清楚他俩的区别和联系
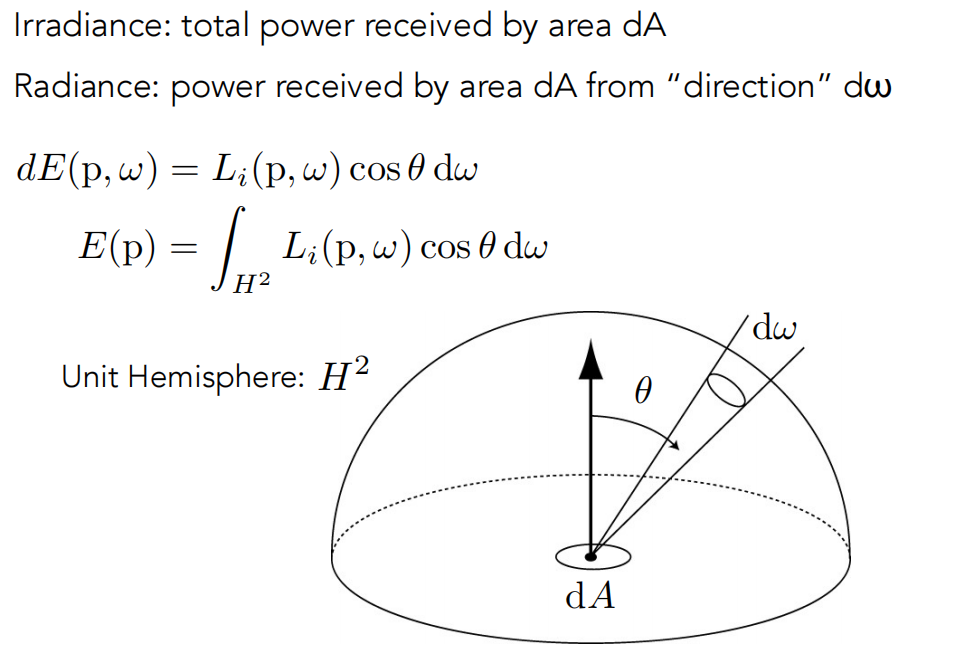
- Irradiance 辐照度: 单位面积dA接收到的通量总和
- Radiance 辐亮度: 单位面积接收到的来自dw方向的辐射通量(注意单位立体角可以认为是一个方向向量)
- 下面两个公式中的cosθ,是因为这两个属性都要求投影面积,即单位面积还要投影到与入射光垂直的面上
- 下面第一个公式其实就是 Radiance公式,不信看前面。。 下面那个就是把所有方向的Radiance加起来得到Irradiance
- 注意积分区域 H2 和 Ω2 都表示半球,因为来自下方半球的光线我们认为是背面来的光线,接收不到
2 双向反射分布函数(BRDF)
2.1 反射
反射的理解:接收到入射光后,自身变成新的光源,向空间中辐射,这样理解有助于利用Radiance和Irradiance解释反射
单位面积dA接收到 ωi 方向来的Radiance,下图中用 L(ωi) 表示,也能理解成辐照度的一个微元dE(ωi),然后再辐射到四面八方 ωr 中去,这时候辐射出去的又是Radiance(因为反射出去无数多条,power会被均分,而其中特定的一条分到的能量就是一个微元,用 dLr(x, ωr))表示

2.2 BRDF
-
双面反射分布函数 Bidirectional Reflectance Distribution Function(BRDF): 描述了入射光线经过某个表面反射后在各个可能的出射方向上能量分布(反射率)。比如已经知道入射方向 ωi 传入任意 **ωr**反射方向,能得到值域在[0,1]的浮点数返回值。返回值意义:定义某个点在 ωr 方向的反射光线的能量跟 ωi 方向射入的光线能量的比值
- 比如镜面反射,则镜面反射的方向能量接近百分之百,其他反射方向接近0
- 比如漫反射,则所有方向的能量比例相同,均分
-
BRDF是定义光线在不透明表面反射的四元函数,基本式为f(ωi,ωr) ,ωi 指光线的入射方向, ωr 指光线反射的方向,除此之外,还有一个N代表法线。每一个方向ω可以被参数化为方位角φ和天顶角θ,因此BRDF是一个四维函数。 BRDF的单位是 1/sr, sr是球面度的单位
-
就是BRDF项定义了物体不同的材质
换句话说,BRDF就是物体的材质在数学中的表达方式。
怎么理解?—— 如果我想要定义很光滑的金属材质(只发生镜面反射),那么我就把BRDF设置成镜面反射方向100%,其他方向为0; 如果我想定义一个石膏材质(只发生漫反射),则BRDF设置成所有方向都均等的,比如0.001。

3 反射方程
我们把出射方向固定到相机方向,那么每一个入射方向对应一个BRDF项,把这所有的入射方向的强度,乘以BRDF后得到的出射方向的强度加起来,作为最终反射强度。反射方程如下
fr(p,ωi → ωr): BRDF项,返回值值域[0,1]
Li(p,ωi)cosθidωi: 相乘的结果其实是dE(p, ωi)——单位面积收到的irradiance,仅考虑一条入射光
最后做个积分,把半球上每个入射光的在Lr方向的贡献全部加起来,就得到最终的结果,即此着色点在所有可能的入射光下,反射给相机看到的光亮度是什么样的。

提醒:入射光不止来自光源,也可能是其他物体反射的光。递归思想,反射出去的光Lr也可被当做其他物体的入射光Li。如果只考虑光线弹射一次,那么Li只能是光源,不止一次那就不一定是光源了。
4 渲染方程Rendering Equation
反射方程没考虑物体自发光的特性
渲染方程就更一般的考虑了自发光,增加一项物体自发光Le,并且把方程写得比较一般化,其实就只是多了个自发光
虽然入射光是从外向内的,但是我们规定入射方向的表示都是向外的(类似于之前着色计算的方向规定)
(新补充关键点:其实积分部分就是求半球上的所有方向的照度微元dE(ωi)之和,即 ∫ fr dE(ωi) ,其中照度微元又能用辐亮度式子替换掉,即dE(ωi) = Li cosθdωi)

更深入理解渲染方程,推导过程
- 如果只有一个光源,则渲染方程写出来是这样

- 多个点光源

- 面光源
点光源是把所有点光源的反射贡献加起来,面光源其实就是一堆点光源的集合,直接求积分则可算出整个面光源的能量

- 间接光
来自别的物体反射过来的光,把该物体当做一个光源,Li项变成该物体的Lr,但Lr是向外指向X着色点的,对其取反操作一下

将渲染方程简写成积分方程
- 把积分号内的已知量归到一项之中

- 再进一步简化成几个记号表示
这是算子法,就是把一系列的运算抽象成一个符号表示,它允许一个函数接收另一个函数的返回值,这样比较好进行迭代计算
最终方程就变成了,出射方向的强度 = 自发光强度 + K· 入射光强度,K直接理解成一个反射操作符

- 写成算子的形式方便级数展开
- 展开的公式为下面这个,对应的把x换成K,1换成单位矩阵I

则可以得到,用一种逼近的方式得到最终的Lr,项数(反射次数)越多,则越接近真实

最终就可以描述光线追踪了
注意哈自发光的物体本身其实就是光源,所以弹射0次相当于直接看向光源

光栅化的着色计算其实就是弹射1次,只有直接光照的结果,不考虑间接光照

所以,为什么要用光线追踪呢?
因为它可以很容易的计算出间接光照的部分
5 全局光照
全局光照(Global illumination,)(gi):既考虑场景中来自光源的直接光照,又考虑经过场景中其他物体反射后的间接光照
全局光照 = 直接光照(Direct Light) + 间接光照(Indirect Light)
课中展示的案例图,应用渲染方程
- 弹射1次,只考虑直接光照
摄像机发射光线到某个点,反射1次到光源,中间若没有阻挡,则有颜色,被阻挡了则处于阴影中,纯黑

- 弹射2次,即1次间接光照,也就是考虑全局光照

- 弹射3次,2次间接光照弹射

还可以弹射几十次的,反正画面会越来越好,越来越亮,收敛于某一个亮度
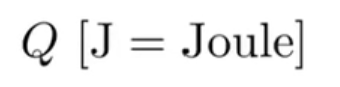
















![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)








暂无评论内容