本博客是慕课-全国大学生数学建模竞赛组委会开设的建模竞赛课学习笔记

1 数学模型分类

（1）数理型：统计回归
（2）机理型：

2 马尔萨斯人口论的引入

群体增长的趋势是什么
（1）基本论题
人类食物供给增长趋势无法跟上人口增长的趋势
（2）论证方式
公理化
（3）基本公理
• 食物为人类生存所必需
• 两性之间的情欲是必然，而且几乎会保持现状
（3）增长理论
人口有几何增长的趋势，如报数
1、2、4 、8、16。。。
食物供应只有算数增长的趋势（即是按现行函数增长的趋势）如报数
1、2、3、4、5、6。。。
人类会有无限增长的趋势，直至食物供应的极限为止
结论： 要控制人口的无节制增长
（4）马尔萨斯问题
P(t)时候的人口数量。
•

已

知

当

前

或

过

去

某

个

时

刻

的

人

口

数

量

，

预

测

未

来

某

个

时

刻

的

人

口

？

\\color{red}{已知当前或过去某个时刻的人口数量，预测未来某个时刻的人口？}

已知当前或过去某个时刻的人口数量，预测未来某个时刻的人口？
•

汉

字

格

式

遥

远

未

来

的

趋

势

（

t

趋

于

无

穷

）

？

\\color{red}{汉字格式遥远未来的趋势（t趋于无穷）？}

汉字格式遥远未来的趋势（t趋于无穷）？
解：以下是早期的马尔萨斯的模型解法。当问题随着世界的变化，各种因素的需要考虑进去，后面还有改进的马尔萨斯模型如logistic模型、lesile模型，甚至还有更复杂的模型去解决这类问题。
假如2002年和人口总数量是怕p，则2002年刚出生的人数和死亡的人数就分别是bp和dp，所以2003年初的人口总数将是
p+bp-dp = （1+b-d）p = (1+r)p
这里的r就是人口自然增长率，这个模型是离散的。
P（t+

Δ

\\Delta

Δt） – P（t） = rP(t)

Δ

\\Delta

Δt
P（t+dt） – P（t） = rP(t)dt
得到以下的微分模型

d

P

(

t

)

d

t

=

r

P

(

t

)

\\frac{dP(t)}{dt} = rP(t)

dtdP(t)​=rP(t)
P(t0) = P0
得到人口指数模型
P(t) = P₀e^r(t-t0)

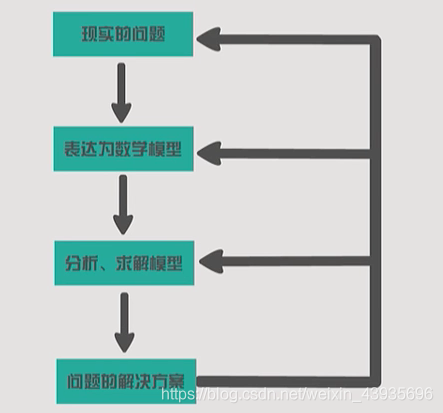
一个问题的思考方式

3 Logistic模型

d

P

(

t

)

d

t

=

r

P

(

t

)

\\frac{dP(t)}{dt} = rP(t)

dtdP(t)​=rP(t)
P(t0) = P0
（1）以上的r再当下已经不是一个常数了，是一个函数且和当前人口量相关。
r（t） = r（P（t））
改进公式
r（t） = r（P（t）） =

r

(

1

−

P

(

t

)

K

)

r(1-\\frac{P(t)}{K})

r(1−KP(t)​)
P(t0) = P0
Logistic模型

（2）Logistic模型离散化

d

N

d

t

=

r

N

(

1

−

N

K

)

\\frac{dN}{dt} = rN(1-\\frac{N}{K})

dtdN​=rN(1−KN​)

d

P

(

t

)

d

t

=

r

P

(

t

)

\\frac{dP(t)}{dt} = rP(t)

dtdP(t)​=rP(t)
考虑这个模型的离散化

Δ

N

Δ

t

=

r

N

(

1

−

N

K

)

\\frac{\\Delta N}{\\Delta t} = rN(1-\\frac{N}{K})

ΔtΔN​=rN(1−KN​)
变成了差分方程
令

Δ

N

=

N

（

t

+

1

）

−

N

（

t

）

\\Delta N = N（t+1） -N（t）

ΔN=N（t+1）−N（t）

Δ

t

=

1

\\Delta t = 1

Δt=1

N

（

t

+

1

）

−

N

(

t

)

=

r

N

(

1

−

N

K

)

N（t+1） – N(t) = rN(1-\\frac{N}{K})

N（t+1）−N(t)=rN(1−KN​)

这里的时间离散长取为1，每一代就是一个时间步

N

（

t

）

=

（

1

+

r

）

N

(

t

)

−

r

K

)

N

2

(

t

)

N（t）= （1+r）N(t) – \\frac{r}{K})N^2(t)

N（t）=（1+r）N(t)−Kr​)N2(t)
取定参数K，考虑不同的参数r
r = 1.9

r = 2.2

r = 2.5

r = 2.55

r不断的增大，周期不断的翻倍。出现倍周期现象。

4 Lesile模型

（1）概念
当人口总量一样，分布不一样的时候，以上的模型是不足以分析的。还有一个年龄的分布。
引入一个向量表示年龄分布，N(t) = [n0 n1 … ns]。把年龄分为多少段，就有多少参数。
所以当求某个t时刻的人口数量，计算公式如下图：

假设知道Lj矩阵的特征值和特征向量。

那每个时刻的N一定可以用特征向量的线性组合表示。

假设首特征值大于所有的特征值

首特征值的阿晓和相应的特征向量决定了模型的渐进性质。当首特征值大于1时候，那人口会越长越多，当小于1时，人类会走向灭亡。当等于1时，会进入一个稳态。
（2）一个学者说
所有的模型都是错的，但有些是有用的。模型越来越复杂，是一个不得已的选择。

5 更复杂的模型

（1）引入新的函数，既有t的函数又是年龄a的函数，称为多元函数P(a,t)。也是二元函数

（2）考虑其他因素
比如地域因素。或者其他确定的因素，那就要使用随机模型。推荐的书，包含了各种数学模型。