1 常用数值计算方法

（1）解线性方程组的直接方法
• 高斯消去法（Gauss）
• 三角分解追赶法
• Jacobi迭代法
• Gauss-Seidel迭代法
• 超松弛迭代法
（2）非线性方程的求根方法
• 二分法
• Newton迭代法
• 弦截法
• 抛物线法
（3）数值积分求解

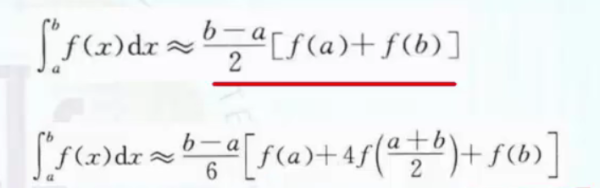
（4）数值微分求解

（5）常微分方程的数值求解
• Euler公式
• 后退的Euler法
• 改进的Euler法
• Runge-Kutta法
（6）插值法
• Lagrange一次插值法
• Lagrange插值多项式
• Newton插值
• Hermite插值
• 三次样

2 现代智能计算方法

2.1 分类

• 模拟退火算法
• 遗传算法
• 禁忌搜索算法
• 人工神经网络
• 粒子群算法
• 深度学习

2.2 遗传算法

（1）流程图

（2）核心要素
• 参数编码
• 初始种群的设定
• 适应度函数的设计
• 遗传操作设计
• 控制参数设定

2.3 神经网络

3 科技计算软件

（1）MATLAB
（2）Lingo：数学规划用得较多
（3）Spss：统计计算软件
（4）Ansys：偏微分
（5）Python：深度学习

4 习题

1. 设计一个三角追赶法函数，求解问题L*Ux = b,要求输入L、U和b，输出x

function x = fun(L,U,b) 
U = L.*U
n = size(U) % n为系数矩阵的行数
a(1)  = U(1,1)
d(1) = 0
for i=2:n-1
    a(1) = U(i,i-1)
    d(i) = U(i,i-1)
    c(i) = U(i,i+1)
end
a(n) = U(n,n)
d(n) = U(n,n-1)
c(n) = 0
t(1) = a(1) %开始求解L，U
m(1) = 0
for i=2 : n
    m(i) = b(i) %求得m(i)
    u(i-1) = c(i-1)/t(i-1)% 求得u(i)
    t(i) = a(i) - d(i) *u(i-1)% 求得t(i)
end
u(n)=0
y(1) = b(1)/t(1);
for i =2:n
    y(i) = [b(i)-m(i)*y(i-1)]/t(i);求得y(i)
end
x(n) = y(n)
for i=n-1:-1:1
    x(i) = y(i) - u(i)*x(i+1)
end
x =x'

2. 二分法求解非线性方程根的程序

function[x_star,index,it]=bisect(fun,a,b)
%求解非线性计算方程的二分法，其中，fun(x)为需要求根的函数;
%a,b为初始区间的端点;
%ep为精度，当(b-a)/2<ep时，算法能终止计算，
%缺省值为1e-5;
%当x_star迭代成功时，输出方程的根
%当x_start迭代失败时，输出两端点的值；
%index为指标变量，当index=1时，表明迭代成功，
%当index=0时，表明初始区间不是有根区间；
%it为迭代次数
if nargin<4
    ep=1e-5;
end
fa=feval(fun,a);fb=feval(fun,b);
if fa*fb>0
    x_star=[fa,fb];index=0;it=0;
    return;
end
k=1;
while abs(b-a)/2>=ep
    x=(a+b)/2;fx=feval(fun,x);
    if fx*fa<0
        b=x;fb=fx;
    else
        a=x;fa=fx;
    end
    k=k+1;
end
x_star=(a+b)/2;index=1;it=k;