1 思路

（1）背景补充
DRGs(Diagnosis Related Groups)中文翻译为（疾病）诊断相关分类，它根据病人的年龄、性别、住院天数、临床诊断、病症、手术、疾病严重程度，合并症与并发症及转归等因素把病人分入500-600 个诊断相关组，然后决定应该给医院多少补偿。

DRGs 是当今世界公认的比较先进的支付方式之一。DRGs的指导思想是：通过统一的疾病诊断分类定额支付标准的制定，达到医疗资源利用标准化。有助于激励医院加强医疗质量管理，迫使医院为获得利润主动降低成本，缩短住院天数，减少诱导性医疗费用支付，有利于费用控制。

DRGs的分组原则：

（1）逐层细化、大类概括；
（2）疾病诊断、手术或操作临床过程相似，资源消耗相近；
（3）临床经验与数据验证相结合；
（4）兼顾医保支付的管理要求和医疗服务的实际需要。 DRG 分组采用病例组合思想，疾病类型不同，应该通过诊断区分开；同类病例但治疗方式不同，亦应通过操作区分开；同类病例同类治疗方式，但病例个体特征不同，还应该通过年龄、并发症与合并症、出生体重等因素区分开，最终形成 DRG 组。

DRGs的分组思路为：

（1）以病案首页的主要诊断为依据，以解剖和生理系统为主要分类特征，参照 ICD-10 将病例分为主要诊断大类（Major diagnostic categories，MDC）。
（2）在各大类下，再根据治疗方式将病例分为“手术”、“非手术” 和“操作”三类，并在各类下将主要诊断和或主要操作相同的病例合并成核心疾病诊断相关组（ADRG），在这部分分类过程中，主要以临床经验分类为主，考虑临床相似性，统计分析作为辅助。
（3）综合考虑病例的其他个体特征、合并症和并发症，将相近的诊断相关分组细分为诊断相关组，即 DRG，这一过程中，主要以统计分析寻找分类节点，考虑资源消耗的相似性。

在DRGs分组体系中， CHS-DRG 病组的代码由 4 位码构成，均以英文 A-Z 和阿拉伯数字 0-9 表示。DRG 代码各位编码的具体含义如下：第一位表示主要诊断大类（MDC），根据病案首页的主要诊断确定，进入相应疾病主要诊断大类，用英文字母 A-Z 表示；第二位表示 DRG 病组的类型，根据处理方式不同分为外科部分、非手术室操作部分（接受特殊检查，如导管、内窥镜检查等）和内科部分，用英文字母表示。其中 A-J 共 10 个字母表示外科部分，K-Q 共 7 个字母表示非手术室操作部分；R-Z 共 9 个字母表示内科部分；病例主要诊断大类主要诊断主要诊断主要操作内科 ADRG 非手术室操作 ADRG 外科 ADRG 考虑病例的其他个体特征（年龄、合并症和并发症）进行细分组内科 DRG 非手术室操作 DRG 外科 DRG DRG 分组临床经验为主，统计分析统计分析为主，临床经验 14 第三位表示 ADRG 的顺序码，用阿拉伯数字 1-9 表示；第四位表示是否有合并症和并发症或年龄、转归等特殊情况。用阿拉伯数字表示。其中“1”表示伴有严重并发症与合并症；“3”表示表示伴有一般并发症与合并症；“5”表示不伴有并发症与合并症；“7”表示死亡或转院；“9”表示未作区分的情况；“0”表示小于 17 岁组；其他数字表示其他需单独分组的情况。

总结：

DRGS是细分后的最终的分组，DRGS编码是一个四位数的编码
DRG分组，是DRGS的上一级，还不是最细的分组
ADRG编码是DRG组的编码，是DRGS编码的前三位

（2）思路分析
通过数据分析，发现，各个ADRG组中，费用分布都有高有底，各组之间并没有高低之分。
比如BU1的费用区间是【1414.0, 144079.32】，GR1的费用区间是【107.9，214868.54】，都是由交集的。
而且通过ADRG费用的箱线图知道，整体分布式没有规律的。如果用多元线性回归去做回归预测，并不能得到什么线性或非线性的关系。
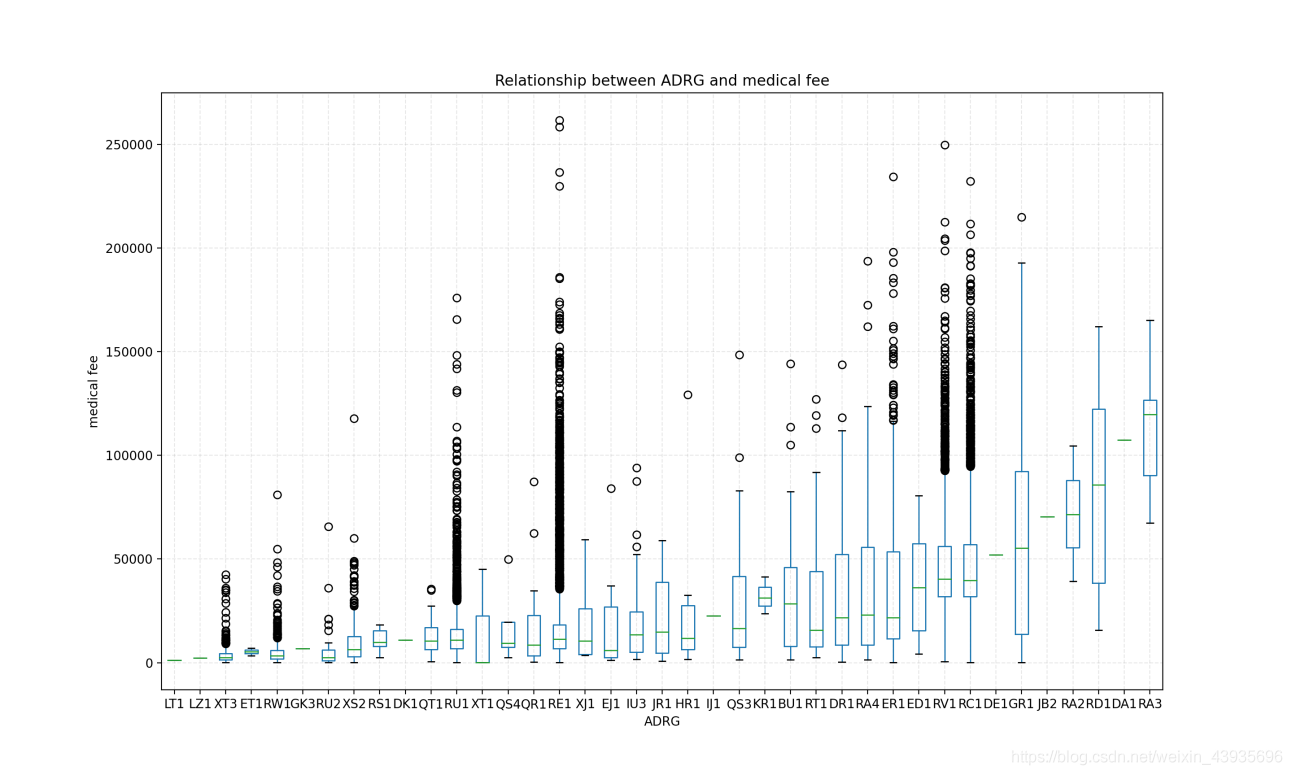
在这里插入图片描述

所以，本人大胆提出了一种想法。结合DRGS分组原则，建立这个分组原则的原因就是为了更好的归类疾病并估计费用，正好利用该规则。把ADRG组分为三个类别，每个类别都用一个平均值代替预测费用，这样预测的费用一定会有很大误差，但是在未知具体收费标准的情况下，能预测出一个大概的费用区间，就是成功的。

2 模型实现

在这里插入图片描述

def decision_tree(X,Y):
    
    X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0) 
    clf = tree.DecisionTreeClassifier()
    clf = clf.fit(X_train, y_train)
    # 模型预测
    y_pred = clf.predict(X_test)
    # 计算准确率
    score = accuracy_score(y_test, y_pred)
    print(score)
    classes = [1,2,3]
    # 获取混淆矩阵
    cm = confusion_matrix(y_test, y_pred)
    plot_confusion_matrix(cm,classes, 'confusion_matrix.png', title='confusion matrix')
    print()
    fn=['是否手术','ADRG','并发症']
    cn=['低','中', '高']
    # fig, axes = plt.subplots(nrows = 1,ncols = 1,figsize = (4,4), dpi=300)
    # tree.plot_tree(clf,
    #             feature_names = fn, 
    #             class_names=cn,
    #             filled = True)
    # 决策树可视化
    # fig.savefig('imagename.png')
    # dot_data = tree.export_graphviz(clf,
    #             feature_names = fn, 
    #             class_names=cn,
    #             out_file=None)
    # graph = pydotplus.graph_from_dot_data(dot_data)
    # graph.write_pdf('iris.pdf')
    print()
if __name__ =="__main__":
    # 读取清洗后的数据
    train_data_file = './clear_data.csv'
    t_data = pd.read_csv(train_data_file)#, names=['id', 'sex','born','intime','outtime','maindiag','elsediag','surgery','fee','days','drgsid','drgs','adrgid','adrg','highfee'])
    # 数据标准化
    sc = StandardScaler()
    data = pd.read_csv('main_label3.csv',index_col=None)
    X_i = data[['surgery','adrgid','complication']]
    sc.fit(X_i)
    X = sc.transform(X_i)
    Y = data['label']
    decision_tree(X,Y)

3 模型分析

是训练集中每组ADRG中费用分布比例是2:5:3和2:4:4的模型测试混淆矩阵，在左图中，类别为1的最多，类别3样本最少，类别1判断出错的数量占比是(24+1)/(24+1+3150) = 0.7%，类别2判断数量占比是(304)/(304+46) =86.8%，类别3判断错误的数量占比是(14+5)/(14+5+1)=95%，最终分类准确率为90.18%。类别1判断出错的数量占比是(3+2)/(3+2+3359) = 0.1%，类别2判断数量占比是(159+1)/(159+1+1) =99.3%，类别3判断错误的数量占比是(17)/(17+3)=85%，右图预测准确率达到94.78%，当比例为4:4:2时，模型准确率只有79.63%，所以在高、中、低划分比例为2：4：4，符合费用分布时该模型预测效果最佳。
在这里插入图片描述