——————————————————————————————————————————————————————————————————————–
第四讲 矩阵A的LU分解
一. 矩阵A的LU分解
在第二章中讲到了矩阵消元以及矩阵的形式的消元,消元的目的,只是为了更好的正确认识矩阵的概念,A=LU 是最基础的矩阵分解。L 是下三角矩阵,U 是上三角矩阵。A通过消元最终得到U,L 即 A 与 U 之间的联系。
1.1 A=LU的基本操作
先看 A 矩阵通过初等矩阵消元得到 U:
![图片[1]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130111-6395d4976cfd5.jpg)
这里要求的是 A=LU,L 和消元矩阵 E 是什么联系呢?L 与 E 互为逆矩阵。消元矩阵的逆是比较容易求的
![图片[2]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130113-6395d4993c7ca.jpg)
注(在参考教材中标注以下2点):
1. Every inverse matrix E^(-1) is lower triangular. Its off-diagnonal entry is l_(ij), to undo the subtraction by -l_(ij).
2. The lower triangular product of inverses is L.
1.2. A=LDU分解
有时我们将 U 中的主元提取出来,其余的位置设为 0,即 diagonal 对角阵D,可分解得到 LDU,两边各一个三角矩阵,中间一个对角阵。
![图片[3]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130114-6395d49a41194.jpg)
(LDU)
假设在三维矩阵中,消元步骤中不需要任何行交换,L 是各消元矩阵的逆的反向乘积。
1.3 LU分解中L的求解
L是:

为什么要用逆的形式?即上图中为什么下面的逆的形式的等式要比上面的等式要好?
举下面的例子,两个消元矩阵 E_21(行 2 减去 2 倍行 1)和 E_32(行 3 减去 5 倍的新行 2)相乘得新的右侧消元矩阵,那么,从右侧结果显示,元素 10 是我们不喜欢的(但它确实是运算结果),E_21(行 2 减去 2 倍行 1)和E_32(行 3 减去 5 倍的新行 2)这种顺序,行 1(元素 10)怎么就影响到了行 3 呢?这是因为,第一步中有 2 倍行 1 从行 2 中减去了,然后在第二步中又乘 5 倍从行 3 中减去,因此总共在行 3中加上了 10 倍行 1。因此,这种形式不是我们喜欢的,但逆的乘积则不是这样的。
![图片[4]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130116-6395d49c26c65.jpg)
该矩阵通过以上所描述的进行变换,第一步第二行有:3-2*1 4-2*2 1-2*0
最终第二步第三行有:5-5*(3-2*1) 0-5*(4-2*2) 5-5*(1-2*0)
即:5-5*(3-2*1) 0-5*(4-2*2) 5-5*(1-2*0)= 5-5*3+10*1 0-5*4+10*2 5-5*1+10*0
由这个结果不难看出“总共在行 3 中加上了 10 倍行 1”的结论了。
现在我们反向计算,顺序倒过来求逆的积。L 中矩阵相乘的顺序非常好,2 和 5 不会冲突,不会得到 10。
即要求出 L,不需要任何运算,只需要把所有消元乘数都写进来,就能得到 L。
![图片[5]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130116-6395d49ce6377.jpg)
总结下:A=LU,如果不存在行互换,消元乘数,即消元步骤中的需要乘以并减去的那个倍数,消元乘数可以直接写入L中。即只要步骤正确,可以在得到LU 过程中把A 抛开。例如,当你完成A 第二行的消元时,为了得到LU,你只需要记住U 中新的第二行是什么,同时消元所用的乘数也需要记住,至于A 是什么不需要管。
二. 消元与解决Ax=b耗费次数
2.1 运用A=LU来求解Ax=b
此处视频没有讲,参考书中写到了这一个问题,可以分为两个步骤:
1. Factor(intoLandU,by elimination on the left side matrixA);
2. Solve (forward elomination on b usingL, then back substitution forx usingU).
then using Forward and backward SolveLc=band then solveUx=c.
2.2 消元耗费次数
消元共耗费了多少次?A 变成 U把消元中的一次加和乘操作看为“一次”操作。100*100 的矩阵,第一主元的消元需要接近 100*100 的操作(第一行不变),第二主元的消元需要接近 99*99 的操作(第二行不变)。。。。因此 n 维矩阵的消元一共需要次数接近1/3 (N^3),1/3 是考虑到求和式子中数字在逐渐减小,如果不减小的话应该是n*(n^2),这才是n^3。这其中有微积分的知识:从 1 到 n 对 (x^2)dx 进行积分,结果得到1/3(n^3),微积分其实是考虑连续情况下的“求和”(但线性代数式离散的)。
![图片[6]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130117-6395d49d71c7f.jpg)
另一个问题:之前是 A 进行消元得到 U,那么加上右侧常数列 b,它需要多少次操作?把它放到消元步骤中,然后进行回代,一共需要 n square 次操作,要比 A 进行变换的次数少得多。因此,经常有矩阵 A 和几个右侧向量,这时对 A 进行更多次操作,将其分解乘 L 和 U,来完成消元,之后就可以以较少次数处理右侧向量了。这时方程组运算中最基本的运算问题。
Elimination on A requires about 1/3(n^3) multiplications and 1/3(n^3) subtractions.
2.3 solve Ax=b耗费次数
Each right side needs n^2 mutiplications and n^2 substractions.
即:
Factor change 1/3n^3 to n(w^2) Solve change (n^2) to 2nw.
三、转置与置换 permutations,置换矩阵群
若允许行互换,当主元位置为 0 时,要进行行互换,置换矩阵可以进行行互换。来看看 3 维下的所有置换矩阵:
![图片[7]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130117-6395d49deb6e5.jpg)
3 维下一共 3*2*1=6 个置换矩阵,他们形成的矩阵群有一些特点:
1)置换矩阵两两相乘结果仍然在该群中
2)取其逆,只用将行换回去,结果也在该群中
3)个别置换矩阵的逆矩阵就是其置换矩阵本身(比如上面的前 4 个,其转置等于本身),但对于所有的,
总结来说是:置换矩阵的逆是等于其转置。
——————————————————————————————————————————————————–
总结:1.LU分解
2.LU分解的运算复杂度
第五讲 转置-置换-向量空间R
在上节课中,我们讲述了求解矩阵逆的基本公式,同时讲解了A的LU分解。在这节课中我们将讲述矩阵的两种变换,分别是矩阵的置换、矩阵的转置和向量空间。核心思想是,通过某些向量构成一个向量组成的空间。这些向量属于R^n,构成的子空间也在R^n 中。
一、矩阵的置换(Permutation)
在维基百科中查到关于Permutation的定义,他的意思是将特定序列的元素重新排列。比如(1,2,3)这个序列的置换有(1,3,2)等。我们这里用3×3的单位矩阵做置换变换,看我们能得到哪些矩阵:
上面的六个矩阵分别是单位阵的六种置换变换(这里我们把他本身也算在内)。如果把矩阵理解为变换的话,那么他们分别表示将第一行与第二行进行互换的变换(图2)、第一行与第三行进行互换的变换(图3)、第一行变换到第二行,第二行变换到第三行,第三行变换到第一行的变换(图5)等等。
1.1 置换矩阵的注意点
在进行矩阵分解时A=LU,我们假设了没有行互换,现在我们取消这个假设,Matlab 会检查每个主元位置上是否为0,甚至对很小的接近于0 的数也进行行交换(因为这些数值运算上很难处理,会影响数值的准确性)。如何处理A=LU 中的行互换?对任意可逆矩阵,都有以下形式:
![图片[8]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130118-6395d49ee75a3.jpg)
二、矩阵的转置(Transpose)
矩阵的转置在没有讲之前我们已经接触过了,对于一个矩阵A有如下例子:
![图片[9]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130119-6395d49f8ad57.png)
那么他的转置为:
![图片[10]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130119-6395d49fcdc58.png)
很显然,一个矩阵的转置(A^T)_ji = A_ij。如果矩阵不为方阵,例如A是一个2×3的矩阵,那么转置后的矩阵为A^T为3×2。
我们把转置后等于自己本身的矩阵称之为对称矩阵(Symmetric),即存在A^T = A。可以看出对称矩阵一定是方阵,对称矩阵很特殊,但是也很常见。例如我们对一个矩阵R做如下计算即可获得对称矩阵:

矩阵R^(T)R = K,K是一个对称矩阵。
三、向量空间Vector spaces,子空间sub spaces
重点理解向量空间概念,子空间概念
3.1 向量空间
向量空间:表示有很多向量,一整个空间的向量。但并不是任意向量的组合都能成为空间。必须满足一定规则,必须能够进行加法和数乘运算,必须能够进行线性组合,对加法和数乘运算封闭。
把R^2 称为一个平面,X-Y 平面。可以将其考虑成所有向量的组合。
R^3 是所有三维实向量组成的向量空间。
R^n 包含所有的n 维向量,是n 维向量空间。
向量空间性质(或者说需要满足的规则):对加法和数乘运算封闭,或者说对线性组合封闭,即所有的空间内的向量线性组合后仍在空间内。
检验是否是空间(向量空间或者子空间)的方法就是看是否对那些运算封闭。
3.2 子空间
子空间:满足空间规则,但又不需包含所有向量。取某向量空间的部分空间(显然得到的就不是向量空间了),这部分中的向量不管是加法还是数乘,结果依然在此部分空间内,这就是子空间。
例:
R^2 的子空间:1)穿过原点的直线;2)原点;(特别注意,这不是零空间,只能说零向量是R2 的子空间)3)R^2
R^3 的子空间:1)穿过原点的直线;2)穿过原点的平面;3)原点;(特别注意,这不是零空间)4)R^3
3.3 矩阵的子空间的构造
通过列向量构造,R^3 中,矩阵A(举例只有2 列)这些列的所有线性组合构成一个子空间(得到一个平面,列共线的话就是一条直线),它也叫做列空间C(A),C 表示column 意思。
*******************************************************************************************************************
总结:
1. 置换矩阵; 2. 对称矩阵; 3. 向量空间和向量的子空间。
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
第六讲列空间和零空间
一、矩阵列空间
1.1 矩阵的列空间
矩阵A 的列空间C(A)是其列向量的所有线性组合所构成的空间。例如:
![图片[11]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130120-6395d4a0a316b.png)
矩阵A的所包含的列有(不包含如下0向量):
![图片[12]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130121-6395d4a10e786.png)
当矩阵的列及零向量自由组合即可形成一个子空间,这个子空间是经过原点的平面,他们是三维向量空间的子空间(矩阵的列向量为三维向量空间中的两个向量)
1.2 利用矩阵的列空间求解AX=b
求解Ax=b 的问题,对于给定的矩阵A,对于任意的b 都能得到解么?

矩阵A 列向量的线性组合无法充满
R4
,因此如果b不能被表示为A 列向量的线性组合时,方程是无解的。只有当b 在矩阵A 列空间C(A)里时,x 才有解。
而且,由于列向量不是线性无关的(第三个列向量为前两个列向量之和),所以尽管有3 个列向量,但是只有2 个对张成向量空间有贡献。矩阵A 的列空间为
R4
内的一个二维子空间。
二、矩阵的零空间(Null Space)
2.1 零空间的定义
矩阵A 的零空间N(A)是指满足Ax=0 的所有解的集合。x 为含有3 个分量的向量,故矩阵A 的零空间是
R3
的子空间。对于m*n 矩阵,列空间为
Rm
的子空间,零空间为
Rn
空间的子空间。对于Ax = 0:
![图片[13]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130121-6395d4a1a54c7.png)
其解空间也是三维的。我们能很容易看出他的解有(我们还没讲到对Ax=0的求解,但这个例子很简单就能看出):![图片[13]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130121-6395d4a1a54c7.png)
我们将解进一步表示为:
![图片[15]-MIT 线性代数(4—6)读书笔记-卡核](http://www.caxkernel.com/wp-content/uploads/2022/12/20221211130122-6395d4a20a770.png)
由这个解我们可以看出,它是三维空间中一条过原点的直线。则其解集不能构成列空间的一个子空间。因为:零向量并不在列空间的子空间这个集合内。
2.2 证明Ax=0是构成子空间
如果Av = 0 且 Aw = 0 那么A(v+w)= Av+Aw = 0;
同理,如果Av = 0 那么A(cv) = c(Av)= 0(c为常数)。
注:
1. Ax=b右侧b 向量取一个非0 向量,此时x 有解,(这时x 的解不是零空间了),那么所有的x 解构成子空间吗?很明显不构成子空间,或者说向量空间。因为很明显0 向量不在这个空间内,没有0 向量,就不用谈向量空间了(原因很明显,数乘运算中,常数取0 时需要满足封闭规则)。
2. 有两种方法构造子空间:1. 是通过列的线性组合构造列空间;2. 是求解向量必须满足的方程组来构造子空间(通过让x 满足特定条件来得到子空间,Ax=0 将构造出零空间)。
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
总结:
1. 列向量空间(Ax=b);2. 零向量空间(Ax=0);3. 这两个向量空间的维度。
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
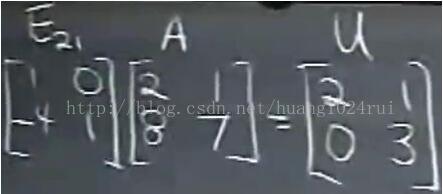








![[转]我国CAD软件产业亟待研究现状采取对策-卡核](https://www.caxkernel.com/wp-content/uploads/2024/07/frc-f080b20a9340c1a89c731029cb163f6a-212x300.png)








