第三十四讲：左右逆和伪逆

---

前面我们涉及到的逆（inverse）都是指左、右乘均成立的逆矩阵，即

A−1A=I=AA−1
A^{-1}A=I=AA^{-1}。在这种情况下，

m×n
m\\times n矩阵

A
A满足m=n=rank(A)m=n=rank(A)，也就是满秩方阵。

左逆（left inserve）

---

记得我们在最小二乘一讲（第十六讲）介绍过列满秩的情况，也就是列向量线性无关，但行向量通常不是线性无关的。常见的列满秩矩阵

A
A满足m=n=rank(A)m=n=rank(A)(

情况1
\\color{red}{情况1})。

列满秩时，列向量线性无关，所以其

零空间
\\color{red}{零空间}中只有零解，方程

Ax=b
Ax=b可能有一个唯一解（

b
b在AA的列空间中，此特解就是全部解，因为通常的特解可以通过零空间中的向量扩展出一组解集，而此时零空间只有列向量），也可能无解（

b
b不在AA的列空间中）。

另外，此时行空间为

Rn
\\mathbb{R}^n，也正印证了与行空间互为正交补的零空间中只有列向量。

现在来观察

ATA
A^TA，也就是在

m>n=rank(A)
m>n=rank(A)(

情况2
\\color{red}{情况2})的情况下，

n×m
n\\times m矩阵乘以

m×n
m\\times n矩阵，结果为一个满秩的

n×n
n\\times n矩阵，所以

ATA
A^TA是一个可逆矩阵。也就是说

(ATA)−1ATA=I
\\underbrace{\\left(A^TA\\right)^{-1}A^T}A=I成立，而大括号部分的

(ATA)−1AT
\\left(A^TA\\right)^{-1}A^T称为长方形矩阵

A
A的左逆

A^{-1}_{left}=\\left(A^TA\\right)^{-1}A^T

• 顺便复习一下最小二乘一讲，通过关键方程

  ATAx^=ATb
  A^TA\\hat x=A^Tb，

  A−1left
  A^{-1}_{left}被当做一个系数矩阵乘在

  b
  b向量上，求得bb向量投影在

  A
  A的列空间之后的解x^=(ATA)−1ATb\\hat
  x=\\left(A^TA\\right)^{-1}A^Tb。

• 如果我们强行给左逆左乘矩阵

  A
  A，得到的矩阵就是投影矩阵P=A(ATA)−1ATP=A\\left(A^TA\\right)^{-1}A^T，来自

  p=Ax^=A(ATA)−1AT
  p=A\\hat
  x=A\\left(A^TA\\right)^{-1}A^T，它将右乘的向量

  b
  b投影在矩阵AA的列空间中。

再来观察

AAT
AA^T矩阵，这是一个

m×m
m\\times m矩阵，秩为

rank(AAT)=n<m
rank(AA^T)=n<m，也就是说

AAT
AA^T是不可逆的，那么接下来我们看看右逆。

2.右逆（right inverse）

---

可以与左逆对称的看，右逆也就是研究

m×n
m\\times n矩阵

A
A行满秩的情况，此时n>m=rank(A)n>m=rank(A)。对称的，其

左零空间
\\color{red}{左零空间}中仅有零向量，即没有行向量的线性组合能够得到零向量。

行满秩时，矩阵的列空间将充满向量空间

C(A)=Rm
C(A)=\\mathbb{R}^m，所以方程

Ax=b
Ax=b总是有解集，由于消元后有

n−m
n-m个自由变量，所以方程的零空间为

n−m
n-m维。

与左逆对称，再来观察

AAT
AA^T，在

n>m=rank(A)
n>m=rank(A)(

情况3
\\color{red}{情况3})的情况下，

m×n
m\\times n矩阵乘以

n×m
n\\times m矩阵，结果为一个满秩的

m×m
m\\times m矩阵，所以此时

AAT
AA^T是一个满秩矩阵，也就是

AAT
AA^T可逆。所以

AAT(AAT)=I
A\\underbrace{A^T\\left(AA^T\\right)}=I，大括号部分的

AT(AAT)
A^T\\left(AA^T\\right)称为长方形矩阵的右逆

A^{-1}_{right}=A^T\\left(AA^T\\right)

同样的，如果我们强行给右逆右乘矩阵

A
A，将得到另一个投影矩阵P=AT(AAT)AP=A^T\\left(AA^T\\right)A，与上一个投影矩阵不同的是，这个矩阵的

A
A全部变为ATA^T了。所以这是一个能够将右乘的向量

b
b投影在AA的行空间中。

前面我们提及了逆（方阵满秩），并讨论了左逆（矩阵列满秩）、右逆（矩阵行满秩），现在看一下第四种情况，

m×n
m\\times n矩阵

A
A不满秩的情况。

3.伪逆（pseudo inverse）

3.1定义

---

有m×nm\\times n矩阵

A
A，满足rank(A)<min(m, n)rank(A)\\lt min(m,\\ n)(

情况4
\\color{red}{情况4})，则

• 列空间

  C(A)∈Rm, dimC(A)=r
  C(A)\\in\\mathbb{R}^m,\\ \\dim C(A)=r，左零空间

  N(AT)∈Rm, dimN(AT)=m−r
  N\\left(A^T\\right)\\in\\mathbb{R}^m,\\ \\dim N\\left(A^T\\right)=m-r，列空间与左零空间互为正交补；

• 行空间

  C(AT)∈Rn, dimC(AT)=r
  C\\left(A^T\\right)\\in\\mathbb{R}^n,\\ \\dim C\\left(A^T\\right)=r，零空间

  N(A)∈Rn, dimN(A)=n−r
  N(A)\\in\\mathbb{R}^n,\\ \\dim N(A)=n-r，行空间与零空间互为正交补。

现在任取一个向量

x
x，乘上AA后结果

Ax
Ax一定落在矩阵

A
A的列空间C(A)C(A)中。而根据维数，

x∈Rn, Ax∈Rm
x\\in\\mathbb{R}^n,\\ Ax\\in\\mathbb{R}^m，那么我们现在猜测，输入向量

x
x全部来自矩阵的行空间，而输出向量AxAx全部来自矩阵的列空间，并且是一一对应的关系，也就是

Rn
\\mathbb{R}^n的

r
r维子空间到Rm\\mathbb{R}^m的

r
r维子空间的映射。

而矩阵AA现在有这些零空间存在，其作用是将某些向量变为零向量，这样

Rn
\\mathbb{R}^n空间的所有向量都包含在行空间与零空间中，所有向量都能由行空间的分量和零空间的分量构成，变换将零空间的分量消除。但如果我们只看行空间中的向量，那就全部变换到列空间中了。

那么，我们现在只看行空间与列空间，在行空间中任取两个向量

x, y∈C(AT)
x,\\ y\\in C(A^T)，则有

Ax≠Ay
Ax\\neq Ay。所以从行空间到列空间，变换

A
A是个不错的映射，如果限制在这两个空间上，AA可以说“是个可逆矩阵”，那么它的逆就称作伪逆，而这个伪逆的作用就是将列空间的向量一一映射到行空间中。通常，伪逆记作

A+
A^+，因此

Ax=(Ax), y=A+(Ay)
Ax=(Ax),\\ y=A^+(Ay)。

现在我们来证明对于

x,y∈C(AT), x≠y
x,y\\in C\\left(A^T\\right),\\ x\\neq y，有

Ax,Ay∈C(A), Ax≠Ay
Ax,Ay\\in C(A),\\ Ax\\neq Ay：

• 反证法，设

  Ax=Ay
  Ax=Ay，则有

  A(x−y)=0
  A(x-y)=0，即向量

  x−y∈N(A)
  x-y\\in N(A)；

• 另一方面，向量

  x,y∈C(AT)
  x,y\\in C\\left(A^T\\right)，所以两者之差

  x−y
  x-y向量也在

  C(AT)
  C\\left(A^T\\right)中，即

  x−y∈C(AT)
  x-y\\in C\\left(A^T\\right)；

• 此时满足这两个结论要求的仅有一个向量，即零向量同时属于这两个正交的向量空间，从而得到

  x=y
  x=y，与题设中的条件矛盾，得证。

伪逆在统计学中非常有用，以前我们做最小二乘需要矩阵列满秩这一条件，只有矩阵列满秩才能保证

ATA
A^TA是可逆矩阵，而统计中经常出现重复测试，会导致列向量线性相关，在这种情况下

ATA
A^TA就成了奇异矩阵，这时候就需要伪逆。

3.2 伪逆求解

---

接下来我们介绍如何计算伪逆

A+
A^+：

• 其中一种方法是使用奇异值分解，

  A=UΣVT
  A=U\\varSigma V^T，其中的对角矩阵型为

  Σ=⎡⎣⎢⎢⎢⎢⎢⎢σ1⋱σ2[0]⎤⎦⎥⎥⎥⎥⎥⎥
  \\varSigma=\\left[\\begin{array}{c c c|c}\\sigma_1&&&\\\\&\\ddots&&\\\\&&\\sigma_2&\\\\\\hline&&&\\begin{bmatrix}0\\end{bmatrix}\\end{array}\\right]，对角线非零的部分来自

  ATA, AAT
  A^TA,\\ AA^T比较好的部分，剩下的来自左/零空间。

我们先来看一下

Σ
\\varSigma矩阵的伪逆是多少，这是一个

m×n
m\\times n矩阵，

rank(Σ)=r
rank(\\varSigma)=r，

Σ+=⎡⎣⎢⎢⎢⎢⎢⎢⎢1σ1⋱1σr[0]⎤⎦⎥⎥⎥⎥⎥⎥⎥
\\varSigma^+=\\left[\\begin{array}{c c c|c}\\frac{1}{\\sigma_1}&&&\\\\&\\ddots&&\\\\&&\\frac{1}{\\sigma_r}&\\\\\\hline&&&\\begin{bmatrix}0\\end{bmatrix}\\end{array}\\right]，伪逆与原矩阵有个小区别：这是一个

n×m
n\\times m矩阵。则有

ΣΣ+=⎡⎣⎢⎢⎢⎢⎢⎢1⋱1[0]⎤⎦⎥⎥⎥⎥⎥⎥m×m
\\varSigma\\varSigma^+=\\left[\\begin{array}{c c c|c}1&&&\\\\&\\ddots&&\\\\&&1&\\\\\\hline&&&\\begin{bmatrix}0\\end{bmatrix}\\end{array}\\right]_{m\\times m}，

Σ+Σ=⎡⎣⎢⎢⎢⎢⎢⎢1⋱1[0]⎤⎦⎥⎥⎥⎥⎥⎥n×n
\\varSigma^+\\varSigma=\\left[\\begin{array}{c c c|c}1&&&\\\\&\\ddots&&\\\\&&1&\\\\\\hline&&&\\begin{bmatrix}0\\end{bmatrix}\\end{array}\\right]_{n\\times n}。

观察

ΣΣ+
\\varSigma\\varSigma^+和

Σ+Σ
\\varSigma^+\\varSigma不难发现，

ΣΣ+
\\varSigma\\varSigma^+是将向量投影到列空间上的投影矩阵，而

Σ+Σ
\\varSigma^+\\varSigma是将向量投影到行空间上的投影矩阵。我们不论是左乘还是右乘伪逆，得到的不是单位矩阵，而是投影矩阵，该投影将向量带入比较好的空间（行空间和列空间，而不是左/零空间）。

• 接下来我们来求

  A
  A的伪逆：
  

  A+=VΣ+UT

  A^+=V\\varSigma^+U^T

4. 总结

---

1.

A是m×n
A是m×n，

m
m 行 nn 列
1）矩阵可逆：
即两边逆，

AA−1=I=A−1A
AA^{ -1} = I = A ^{-1} A ，此时

r=m=n
r=m=n，

A
A 为方阵且满秩，零空间和左零空间都只有零
向量。

2）左逆(m>n=rank(A)m>n=rank(A))：
当列满秩，列向量线性无关，行向量不一定，

r=n
r=n，零空间只有零向量，

Ax=b
Ax=b 存在 0 个或 1 个解。

ATA
A ^T A 是

n×n
n×n 的对称矩阵，满秩，

ATA
A ^T A 是可逆的，称

(ATA)−1AT
(A ^T A) ^{-1} A ^T 为

A
A 的左逆，因为(ATA)−1AT∗A=I(A T A)^{ -1} A ^T *A=I。这在最小二乘中至关重要，因为最小二乘以

ATA
A ^T A 为系数矩阵（为什么统计学家喜欢这些？因为统计学家最喜欢用最小二乘），在列满秩的情况下，

ATA
A ^T A 可逆。此时

[(ATA)−1AT]
[ (A ^T A) ^{-1} A ^T ]为

n×m
n×m，

A为m×n
A为m×n，得

I
I 为

n×n
n×n。

3）右逆(

n>m=rank(A)
n>m=rank(A))：
当行满秩，行向量线性无关，

r=m
r=m，

AT
A^ T 的零空间只含零向量，

Ax=b
Ax=b 有或无穷多个解，因为

A∗AT(AAT)−1=I
A*A^ T (AA ^T ) ^{-1} =I，所以把

AT(AAT)−1
A ^T (AA ^T ) ^{-1} 称为 A 的右逆。

4）伪逆(

rank(A)<min(m, n)
rank(A)\\lt min(m,\\ n))：

r<m,r<n
r<m,r<n，行空间和列空间的维数相同，都是

r
r 维，行空间的任意向量

x
x，与 AA 相乘，得到恰好是列空间中的所有向量，行空间向量

x
x 与列空间向量

Ax
Ax 的关系是一 一对应的。所有向量都能由行空间的分量和零空间的分量构成。

• 行空间中向量

  x
  x 对应着列空间中的 AxAx（零空间中的

  x
  x 乘以

  A
  A 得零 Ax=0Ax=0）， 行空间中向量

  y
  y 对应着列空间中的 AyAy。

• 但如果要从列空间得到行空间的向量呢，要得到行空间的向量，那么

  x=A+(Ax)
  x=A ^+ (Ax)，

  A+
  A ^+ 就是伪逆，伪逆把左零空间变为

  0
  0，即如果 A+A^+ 乘以左零空间的向量，结果为

  0
  0。

• 假设没有零空间的干扰，即假设零空间只有零向量，存在逆，那么行空间的向量x x 得到列空间的向量

  Ax
  Ax，反过来，通过

  A
  A 的逆就能从列空间得到行空间， A−1(Ax)=xA ^{-1} (Ax)=x。

• (ATA)−1AT∗A=I
  (A ^T A) ^{-1} A^ T *A=I， 如果将左逆写在右边将得不到单位矩阵了， 那么

  A(ATA)−1AT
  A(A ^T A) ^{-1} A ^T 是在列空间投影的投影矩阵，它会尽量靠近单位矩阵，一个投影矩阵很想成为单位矩阵，但不可能做到。

2.求解伪逆（SVD分解）

第三十五讲：期末复习

依然是从以往的试题入手复习知识点。

1.
已知

m×n
m\\times n矩阵

A
A，有Ax=⎡⎣⎢100⎤⎦⎥Ax=\\begin{bmatrix}1\\\\0\\\\0\\end{bmatrix}无解；

Ax=⎡⎣⎢010⎤⎦⎥
Ax=\\begin{bmatrix}0\\\\1\\\\0\\end{bmatrix}仅有唯一解，求关于

m,n,rank(A)
m,n,rank(A)的信息。

首先，最容易判断的是

m=3
m=3；而根据第一个条件可知，矩阵不满秩，有

r<m
r<m；根据第二个条件可知，零空间仅有零向量，也就是矩阵消元后没有自由变量，列向量线性无关，所以有

r=n
r=n。

综上，有

m=3>n=r
m=3>n=r。

根据所求写出一个矩阵

A
A的特例：A=⎡⎣⎢010001⎤⎦⎥A=\\begin{bmatrix}0& 0\\\\1& 0\\\\0& 1\\end{bmatrix}。

detATA=?detAAT
\\det A^TA\\stackrel{?}{=}\\det AA^T：不相等，因为

ATA
A^TA可逆而

AAT
AA^T不可逆，所以行列式不相等。（但是对于方阵，

detAB=detBA
\\det AB=\\det BA恒成立。）

• ATA
  A^TA可逆吗？是，因为

  r=n
  r=n，矩阵列向量线性无关，即列满秩。

• AAT
  AA^T正定吗？否，因为

  AAT
  AA^T是

  3×n
  3\\times n矩阵与

  n×3
  n\\times 3矩阵之积，是一个三阶方阵，而

  AAT
  AA^T秩为

  2
  2，所以不是正定矩阵。（不过AATAA^T一定是半正定矩阵。）

  求证

  ATy=c
  A^Ty=c至少有一个解：因为

  A
  A的列向量线性无关，所以ATA^T的行向量线性无关，消元后每行都有主元，且总有自由变量，所以零空间中有非零向量，零空间维数是

  m−r
  m-r（可以直接从

  dimN(AT)=m−r
  \\dim N\\left(A^T\\right)=m-r得到结论）。

---

2.
设

A=[v1 v2 v3]
A=\\Bigg[v_1\\ v_2\\ v_3\\Bigg]，对于

Ax=v1−v2+v3
Ax=v_1-v_2+v_3，求

x
x。

按列计算矩阵相乘，有x=⎡⎣⎢1−11⎤⎦⎥x=\\begin{bmatrix}1\\\\-1\\\\1\\end{bmatrix}。

• 若

  Ax=v1−v2+v3=0
  Ax=v_1-v_2+v_3=0，则解是唯一的吗？为什么。如果解释唯一的，则零空间中只有零向量，而在此例中

  x=⎡⎣⎢1−11⎤⎦⎥
  x=\\begin{bmatrix}1\\\\-1\\\\1\\end{bmatrix}就在零空间中，所以解不唯一。

• 若

  v1,v2,v3
  v_1,v_2,v_3是标准正交向量，那么怎样的线性组合

  c1v1+c2v2
  c_1v_1+c_2v_2能够最接近

  v3
  v_3？此问是考察投影概念，由于是正交向量，所以只有

  0
  0向量最接近v3v_3。

---

3.
矩阵

A=⎡⎣⎢.2.4.4.4.2.4.3.3.4⎤⎦⎥
A=\\begin{bmatrix}.2& .4& .3\\\\.4& .2& .3\\\\.4& .4& .4\\end{bmatrix}，求稳态。

这是个马尔科夫矩阵，前两之和为第三列的两倍，奇异矩阵总有一个特征值为

0
0，而马尔科夫矩阵总有一个特征值为11，剩下一个特征值从矩阵的迹得知为

−.2
-.2。

再看马尔科夫过程，设从

u(0)
u(0)开始，

uk=Aku0,u0=⎡⎣⎢0100⎤⎦⎥
u_k=A^ku_0, u_0=\\begin{bmatrix}0\\\\10\\\\0\\end{bmatrix}。先代入特征值

λ1=0, λ2=1, λ3=−.2
\\lambda_1=0,\\ \\lambda_2=1,\\ \\lambda_3=-.2查看稳态

uk=c1λk1x1+c2λk2x2+c3λk3x3
u_k=c_1\\lambda_1^kx_1+c_2\\lambda_2^kx_2+c_3\\lambda_3^kx_3，当

k→∞
k\\to\\infty，第一项与第三项都会消失，剩下

u∞=c2x2
u_\\infty=c_2x_2。

到这里我们只需求出

λ2
\\lambda_2对应的特征向量即可，带入特征值求解

(A−I)x=0
(A-I)x=0，有

⎡⎣⎢−.8.4.4.4−.8.4.3.3−.6⎤⎦⎥⎡⎣⎢???⎤⎦⎥=⎡⎣⎢000⎤⎦⎥
\\begin{bmatrix}-.8& .4& .3\\\\.4& -.8& .3\\\\.4& .4& -.6\\end{bmatrix}\\begin{bmatrix}?\\\\?\\\\?\\end{bmatrix}=\\begin{bmatrix}0\\\\0\\\\0\\end{bmatrix}，可以消元得，也可以直接观察得到

x2=⎡⎣⎢334⎤⎦⎥
x_2=\\begin{bmatrix}3\\\\3\\\\4\\end{bmatrix}。

剩下就是求

c2
c_2了，可以通过

u0
u_0一一解出每个系数，但是这就需要解出每一个特征值。另一种方法，我们可以通过马尔科夫矩阵的特性知道，对于马尔科夫过程的每一个

uk
u_k都有其分量之和与初始值分量之和相等，所以对于

x2=⎡⎣⎢334⎤⎦⎥
x_2=\\begin{bmatrix}3\\\\3\\\\4\\end{bmatrix}，有

c2=1
c_2=1。所以最终结果是

u∞=⎡⎣⎢334⎤⎦⎥
u_\\infty=\\begin{bmatrix}3\\\\3\\\\4\\end{bmatrix}。

---

4.
对于二阶方阵，回答以下问题：

求投影在直线

a=[4−3]
a=\\begin{bmatrix}4\\\\-3\\end{bmatrix}上的投影矩阵：应为

P=aaTaTa
P=\\frac{aa^T}{a^Ta}。

已知特征值

λ1=2, x1=[12]λ2=3, x2=[21]
\\lambda_1=2,\\ x_1=\\begin{bmatrix}1\\\\2\\end{bmatrix}\\quad \\lambda_2=3,\\ x_2=\\begin{bmatrix}2\\\\1\\end{bmatrix}求原矩阵

A
A：从对角化公式得A=SΛS−1=[1221][0003][1221]−1A=S\\Lambda S^{-1}=\\begin{bmatrix}1& 2\\\\2& 1\\end{bmatrix}\\begin{bmatrix}0& 0\\\\0& 3\\end{bmatrix}\\begin{bmatrix}1& 2\\\\2& 1\\end{bmatrix}^{-1}，解之即可。

A
A是一个实矩阵，且对任意矩阵BB，

A
A都不能分解成A=BTBA=B^TB，给出

A
A的一个例子：我们知道BTBB^TB是对称的，所以给出一个非对称矩阵即可。 矩阵

A
A有正交的特征向量，但不是对称的，给出一个AA的例子：我们在三十三讲提到过，反对称矩阵，因为满足

AAT=ATA
AA^T=A^TA而同样具有正交的特征向量，所以有

A=[0−110]
A=\\begin{bmatrix}0& 1\\\\-1& 0\\end{bmatrix}或旋转矩阵

[cosθsinθ−sinθcosθ]
\\begin{bmatrix}\\cos\\theta& -\\sin\\theta\\\\\\sin\\theta& \\cos\\theta\\end{bmatrix}，这些矩阵都具有复数域上的正交特征向量组。

---

5.最小二乘问题，因为时间的关系直接写出计算式和答案，

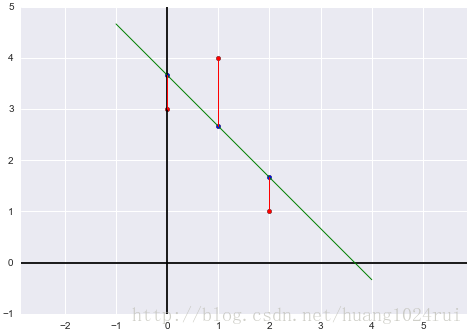
⎡⎣⎢111012⎤⎦⎥[CD]=⎡⎣⎢341⎤⎦⎥(Ax=b)
\\begin{bmatrix}1& 0\\\\1& 1\\\\1& 2\\end{bmatrix}\\begin{bmatrix}C\\\\D\\end{bmatrix}=\\begin{bmatrix}3\\\\4\\\\1\\end{bmatrix}(Ax=b)，解得

[C^D^]=[113−1]
\\begin{bmatrix}\\hat C\\\\\\hat D\\end{bmatrix}=\\begin{bmatrix}\\frac{11}{3}\\\\-1\\end{bmatrix}。

求投影后的向量

p
p：向量pp就是向量

b
b在矩阵AA列空间中的投影，所以

p=⎡⎣⎢p1p2p3⎤⎦⎥=⎡⎣⎢111012⎤⎦⎥[C^D^]
p=\\begin{bmatrix}p_1\\\\p_2\\\\p_3\\end{bmatrix}=\\begin{bmatrix}1& 0\\\\1& 1\\\\1& 2\\end{bmatrix}\\begin{bmatrix}\\hat C\\\\\\hat D\\end{bmatrix}。

求拟合直线的图像：

x=0,1,2
x=0,1,2时

y=p1,p2,p2
y=p_1,p_2,p_2所在的直线的图像，

y=C^+D^x
y=\\hat C+\\hat Dx即

y=113−x
y=\\frac{11}{3}-x。

• 接上面的题目

  求一个向量

  b
  b使得最小二乘求得的[C^D^]=[00]\\begin{bmatrix}\\hat C\\\\\\hat D\\end{bmatrix}=\\begin{bmatrix}0\\\\0\\end{bmatrix}：我们知道最小二乘求出的向量

  [C^D^]
  \\begin{bmatrix}\\hat C\\\\\\hat D\\end{bmatrix}使得

  A
  A列向量的线性组合最接近bb向量（即

  b
  b在AA列空间中的投影），如果这个线性组合为

  0
  0向量（即投影为00），则

  b
  b向量与AA的列空间正交，所以可以取

  b=⎡⎣⎢1−21⎤⎦⎥
  b=\\begin{bmatrix}1\\\\-2\\\\1\\end{bmatrix}同时正交于

  A
  <script type="math/tex" id="MathJax-Element-275">A</script>的两个列向量。