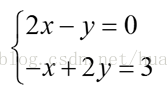MIT线性代数的总整理

第一讲：方程组的几何解释

    1.对一个方程组行形式，列形式。

    2.矩阵与向量相乘的方法（左行右列）

第二讲：矩阵消元

   1.消元法（成功、失败）

   2.消元矩阵（左行右列的真正意义）

第三讲 矩阵的乘法和逆矩阵（非奇异矩阵）

     1.矩阵乘法（5种形式）

     2.矩阵的逆（判定（3种形式），求解逆矩阵）

第四讲 矩阵A的LU分解

     1. A=LU 和A=LDU分解

    2. Ax=b的运算复杂度 

第五讲  转置-置换-向量空间R

     1. 矩阵的置换（3个注意点）

     2. 矩阵的转置（我们把转置后等于自己本身的矩阵称之为对称矩阵）

     3. 向量空间和子空间（向量空间（能够进行加法和数乘运算，必须能够进行线性组合，对加法和数乘运算封闭。），子空间（属于母空间，但自身又构成向量空间））

第六讲 列空间和零空间

      1. 列向量空间（Ax=b，此时空间的维度）

      2.零向量空间（Ax=0，此时空间的维度）

第七讲 求解Ax=0主变量特解

 第十讲 四个基本子空间

 
   1. 矩阵空间与微分方程

     2.秩1矩阵与其组成的向量空间

     3.小世界图

第十二讲 图与网络（应用）

• 将电势记为e，则在引入电势的第一步中，有e=Ax；
• 电势差导致电流产生，y=Ce；(电流y 等于电势差的常数倍，欧姆定律）
• 电流满足基尔霍夫定律方程，(A^T)y=0；(基尔霍夫电流定律，在没有外部电源电压的影响下f设为0）

上述三式是在无电源情况下的方程。

1.电源可以通过：在边上加电池（电压源），或在节点上加外部电流 两种方式接入。

2.如果在边上加电池，会体现在e=Ax中；如果在节点上加电流，会体现在(A^T)y=f中，f向量就是外部电流。

3.将以上三个等式连起来得到(A^T)CAx=f。另外，最后一个方程是一个平衡方程，还需要注意的是，方程仅描述平衡状态，方程并不考虑时间。最后，(A^T)A是一个对称矩阵。

第十三讲 总结1

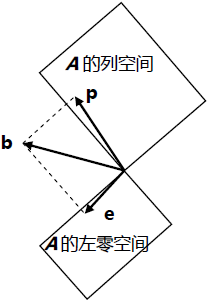
第十四讲 正交空间与子空间（Ax=b）

第十五讲 子空间的投影和Ax=b

1.投影矩阵及其应用；

2.解决Ax=b无解时，最优解的问题；

3.最小二乘法。

第十六讲投影矩阵(Ax=b)和最小二乘法

1.记住图：

2.最小二乘法求解的意义。 
3.

ATA
可逆的条件和正交向量组。

第十七讲正交矩阵和Gram-Schmidt正交化

1.标准正交基与正交矩阵； 
2.Gram-Schmidt正交标准化； 
3.QR分解（与LU分解的区别）。

第十八讲 行列式的性质

1.三大基本性质

2.7大推导的性质

第十九讲 行列式公式和代数余子式

1.行列式展开的正负号； 
2.计算行列式的三种方法； 
3.代数余子式求解时的正负号。

第二十讲 克拉默法则、逆矩阵、体积

1. 利用克拉默法则求矩阵的逆；

A−1=1detACT

第二十一讲 特征值和特征向量

1.特征向量和特征值的由来； 
2.3个例子得出的结论（对称矩阵、旋转矩阵、三角矩阵的特征值与特征向量的特点）。

第二十二讲 对角化和A的幂

第二十三讲 微分方程和

eAt

第二十四讲 马尔可夫矩阵、傅立叶级数

第二十五讲 复习2

第二十六讲 对称矩阵及正定矩阵

第二十七讲  复数矩阵和快速傅里叶变换

第二十八讲 正定矩阵和最小值

第二十九讲 相似矩阵和若尔当行形

第三十讲 奇异值分解

第三十一讲 线性变换及对应矩阵

第三十二讲 基变换与压缩感知

1. 图像压缩（定义，小波，傅立叶）；
2. 基变换

第三十三讲 单元测试与总结

第三十四将 左右逆和伪逆

第三十五讲 总结

线性代数学习完毕。