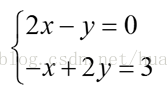第十讲：四个基本子空间

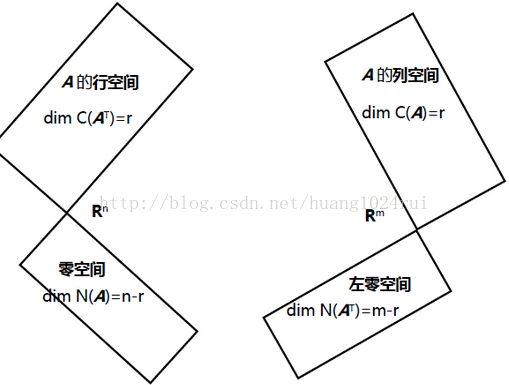
假设A是m×n，列空间C(A)，零空间N(A)，行空间C(A^T)，A转置的零空间(通常叫左零空间)N(A^T)，这是线性代数的核心内容，研究这四个基本子空间及其关系。我们从上一讲中的基、维数对这四个空间进行学习。

1.维数

1.1四种空间的定义

A是m*n的矩阵。

零空间N(A)：n 维向量，是Ax=0 的解，所以N(A)在R^n里。

列空间C(A): 列向量是m维的，所以C(A)在R^m里。

行空间C(A^T):A的行的所有线性组合，即A转置的列的线性组合（因为我们不习惯处理行向量C(A^T)在R^n里。

A的左零空间N(A^T)：A转置的零空间N(A^T)在R^m里面。

1.2 四种空间的维数

四种空间的维数是多少dimension？

列空间C(A)：A的主列就是列空间的一组基，dim(C(A))=Rank(A)=r，维数就是秩的大小。

行空间C(A^T)：dim(C(A^T))=Rank(A)=r，有一个重要的性质：行空间和列空间维数相同，都等于秩的大小。

零空间N(A)：一组基就是一组特殊解，r 是主变量的个数，n-r 是自由变量的个数，零空间的维数等于n-r,即dim(N(A))=n-r。

左零空间N(A^T)：矩阵A^T有m 列,而其秩为r，因此A^T自由列数目为m-r,所以dim(N(A^T))=m-r。

行空间和零空间在R^n 里，他们的维数加起来等于n，列空间和左零空间在R^m里，他们的维数加起来等于m。如下图所示：

图片[1]-MIT 线性代数（10—12）读书笔记-卡核

1.3对这四个空间进行总结

1）n维空间中存在两个子空间，一个r维的行空间，一个n-r维的零空间，维数和为n。和另一个结论相似（在求解Ax=b处）：
r 个主变量，n-r 个是自由变量，加起来是n。
2）m维空间中存在两个子空间，一个r维的列空间，一个m-r维的左零空间，维数和为m。

2.基

列空间C(A)：主列组合就是一组基。

零空间N(A)：Ax=0一组特殊解就是一组基。

行空间C(A^T)：通过初等行变换变换成行最简式，行空间的一组基即是行最简形R 的前r(秩数)行。（行变换不会对行空间产生影响，但会对列空间产生影响。）

例如：

图片[2]-MIT 线性代数（10—12）读书笔记-卡核

A通过初等行变换得到R，前两行就是行空间的一组基，为什么说它们一定在矩阵的行空间里？
因为行变换的时候是某行和令一行相加或相减，即是这些行向量的的线性组合。

左零空间N(A^T)：为什么叫左零空间？
A^T*y=0，将等式左右两边都转置，得：y^T*A=0^T，如下，所以叫左零空间。图片[3]-MIT 线性代数（10—12）读书笔记-卡核

但我们一般还是习惯用ATy=0，因为希望y 是列向量。
求矩阵的左零空间，就试着寻找一个产生零行向量的行组合，求矩阵的零空间，就试着寻找一个产生零列向量的列组合。

图片[4]-MIT 线性代数（10—12）读书笔记-卡核

如上，求A得左零空间，通过行变换得到R，R的最后一行是0 向量，行变换的逆变换E 的最后一行即是A的各行的组合产生0 向量的向量。即，左零空间的一组基为[-1,0,1]

3.总结

1）四种空间的定义和维度。

2）四种空间的基向量（由哪些向量张成的空间）。

——————————————————————————————————————————————————

第十一讲矩阵空间、秩1空间和小世界图

本章节分三部分：把矩阵空间的定义从向量的形式扩展到矩阵和微分方程的的形式；任何举证都能由秩1矩阵导出；利用矩阵的相关知识可以导出图中的知识，引出下一章的知识。

1.矩阵空间

1.1 引子

所有的3*3 矩阵，把矩阵看着"向量"，每个3*3 的矩阵都是一个"向量"，叫他们为向量，因为他们服从向量加法，乘法，又能够对矩阵进行线性组合。向量空间，关心的是A+B 和cA。子空间比如上三角矩阵，对称矩阵，子空间的交集也是子空间。关注他们的维数，基。3*3 的对角矩阵的维数为3，一组基为

认为这三个矩阵相互线性无关，而且任何的对角矩阵可通过这三个组合得到，因此他们生成了对角矩阵空间。我们把R^n 的概念延伸至R^(n*n)，他们仍对加法和乘法封闭。

1.2矩阵空间的定义

矩阵空间，可看作是新的向量空间，比如3×3的矩阵，它们加法或数乘都停留在3×3矩阵空间，3×3矩阵有一些子空间：1）3×3对称矩阵的子空间（两个对称矩阵相加还是对称的，数乘对称矩阵还是对称的），2）3×3的上三角矩阵的子空间等。考查它们的基，维数。

M：3×3 的所有矩阵，它的维数是9，一组基是：

我们所处的空间与这9维空间几乎相同，只是9个基是写为一个方阵而不是一列。

此矩阵空间的子空间和它的基与维数是：

1）S：3×3 的对称矩阵
S维数是6，一组基是：对角线三个元素和对角线以上的3个元素分别为1 其余为0的6个矩阵（由这6个矩阵就可得到所有的3×3 的对称矩阵了，因为下三角的元素可由上三角的元素可知结果）。

2）U：3×3 的上三角矩阵

U维数是6，一组基是：上三角的6个元素分别为1其余为0。

3）S∩U 对称矩阵交上三角矩阵维数是3（就只有对角线上有非0元素）。

4）S+U（注意不是S∪U，因为它不构成子空间）取S内任一元素(矩阵)加上U内任一元素(矩阵)即可，它可以得到所有3×3矩阵，而很明显它的维数是9，而不是dim(S)+dim(U)=dim(S∩U)+dim(S+U)=6+6=3+9。

1.3微分方程的解空间

微分方程的解空间（要点在于有些东西不像向量，但我们可以称它们为向量，可以做加法，数乘，线性组合，这就是为什么线性代数、基、维度等概念不仅仅用于我们一直讨论的m×n矩阵）。例如：

通过1.1到1.3可以看到，空间的定义可以扩展到矩阵、微分方程等带有参数的解的形式。

2.秩1矩阵

2.1定义

所有秩1 的矩阵都可表示为一列乘以一行的形式：A=U(V^T)，U是列向量，V也是列向量。例如：

我们在抽象的想：秩1矩阵可以就像搭建其他矩阵的积木一样，如果有5×17 的矩阵，秩为4，可以把这5×17 的矩阵分解为4个秩1矩阵的组合。

问题：秩1 矩阵组成的集合是子空间吗？

假设矩阵空间M的所有5×17的矩阵，一个由秩4矩阵组成的子集，子集中两个矩阵相加结果很可能是一个秩为5矩阵，而不是秩4矩阵。由秩1 矩阵组成的子集，相加结果很可能是一个秩2 矩阵。这说明，它的秩1矩阵组成的子集不是子空间。

2.2 秩1矩阵所组成的向量空间

假设R^4中，假设各分量之和为零的所有向量构成的集合S，即：

S能否构成一个子空间？

能，因为这些向量数乘常数或相加后仍等于0，那么子空间S的基和维数是怎样的？

3.小世界图

运用小世界引出图论和线性代数的关系。

图是结点和边的集合，边连通各个结点。比如一个5 个点6 条边的图可以用一个5×6 的矩阵完全表示。一个有趣的问题是：一个由很多结点和很多条边组成的图，最大的两点距离是多少？有研究表明，通常不超过6步。这就是小世界的来源，下一讲会细讲。

———————————————————————————————————————————————————————————————————-

第十二讲图和网络

本讲着重于线性代数的应用，线性代数处理的矩阵都是有出处的，来自实际问题，描述问题的拓扑结构。应用数学中最重要的模型，离散数学称之为”图“。我们从图和矩阵推导出欧姆定律、基尔霍夫电流定律、欧拉公式之间的关系。(此章节中x可认为是电势、y认为是电流)

1.图和矩阵与欧姆定律、基尔霍夫电流定理

1.1提出问题

假设一个电路图，4个结点，n=4，5条边，m=5，用矩阵来表示这些信息，这个矩阵叫做关联矩阵(Incidence Matrix)。其中：用矩阵A来表示，正负表示方向，每一行表示一条边。

将1,2,3 条边表示出来后，这三条边是一个回路，从这个子图的矩阵中，这三行是线性相关的，行1+行2=行3，说明”回路“意味着”相关“，与回路对应的行是线性相关的。

关联矩阵源于问题，描述了问题的拓扑结构，它可能是一个非常稀疏的矩阵。

1.2引出欧姆定律和基尔霍夫电流定理

矩阵A的零空间是什么（回顾：零空间告诉我们，如何对列向量进行组合可得到零向量，如果存在非0组合则说明列向量线性相关，如果只存在0组合得到零向量，则说明列向量线性无关）。

我们现在看矩阵A转置的零空间（即(A^T)y=0）。

假设矩阵C把电势差和电流联系起来，它的元素表示各边上的电流值y_1,y_2,y_3,y_4,y_5，电流和电势差的关系服从欧姆定律（欧姆定律：边上的电流值是电势差的倍数，这个倍数就是边的电导（conductance）即电阻（resistance）的倒数，告诉我们产生了多少电流）。

而(A^T)y=0的另一个名字叫做“基尔霍夫电流定律”（Kirchoff's Law, 简称KCL）。

2.图和矩阵与欧拉公式

2.1 (A^T)y=0的解

2.2 引出欧拉公式

A的行空间是怎样的？即求(A^T)的列空间。

列1，列2，列4 是主列，在电路图中看，那三条边是没有回路的，线性无关等价于没有回路。

由4个节点与3条边组成的图没有回路，就表明(A^T)的对应列向量线性无关，也就是节点数减一（rank=node-1）条边线性无关。另外，没有回路的图也叫作树（Tree）。

dim(N(A^T))=m-r，即
线性无关(两回路之间无关)的回路数量#loops=边的数量#edges-列空间的秩#rank（等于n-1，结点的数量-1，1 为A 零空间的维）
#loops = #edges – (#nodes-1)
#nodes – #edges + #loops = 1
这对任何图都成立，这就是欧拉公式（用线性代数证明欧拉公式）。