第十九讲 行列式公式和代数余子式

---

1.行列式公式

上一讲中，我们从三个简单的性质扩展出了一些很好的推论，本讲将继续使用这三条基本性质：

1. detI=1
   \\det I=1；

2. 交换行行列式变号；
3. 对行列式的每一行都可以单独使用线性运算，其值不变。

我们使用这三条性质推导二阶方阵行列式：

\\begin{vmatrix}a& b\\\\c& d\\end{vmatrix}=\\begin{vmatrix}a& 0\\\\c& d\\end{vmatrix}+\\begin{vmatrix}0& b\\\\c& d\\end{vmatrix}=\\begin{vmatrix}a& 0\\\\c& 0\\end{vmatrix}+\\begin{vmatrix}a& 0\\\\0& d\\end{vmatrix}+\\begin{vmatrix}0& b\\\\c& 0\\end{vmatrix}+\\begin{vmatrix}0& b\\\\0& d\\end{vmatrix}=ad-bc

按照这个方法，我们继续计算三阶方阵的行列式，可以想到，我们保持第二、三行不变，将第一行拆分为个行列式之和，再将每一部分的第二行拆分为三部分，这样就得到九个行列式，再接着拆分这九个行列式的第三行，最终得到二十七个行列式。可以想象到，这些矩阵中有很多值为零的行列式，我们只需要找到不为零的行列式，求和即可。

\\begin{vmatrix}a_{11}& a_{12}& a_{13}\\\\a_{21}& a_{22}& a_{23}\\\\a_{31}& a_{32}& a_{33}\\end{vmatrix}=\\begin{vmatrix}a_{11}& 0& 0\\\\0& a_{22}& 0\\\\0& 0& a_{33}\\end{vmatrix}+\\begin{vmatrix}a_{11}& 0& 0\\\\0& 0& a_{23}\\\\0& a_{32}& 0\\end{vmatrix}+\\begin{vmatrix}0& a_{12}& 0\\\\a_{21}& 0& 0\\\\0& 0& a_{33}\\end{vmatrix}+\\begin{vmatrix}0& a_{12}& 0\\\\0& 0& a_{23}\\\\a_{31}& 0& 0\\end{vmatrix}
+\\begin{vmatrix}0& 0& a_{13}\\\\a_{21}& 0& 0\\\\0& a_{32}& 0\\end{vmatrix}+\\begin{vmatrix}0& 0& a_{13}\\\\0& a_{22}& 0\\\\a_{31}& 0& 0\\end{vmatrix}

原式=a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31} \\tag{1}

同理，我们想继续推导出阶数更高的式子，按照上面的式子可知

n
n阶行列式应该可以分解成n!n!个非零行列式（占据第一行的元素有

n
n种选择，占据第二行的元素有n−1n-1种选择，以此类推得

n!
n!）：

\\det A=\\sum_{n!} \\pm a_{1\\alpha}a_{2\\beta}a_{3\\gamma}\\cdots a_{n\\omega}, (\\alpha, \\beta, \\gamma, \\omega)=P_n^n\\tag{2}

这个公式还不完全，接下来需要考虑如何确定符号：

\\begin{vmatrix}0& 0& \\overline 1& \\underline 1\\\\0& \\overline 1& \\underline 1& 0\\\\\\overline 1& \\underline 1& 0& 0\\\\\\underline 1& 0& 0& \\overline 1\\end{vmatrix}

如上图矩阵所示：

• 观察带有下划线的元素，它们的排列是

  (4,3,2,1)
  (4,3,2,1)，变为

  (1,2,3,4)
  (1,2,3,4)需要两步操作，所以应取

  +
  +正；

• 观察带有上划线的元素，它们的排列是(3,2,1,4)(3,2,1,4)，变为

  (1,2,3,4)
  (1,2,3,4)需要一步操作，所以应取

  −
  -负。

• 观察其他元素，我们无法找出除了上面两种以外的排列方式，于是该行列式值为零，这是一个奇异矩阵。

即正负号的选取\\color{red}{正负号的选取}可以是：用逆序数判断，即我们把全排列的顺序写出来，比如第一行我们选了第2列，第二行选第3列，第三行选第1列，那么序列就是231，逆序数就是从左到右遍历每一个数，统计右侧有几个数比自己小，这里231，2之后有一个，3之后也有一个，共二个，称此为偶排列，奇数次则为奇排列。偶排列时取正号，奇排列取负，原理在于对一个排列做一次交换后奇排列变偶排列，偶排列变奇排列，而123456…n是偶排列，必须为加。

2.代数余子式 cofactors

---

此处引入代数余子式（cofactor）的概念，它的作用是把

n
n阶行列式化简为n−1n-1阶行列式。

于是我们把

(1)
(1)式改写为：

a_{11}(a_{22}a_{33}-a_{23}a_{32})+a_{12}(a_{21}a_{33}-a_{23}a_{31})+a_{13}(a_{21}a_{32}-a_{22}a_{31})

\\begin{vmatrix}a_{11}& 0& 0\\\\0& a_{22}& a_{23}\\\\0& a_{32}& a_{33}\\end{vmatrix}+\\begin{vmatrix}0& a_{12}& 0\\\\a_{21}& 0& a_{23}\\\\a_{31}& 0& a_{33}\\end{vmatrix}+\\begin{vmatrix}0& 0& a_{13}\\\\a_{21}& a_{22}& 0\\\\a_{31}& a_{32}& 0\\end{vmatrix}

于是，我们可以定义

aij
a_{ij}的代数余子式：将原行列式的第

i
i行与第jj列抹去后得到的

n−1
n-1阶行列式记为

Cij
C_{ij}，

i+j为偶时时取+，i+j为奇时取−
\\color{red}{i+j为偶时时取+，i+j为奇时取-}。

现在再来完善式子

(2)
(2)：将行列式

A
A沿第一行展开：

\\det A=a_{11}C_{11}+a_{12}C_{12}+\\cdots+a_{1n}C_{1n}

到现在为止，我们了解了

三种求行列式的方法
\\color{red}{三种求行列式的方法}：

1. 消元，detA就是主元的乘积
   \\color{red}{消元，\\det A就是主元的乘积}；

2. 使用(2)式展开，求n!项之积
   \\color{red}{使用(2)式展开，求n!项之积}；

3. 使用代数余子式
   \\color{red}{使用代数余子式}。

对于矩阵行列式的计算，消元的得到主元是一个很好的方法，与之相比行列式的展开公式较为复杂，而代数余子式的方法介于两者之间，它的核心想法是通过降阶来将原来的行列式展开成更简单的行列式。

计算例题：

A4=∣∣∣∣∣∣1100111001110011∣∣∣∣∣∣=沿第一行展开∣∣∣∣110111011∣∣∣∣−∣∣∣∣100111011∣∣∣∣=−1−0=−1
A_4=\\begin{vmatrix}1& 1& 0& 0\\\\1& 1& 1& 0\\\\0& 1& 1& 1\\\\0& 0& 1& 1\\end{vmatrix}\\stackrel{沿第一行展开}{=}\\begin{vmatrix}1& 1& 0\\\\1& 1& 1\\\\0& 1& 1\\end{vmatrix}-\\begin{vmatrix}1& 1& 0\\\\0& 1& 1\\\\0& 1& 1\\end{vmatrix}=-1-0=-1

可观察出周期为6：

3.总结

---

1.行列式展开的正负号；
2.计算行列式的三种方法；
3.代数余子式求解时的正负号。

---

第二十讲：克拉默法则、逆矩阵、体积

本讲主要介绍逆矩阵的应用。

1.求逆矩阵

我们从逆矩阵开始，对于二阶矩阵有

[acbd]−1=1ad−bc[d−c−ba]
\\begin{bmatrix}a& b\\\\c& d\\end{bmatrix}^{-1}=\\frac{1}{ad-bc}\\begin{bmatrix}d& -b\\\\-c& a\\end{bmatrix}。观察易得，系数项就是行列式的倒数，而矩阵则是由一系列代数余子式组成的。先给出公式：

A−1=1detACT(1)

A^{-1}=\\frac{1}{\\det A}C^T \\tag{1}


注:

1. 矩阵外因子的分母是矩阵的行列式的值，而矩阵是“代数余子式矩阵”（cofactor matrix）C的转置，常被称为”

伴随矩阵
\\color{red}{伴随矩阵}”.

2. 逆矩阵公式的一个好处就是，我们从中可以看到，当改变原矩阵中的一个元素时，给逆矩阵带来了怎样的变化。

证明:
观察这个公式是如何运作的，化简公式得

ACT=(detA)I
AC^T=(\\det A)I，写成矩阵形式有

⎡⎣⎢⎢a11⋮an1a12⋮an2⋯⋱⋯a1n⋮ann⎤⎦⎥⎥⎡⎣⎢⎢⎢⎢⎢C11C12⋮C1n⋯⋯⋱⋯Cn1Cn2⋮Cnn⎤⎦⎥⎥⎥⎥⎥=Res
\\begin{bmatrix}a_{11}& a_{12}& \\cdots& a_{1n}\\\\\\vdots& \\vdots& \\ddots& \\vdots\\\\a_{n1}& a_{n2}& \\cdots& a_{nn}\\end{bmatrix}\\begin{bmatrix}C_{11}& \\cdots& C_{n1}\\\\C_{12}& \\cdots& C_{n2}\\\\\\vdots& \\ddots& \\vdots\\\\C_{1n}& \\cdots& C_{nn}\\end{bmatrix}=Res
对于这两个矩阵的乘积，观察其结果的元素

Res11=a11C11+a12C12+⋯+a1nC1n
Res_{11}=a_{11}C_{11}+a_{12}C_{12}+\\cdots+a_{1n}C_{1n}，这正是上一讲提到的将行列式按第一行展开的结果。同理，对

Res22,⋯,Resnn
Res_{22}, \\cdots, Res_{nn}都有

Resii=detA
Res_{ii}=\\det A，即对角线元素均为

detA
\\det A。
再来看非对角线元素：回顾二阶的情况，如果用第一行乘以第二行的代数余子式

a11C21+a12C22
a_{11}C_{21}+a_{12}C_{22}，得到

a(−b)+ab=0
a(-b)+ab=0。换一种角度看问题，

a(−b)+ab=0
a(-b)+ab=0也是一个矩阵的行列式值，即

As=[aabb]
A_{s}=\\begin{bmatrix}a& b\\\\a& b\\end{bmatrix}。将

detAs
\\det A_{s}按第二行展开，也会得到

detAs=a(−b)+ab
\\det A_{s}=a(-b)+ab，因为行列式有两行相等所以行列式值为零。
推广到

n
n阶，我们来看元素Res1n=a11Cn1+a12Cn2+⋯+a1nCnnRes_{1n}=a_{11}C_{n1}+a_{12}C_{n2}+\\cdots+a_{1n}C_{nn}，该元素是第一行与最后一行的代数余子式相乘之积。这个式子也可以写成一个特殊矩阵的行列式，即矩阵

As=⎡⎣⎢⎢⎢⎢⎢⎢⎢a11a21⋮an−a1a11a12a22⋮an−12a12⋯⋯⋱⋯⋯a1na2n⋮an−1na1n⎤⎦⎥⎥⎥⎥⎥⎥⎥
A_{s}=\\begin{bmatrix}a_{11}& a_{12}& \\cdots& a_{1n}\\\\a_{21}& a_{22}& \\cdots& a_{2n}\\\\\\vdots& \\vdots& \\ddots& \\vdots\\\\a_{n-a1}& a_{n-12}& \\cdots& a_{n-1n}\\\\a_{11}& a_{12}& \\cdots& a_{1n}\\end{bmatrix}。计算此矩阵的行列式，将

detAs
\\det A_{s}按最后一行展开，也得到

detAs=a11Cn1+a12Cn2+⋯+a1nCnn
\\det A_{s}=a_{11}C_{n1}+a_{12}C_{n2}+\\cdots+a_{1n}C_{nn}。同理，行列式

As
A_{s}有两行相等，其值为零。
结合对角线元素与非对角线元素的结果，我们得到

Res=⎡⎣⎢⎢⎢⎢⎢detA0⋮00detA⋮0⋯⋯⋱⋯00⋮detA⎤⎦⎥⎥⎥⎥⎥
Res=\\begin{bmatrix}\\det A& 0& \\cdots& 0\\\\0& \\det A& \\cdots& 0\\\\\\vdots& \\vdots& \\ddots& \\vdots\\\\0& 0& \\cdots& \\det A\\end{bmatrix}，也就是

(1)
(1)等式右边的

(detA)I
(\\det A)I，得证。

2.求解

Ax=b
Ax=b

---

因为我们现在有了逆矩阵的计算公式，所以对

Ax=b
Ax=b有

x=A−1b=1detACTb
x=A^{-1}b=\\frac{1}{\\det A}C^Tb，这就是计算

x
x的公式，即克莱默法则（Cramer’s rule）。即

克莱默法则\\color{red}{克莱默法则}:
1. 定义:对于可逆矩阵

A
A，方程Ax=bAx=b必然有解

x=A−1b
x=A^{-1}b，将逆矩阵公式代入有：

x=1detACTb
x=\\frac{1}{\\det A}C^Tb。
2. 克莱默法则从另外一个角度来看，实际上

x
x的分量为：
xi=detBidetAx_i=\\frac{\\det B_i}{\\det A}
其中矩阵

Bi
B_i是向量

b
b替代矩阵AA的第

j
j列所得到的新矩阵。

对2进行解析:

现在来观察x=1detACTbx=\\frac{1}{\\det A}C^Tb，我们将得到的解拆分开来，对

x
x的第一个分量有x1=y1detAx_1=\\frac{y_1}{\\det A}，这里

y1
y_1是一个数字，其值为

y1=b1C11+b2C21+⋯+bnCn1
y_1=b_1C_{11}+b_2C_{21}+\\cdots+b_nC_{n1}，每当我们看到数字与代数余子式乘之积求和时，都应该联想到求行列式，也就是说

y1
y_1可以看做是一个矩阵的行列式，我们设这个矩阵为

B1
B_1。所以有

xi=detB1detA
x_i=\\frac{\\det B_1}{\\det A}，同理有

x2=detB2detA
x_2=\\frac{\\det B_2}{\\det A}，

x3=detB3detA
x_3=\\frac{\\det B_3}{\\det A}。
而

B1
B_1是一个型为

[ba2a3⋯an]
\\Bigg[b a_2 a_3 \\cdots a_n\\Bigg]的矩阵，即将矩阵

A
A的第一列变为bb向量而得到的新矩阵。其实很容易看出，

detB1
\\det B_1可以沿第一列展开得到

y1=b1C11+b2C21+⋯+bnCn1
y_1=b_1C_{11}+b_2C_{21}+\\cdots+b_nC_{n1}。
一般的，有

Bj=[a1a2⋯aj−1baj+1⋯an]
B_j=\\Bigg[a_1 a_2 \\cdots a_{j-1} b a_{j+1} \\cdots a_n\\Bigg]，即将矩阵

A
A的第jj列变为

b
b向量而得到的新矩阵。所以，对于解的分量有xi=detBidetAx_i=\\frac{\\det B_i}{\\det A}。

这个公式虽然很漂亮，但是并不方便计算。因为：

detB1=b1C11+b2C21+⋯+bnCn1
\\det B_1=b_1C_{11}+b_2C_{21}+\\cdots+b_nC_{n1}使列向量

CTb
C^Tb的第一个分量，也对应为列向量

x
x的第一个分量。
矩阵BjB_j的行列式的数值是伴随矩阵

CT
C_T的第

j
j 行与向量

b
b 点积的结果。此处我们用到了行列式的性质10。相比于消元法，采用克莱姆法则计算方程的解效率较低。所以克莱姆法则计算量太大，不适合编程，消元法可以很好的解决问题，matlab就是用消元法来求解的。

3.行列式的几何意义——体积（Volume）

---

三阶矩阵A 行列式的绝对值等于以矩阵A 行（列）向量为边所构成的平行六面体的体积。行列式的正负对应左手系和右手系。之前提到过行列式是将矩阵的信息压缩成一个数，可以将“体积”视为它压缩后给出的信息。

1. 先提出命题：行列式的绝对值等于一个箱子的体积。
   来看三维空间中的情形，对于

   3
   3阶方阵AA，取第一行

   (a1,a2,a3)
   (a_1,a_2,a_3)，令其为三维空间中点

   A1
   A_1的坐标，同理有点

   A2,A3
   A_2, A_3。连接这三个点与原点可以得到三条边，使用这三条边展开得到一个平行六面体，

   ∥detA∥
   \\left\\|\\det A\\right\\|就是该平行六面体的体积。

2. 对于三阶单位矩阵，其体积为

   detI=1
   \\det I=1，此时这个箱子是一个单位立方体。这其实也证明了前面学过的行列式性质1。

3. 于是我们想，如果能接着证明性质2、3即可证明体积与行列式的关系。
   对于行列式性质2，我们交换两行并不会改变箱子的大小，同时行列式的绝对值也没有改变，得证。
   1) 现在我们取矩阵

   A=Q
   A=Q，而

   Q
   Q是一个标准正交矩阵，此时这个箱子是一个立方体，可以看出其实这个箱子就是刚才的单位立方体经过旋转得到的。对于标准正交矩阵，有QTQ=IQ^TQ=I，等式两边取行列式得

   det(QTQ)=1=∣∣QT∣∣|Q|
   \\det(Q^TQ)=1=\\left|Q^T\\right|\\left|Q\\right|，而根据行列式性质10有

   ∣∣QT∣∣=|Q|
   \\left|Q^T\\right|=\\left|Q\\right|，所以

   原式=|Q|2=1,|Q|=±1
   原式=\\left|Q\\right|^2=1, \\left|Q\\right|=\\pm 1。
   2) 接下来在考虑不再是“单位”的立方体，即长方体。 假设

   Q
   Q矩阵的第一行翻倍得到新矩阵Q2Q_2，此时箱子变为在第一行方向上增加一倍的长方体箱子，也就是两个“标准正交箱子”在第一行方向上的堆叠。易知这个长方体箱子是原来体积的两倍，而根据行列式性质3.a有

   detQ2=detQ
   \\det Q_2=\\det Q，于是体积也符合行列式的数乘性质。

二阶行列式是平行四边形的面积 。

1. 我们来看二阶方阵的情形，

   ∣∣∣a+a′cb+b′d∣∣∣=∣∣∣acbd∣∣∣+∣∣∣a′cb′d∣∣∣
   \\begin{vmatrix}a+a\’& b+b\’\\\\c& d\\end{vmatrix}=\\begin{vmatrix}a& b\\\\c& d\\end{vmatrix}+\\begin{vmatrix}a\’& b\’\\\\c& d\\end{vmatrix}。在二阶情况中，行列式就是一个求平行四边形面积的公式，原来我们求由四个点

   (0,0),(a,b),(c,d),(a+c,b+d)
   (0,0), (a,b), (c,d), (a+c,b+d)围成的四边形的面积，需要先求四边形的底边长，再做高求解，现在只需要计算

   detA=ad−bc
   \\det A=ad-bc即可（更加常用的是求由

   (0,0),(a,b),(c,d)
   (0,0), (a,b), (c,d)围成的三角形的面积，即

   12ad−bc
   \\frac{1}{2}ad-bc）。
   2.
   

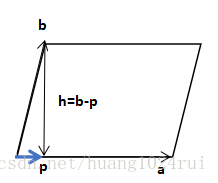
即：如果知道了歪箱子的顶点坐标，求面积（二阶情形）或体积（三阶情形）时，我们不再需要开方、求角度，只需要计算行列式的值就行了。

再多说两句我们通过好几讲得到的这个公式，在一般情形下，由点

(x1,y1),(x2,y2),(x3,y3)
(x_1,y_1), (x_2,y_2), (x_3,y_3)围成的三角形面积等于

12∣∣∣∣∣x1x2x3y1y2y3111∣∣∣∣∣
\\frac{1}{2}\\begin{vmatrix}x_1& y_1& 1\\\\x_2& y_2& 1\\\\x_3& y_3& 1\\end{vmatrix}，计算时分别用第二行、第三行减去第一行化简到第三列只有一个

1
1（这个操作实际作用是将三角形移动到原点），得到12∣∣∣∣∣x1x2−x1x3−x1y1y2−y1y3−y1100∣∣∣∣∣\\frac{1}{2}\\begin{vmatrix}x_1& y_1& 1\\\\x_2-x_1& y_2-y_1& 0\\\\x_3-x_1& y_3-y_1& 0\\end{vmatrix}，再按照第三列展开，得到三角形面积等于

(x2−x1)(y3−y1)−(x3−x1)(y2−y1)2
\\frac{(x_2-x_1)(y_3-y_1)-(x_3-x_1)(y_2-y_1)}{2}。

4.总结

---

1.矩阵的逆

A−1=1detACT
A^{-1}=\\frac{1}{\\det A}C^T

2.

克莱默法则
\\color{red}{克莱默法则}:
1. 定义:对于可逆矩阵

A
A，方程Ax=bAx=b必然有解

x=A−1b
x=A^{-1}b，将逆矩阵公式代入有：

x=1detACTb
x=\\frac{1}{\\det A}C^Tb。
2. 克莱默法则从另外一个角度来看，实际上

x
x的分量为：
xi=detBidetAx_i=\\frac{\\det B_i}{\\det A}
其中矩阵

Bi
B_i是向量

b
b替代矩阵AA的第

j
j列所得到的新矩阵。

3.行列式的几何意义：2维为平行四边形面积，3维为立方体的面积。

---

第二十一讲：特征值和特征向量

---

1.特征值、特征向量的由来

给定矩阵AA，矩阵

A
A乘以向量xx，就像是使用矩阵

A
A作用在向量xx上，最后得到新的向量

Ax
Ax。在这里，矩阵

A
A就像是一个函数，接受一个向量xx作为输入，给出向量

Ax
Ax作为输出。

在这一过程中，我们对一些特殊的向量很感兴趣，他们在输入(

x
x)输出(AxAx)的过程中始终保持同一个方向，这是比较特殊的，因为在大多情况下，

Ax
Ax与

x
x指向不同的方向。

在这种特殊的情况下，AxAx平行于

x
x，我们把满足这个条件的xx成为

特征向量
\\color{red}{特征向量}（Eigen vector）,而

λ
λ为AA 的

特征值
\\color{red}{特征值} 。这个平行条件用方程表示就是：

Ax=λx(1)

Ax=\\lambda x\\tag{1}

• 对这个式子，我们试着计算特征值为

  0
  0的特征向量，此时有Ax=0Ax=0，也就是特征值为

  0
  0的特征向量应该位于AA的零空间中。

矩阵是奇异的，那么它将有一个特征值为λ=0
\\color{red}{ 矩阵是奇异的，那么它将有一个特征值为\\lambda = 0}。

• 我们再来看投影矩阵

  P=A(ATA)−1AT
  P=A(A^TA)^{-1}A^T的特征值和特征向量。
  

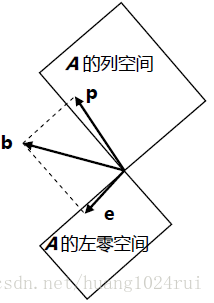
  1. 用向量

     b
     b乘以投影矩阵PP得到投影向量

     Pb
     Pb，在这个过程中，只有当

     b
     b已经处于投影平面（即AA的列空间）中时，

     Pb
     Pb与

     b
     b才是同向的，此时bb投影前后不变（

     Pb=1⋅b
     Pb=1\\cdot
     b）。即在投影平面中的所有向量都是投影矩阵的特征向量，而他们的特征值均为1。

  2. 再来观察投影平面的法向量，也就是投影一讲中的

     e
     e向量。我们知道对于投影，因为e⊥C(A)e\\bot
     C(A)，所以

     Pe=0e
     Pe=0e，即特征向量e的特征值为0。

投影矩阵P=A(ATA)−1AT的特征值为λ=1,0
\\color{red}{投影矩阵P=A(A^TA)^{-1}A^T的特征值为\\lambda=1, 0}。

• 再多讲一个例子，二阶置换矩阵

  A=[0110]
  A=\\begin{bmatrix}0& 1\\\\1& 0\\end{bmatrix}，经过这个矩阵处理的向量，其元素会互相交换。即：交换向量

  [x1x2]
  [x_1 x_2]变为

  [x2x1]
  [x_2 x_1]的，即

  [x1x2]A=[x2x1]
  [x_1 x_2]A=[x_2 x_1]，

  x1,x2
  x_1,x_2为列向量，

  A
  A为列向量线性组合的系数。交换后的[x2x1][x_2 x_1]是初始向量

  [x1x2]
  [x_1 x_2]与一个因子的乘积。

  那么特征值为

  1
  1的特征向量（即经过矩阵交换元素前后仍然不变）应该型为[11]\\begin{bmatrix}1\\\\1\\end{bmatrix}。

  特征值为

  −1
  -1的特征向量（即经过矩阵交换元素前后方向相反）应该型为

  [1−1]
  \\begin{bmatrix}1\\\\-1\\end{bmatrix}。

从例三可得出特征值的性质：
1.对于一个

n×n
n\\times
n的矩阵，将会有

n
n个特征值，而这些特征值的和与该矩阵对角线元素的和相同，因此我们把矩阵对角线元素称为矩阵的迹（trace）。

∑i=1nλi=∑i=1naii

\\sum_{i=1}^n
\\lambda_i=\\sum_{i=1}^n a_{ii}
2.对称矩阵，其特征向量互相垂直。

根据前面学到的行列式的性质，则有置换矩阵、投影矩阵，矩阵越特殊，则我们得到的特征值与特征向量也越特殊。看置换矩阵中的特征值，两个实数1,−1，而且它们的特征向量是正交的。
\\color{red}{根据前面学到的行列式的性质，则有置换矩阵、投影矩阵，矩阵越特殊，则我们得到的特征值与特征向量也越特殊。看置换矩阵中的特征值，两个实数1, -1，而且它们的特征向量是正交的。}

在上面二阶转置矩阵的例子中，如果我们求得了一个特征值

1
1，那么利用迹的性质，我们就可以直接推出另一个特征值是−1-1。

证明2：
证明2：
对称矩阵的特征向量正交：

λ1
λ_1和

λ2
λ_2对是对称矩阵

（A=AT）
（A=A^T）的两个不同的特征值，对应的特征向量分别为

x1
x_1 和

x2
x_2 。则有

Ax1=λx1
Ax_1=λx_1，左乘

x2
x_2得

xT2Ax1=λ1xT2x1
x^T_2Ax_1=λ1x^T_2x_1。而又有

xT2Ax1=xT2ATx1=(Ax2)Tx1=(λ2x2)Tx1=λ2xT2x1
x^T_2Ax_1=x^T_2A^Tx_1=(Ax_2)^Tx_1=(λ_2x_2)^Tx_1=λ_2x^T_2x^1。因此有

(λ1−λ2)xT2x1=0
(λ_1−λ_2)x^T_2x_1=0，而两特征值不等，所以两特征向量正交。

2.求解

Ax=λx
Ax=\\lambda x

---

对于方程

Ax=λx
Ax=\\lambda x，有两个未知数，我们需要利用一些技巧从这一个方程中一次解出两个未知数，先移项得

(A−λI)x=0
(A-\\lambda I)x=0。

观察

(A−λI)x=0
(A-\\lambda I)x=0，右边的矩阵相当于将

A
A矩阵平移了λ\\lambda个单位，而如果方程有解，则这个平移后的矩阵

(A−λI)
(A-\\lambda I)一定是奇异矩阵，否则唯一的x必须为零向量，零向量是没有用的特征向量。

det(A−λI)=0(2)

\\det{(A-\\lambda{I})}=0\\tag{2}

这样一来，方程中就没有

x
x了，这个方程也叫作特征方程（characteristic equation）。有了特征值，代回(A−λI)x=0(A-\\lambda I)x=0，继续求

(A−λI)
(A-\\lambda I)的零空间即可。

2.1 例1

---

现在计算一个简单的例子，

A=[3113]
A=\\begin{bmatrix}3& 1\\\\1& 3\\end{bmatrix}。

则计算

det(A−λI)=∣∣∣3−λ113−λ∣∣∣
\\det{(A-\\lambda{I})}=\\begin{vmatrix}3-\\lambda& 1\\\\1& 3-\\lambda\\end{vmatrix}，也就是对角矩阵平移再取行列式。原式继续化简得

(3−λ)2−1=λ2−6λ+8=0,λ1=4,λ2=2
(3-\\lambda)^2-1=\\lambda^2-6\\lambda+8=0,
\\lambda_1=4,\\lambda_2=2。可以看到一次项系数

−6
-6与矩阵的迹有关，常数项与矩阵的行列式有关。

继续计算特征向量，

A−4I=[−111−1]
A-4I=\\begin{bmatrix}-1& 1\\\\1& -1\\end{bmatrix}，显然矩阵是奇异的（如果是非奇异说明特征值计算有误），解出矩阵的零空间

x1=[11]
x_1=\\begin{bmatrix}1\\\\1\\end{bmatrix}；同理计算另一个特征向量，

A−2I=[1111]
A-2I=\\begin{bmatrix}1& 1\\\\1& 1\\end{bmatrix}，解出矩阵的零空间

x2=[1−1]
x_2=\\begin{bmatrix}1\\\\-1\\end{bmatrix}。

回顾前面转置矩阵的例子，对矩阵

A′=[0110]
A\’=\\begin{bmatrix}0& 1\\\\1& 0\\end{bmatrix}有

λ1=1,x1=[11],λ2=−1,x2=[−11]
\\lambda_1=1, x_1=\\begin{bmatrix}1\\\\1\\end{bmatrix}, \\lambda_2=-1, x_2=\\begin{bmatrix}-1\\\\1\\end{bmatrix}。

看转置矩阵

A′
A\’与本例中的对称矩阵

A
A有什么联系。

易得A=A′+3IA=A\’+3I，两个矩阵特征值相同，而其特征值刚好相差

3
3。也就是如果给一个矩阵加上3I3I，则它的特征值会加

3
3，而特征向量不变。

所以可以得出结论：
1. 如果Ax=λxAx=\\lambda x，则

(A+3I)x=λx+3x=(λ+3)x
(A+3I)x=\\lambda x+3x=(\\lambda+3)x，所以

x
x还是原来的xx，而

λ
\\lambda变为

λ+3
\\lambda+3。
2. 特征值之和等于矩阵的迹；特征值之积等于矩阵的行列式。

∏i=1nλi=detA

\\prod_{i=1}^n\\lambda_i=\\det A
3. 关于特征向量认识的误区：已知

Ax=λx,Bx=αx
Ax=\\lambda x, Bx=\\alpha x，则有

(A+B)x=(λ+α)x
(A+B)x=(\\lambda+\\alpha)x，当

B=3I
B=3I时，在上例中我们看到，确实成立，但是如果

B
B为任意矩阵，则推论不成立，因为这两个式子中的特征向量xx并不一定相同，所以两个式子的通常情况是

Ax=λx,By=αy
Ax=\\lambda x, By=\\alpha y，它们也就无从相加了。

证明2：
在例1中有：

det(A)=λ2−6λ+8=λ2−trace(A)λ+det(A)
det(A) = \\lambda^2-6\\lambda+8 =\\lambda^2-trace(A)\\lambda+det(A) 矩阵的迹等于特征值之和。
将

det（A−λI）=0
det（A−λI）=0展开会得到

λ
λ的nn阶多项式，多项式的解就是矩阵

A
A 的特征值。 根据多项式根与系数的关系，解之和（即特征值之和）等于

λn−1
λ^{n−1 }的系数。举例一元二次方程

ax2+bx+c
ax^2+bx+c之求根公式是

x1,2=−b±b2−4ac√2a
x_{1,2}=\\frac{−b\\pm\\sqrt{b^2-4ac}}{2a}，解之和

x1+x2=−ba
x_1+x_2=\\frac{−b}{a}，其中

a=1
a=1，所以解之和为

−b
−b。
而行列式展开式（n阶多项式）中只有对角线的积这一项包含的

λn−1
λ^{n−1}（其它项最高是

n−2
n-2 次方），而其系数为矩阵A 的迹。因此特征值之和与矩阵的迹相等。

2.2例2

---

再来看旋转矩阵的例子，旋转

90∘
90^\\circ的矩阵

Q=[cos90sin90−sin90cos90]=[01−10]
Q=\\begin{bmatrix}\\cos {90}& -\\sin
{90}\\\\sin {90}& \\cos
{90}\\end{bmatrix}=\\begin{bmatrix}0& -1\\\\1& 0\\end{bmatrix}（将每个向量旋转

90∘
90^\\circ，用

Q
Q表示因为旋转矩阵是正交矩阵中很重要的例子）。

根据上面提到特征值的一个性质：特征值之和等于矩阵的迹和特征值之积等于矩阵的行列式。则对于QQ矩阵，有

{λ1+λ2λ1⋅λ2=0=1
\\begin{cases}\\lambda_1+\\lambda_2& =0\\\\\\lambda_1\\cdot\\lambda_2& =1\\end{cases}，再来思考特征值与特征向量的由来，哪些向量旋转

90∘
90^\\circ后与自己平行，于是遇到了麻烦，并没有这种向量，也没有这样的特征值来满足前面的方程组。

我们来按部就班的计算，

det(Q−λI)=∣∣∣λ1−1λ∣∣∣=λ2+1=0
\\det(Q-\\lambda I)=\\begin{vmatrix}\\lambda& -1\\\\1& \\lambda\\end{vmatrix}=\\lambda^2+1=0，于是特征值为

λ1=i,λ2=−i
\\lambda_1=i, \\lambda_2=-i，我们看到这两个值满足迹与行列式的方程组，即使矩阵全是实数，其特征值也可能不是实数，本例中即出现了一对共轭负数。

我们可以说：
1.如果矩阵越接近对称，那么特征值就是实数。如果矩阵越不对称，就像本例，

QT=−Q
Q^T=-Q，这是一个反对称的矩阵，于是我得到了纯虚的特征值，这是极端情况，通常我们见到的矩阵是介于对称与反对称之间的。
2.实数特征值让特征向量伸缩而虚数让其旋转。

于是我们看到，对于好的矩阵（置换矩阵）有实特征值及正交的特征向量，对于不好的矩阵（

90∘
90^\\circ旋转矩阵）有纯虚的特征值。

2.3例3

---

再来看一个更糟的情况，

A=[3013]
A=\\begin{bmatrix}3& 1\\\\0& 3\\end{bmatrix}，这是一个三角矩阵，我们可以直接得出其特征值，即对角线元素。来看如何得到这一结论的：

det(A−λI)=∣∣∣3−λ013−λ∣∣∣=(3−λ)2=0
\\det(A-\\lambda
I)=\\begin{vmatrix}3-\\lambda& 1\\\\0& 3-\\lambda\\end{vmatrix}=(3-\\lambda)^2=0，于是

λ1=3,λ2=3
\\lambda_1=3,
\\lambda_2=3。而我们说这是一个糟糕的状况，在于它的特征向量。

带入特征值计算特征向量，带入

λ1=3
\\lambda_1=3得

(A−λI)x=[0010][x1x2]=[00]
(A-\\lambda I)x=\\begin{bmatrix}0& 1\\\\0& 0\\end{bmatrix}\\begin{bmatrix}x_1\\\\x_2\\end{bmatrix}=\\begin{bmatrix}0\\\\0\\end{bmatrix}，算出一个特征值

x1=[10]
x_1=\\begin{bmatrix}1\\\\0\\end{bmatrix}，当我们带入第二个特征值

λ1=3
\\lambda_1=3时，我们无法得到另一个与

x1
x_1线性无关的特征向量了。

而本例中的矩阵

A
<script type="math/tex" id="MathJax-Element-20032">A</script>是一个退化矩阵（degenerate matrix）。

一个退化矩阵，重复的特征值在特殊情况下可能导致特征向量的短缺。

这一讲我们看到了足够多的“不好”的矩阵，下一讲会介绍一般情况下的特征值与特征向量。

3. 总结

---

1.特征向量和特征值的由来；
2.3个例子得出的结论（对称矩阵、旋转矩阵、三角矩阵的特征值与特征向量的特点）。